高考数学复习练习试题10_3变量的相关性 5页

‎§10.3　变量的相关性 一、填空题(本大题共9小题，每小题6分，共54分)‎ ‎1．下列关系中，具有相关关系的为______．(填序号)‎ ‎①学生的学习态度与学习成绩之间的关系；‎ ‎②教师的执教水平与学生的学习成绩之间的关系；‎ ‎③学生的身高与学生的学习成绩之间的关系；‎ ‎④家庭的经济条件与学生的学习成绩之间的关系．‎ ‎2．已知变量x，y呈线性相关关系，回归方程为 ＝0.5＋2x，则变量x，y的相关关系是________相关．(填“正”、“负”)‎ ‎3．(2010·广州模拟)工人月工资(元)依劳动产值(千元)变化的回归直线方程为 ＝60＋90x，则下列判断正确的是________．(填序号)‎ ‎①劳动产值为1 000元时，工资为50元 ‎②劳动产值提高1 000元时，工资提高150元 ‎③劳动产值提高1 000元时，工资提高90元 ‎④劳动产值为1 000元时，工资为90元 ‎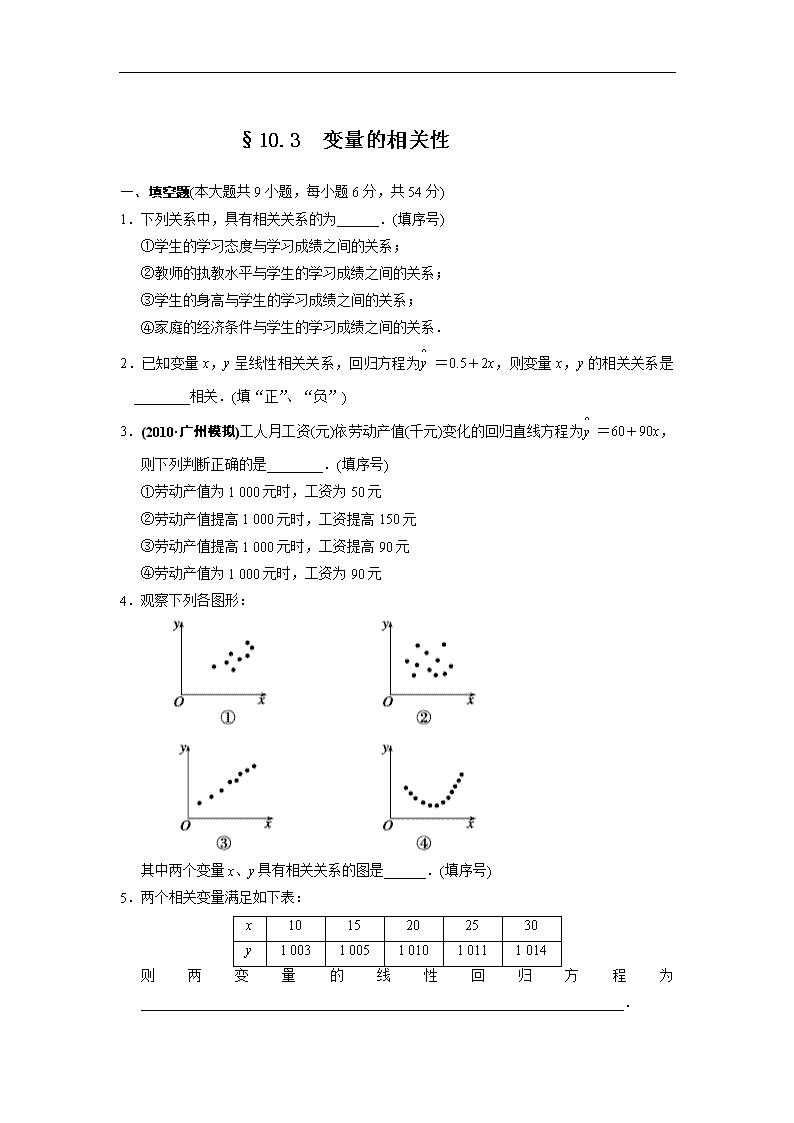4．观察下列各图形：‎ 其中两个变量x、y具有相关关系的图是______．(填序号)‎ ‎5．两个相关变量满足如下表：‎ x ‎10‎ ‎15‎ ‎20‎ ‎25‎ ‎30‎ y ‎1 003‎ ‎1 005‎ ‎1 010‎ ‎1 011‎ ‎1 014‎ 则两变量的线性回归方程为_____________________________________________________________________．‎ ‎6．(2010·盐城期末)某单位为了了解用电量y度与气温x℃之间的关系，随机统计了某4天的用电量与当天气温，并制作了对照表：‎ 气温(℃)‎ ‎18‎ ‎13‎ ‎10‎ ‎－1‎ 用电量(度)‎ ‎24‎ ‎34‎ ‎38‎ ‎64‎ 由表中数据得线性回归方程 ＝ x＋ 中 ＝－2，预测当气温为－‎4℃‎时，用电量的度数约为______．‎ ‎7．某服装商场为了了解毛衣的月销售量y(件)与月平均气温x(℃)之间的关系，随机统计了4 个月的月销售量与当月平均气温，其数据如下表：‎ 月平均气温x(℃)‎ ‎17‎ ‎13‎ ‎8‎ ‎2‎ 月销售量y(件)‎ ‎24‎ ‎33‎ ‎40‎ ‎55‎ 由表中数据算出线性回归方程 ＝ x＋ 中的 ≈－2.气象部门预测下个月毛衣的销售量约为________件．‎ ‎8．已知三点(3,10)，(7,20)，(11,24)的横坐标x与纵坐标y具有线性相关关系，则其线性回归方程是________________．‎ ‎9．下表是某厂1～4月份用水量(单位：百吨)的一组数据，‎ 月份x ‎1‎ ‎2‎ ‎3‎ ‎4‎ 用水量y ‎4.5‎ ‎4‎ ‎3‎ ‎2.5‎ 由其散点图可知，用水量y与月份x之间有较好的线性相关关系，其线性回归方程是 ＝－0.7x＋ ，则 ＝________.‎ 二、解答题(本大题共3小题，共46分)‎ ‎10．(14分)在某地区的12～30岁居民中随机抽取了10个人的身高和体重的统计资料如表：‎ 身高(cm)‎ ‎143‎ ‎156‎ ‎159‎ ‎172‎ ‎165‎ ‎171‎ ‎177‎ ‎161‎ ‎164‎ ‎160‎ 体重(kg)‎ ‎41‎ ‎49‎ ‎61‎ ‎79‎ ‎68‎ ‎69‎ ‎74‎ ‎69‎ ‎68‎ ‎54‎ 根据上述数据，画出散点图并判断居民的身高和体重之间是否有相关关系．‎ ‎11．(16分)(2010·扬州模拟)为了分析某个高三学生的学习状态，对其下一阶段的学习提供指导性建议．现对他前7次考试的数学成绩x、物理成绩y进行分析．下面是该生7次考试的成绩：‎ 数学 ‎88‎ ‎83‎ ‎117‎ ‎92‎ ‎108‎ ‎100‎ ‎112‎ 物理 ‎94‎ ‎91‎ ‎108‎ ‎96‎ ‎104‎ ‎101‎ ‎106‎ ‎(1)他的数学成绩与物理成绩哪个更稳定？请给出你的证明；‎ ‎(2)已知该生的物理成绩y与数学成绩x是线性相关的，若该生的物理成绩达到115分，‎ 请你估计他的数学成绩大约是多少？并请你根据物理成绩与数学成绩的相关性，给出该生在学习数学、物理上的合理性建议．‎ ‎12．(16分)某电脑公司有6名产品推销员，其工作年限与年推销金额的数据如下表：‎ 推销员编号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 工作年限x/年 ‎3‎ ‎5‎ ‎6‎ ‎7‎ ‎9‎ 推销金额y/万元 ‎2‎ ‎3‎ ‎3‎ ‎4‎ ‎5‎ ‎(1)以工作年限为自变量x，推销金额为因变量y，作出散点图；‎ ‎(2)求年销售金额y关于工作年限x的线性回归方程；‎ ‎(3)若第6名推销员的工作年限为11年，试估计他的年推销金额．‎ 答案 ‎1．①② 2．正 3．③ 4．③④ 5. ＝0.56x＋997.4‎ ‎6．68 7．46 8. ＝x＋ 9．5.25‎ ‎10 解　以x轴表示身高，y轴表示体重，可得到相应的散点图如图所示：‎ 由散点图可知，两者之间具有相关关系，且为正相关．‎ ‎11．解　(1)＝100＋＝100；‎ ＝100＋＝100；‎ ‎∴s＝＝142，∴s＝，‎ 从而s>s，∴物理成绩更稳定．‎ ‎(2)由于x与y之间具有线性相关关系，根据回归系数公式得到 ＝＝＝0.5，‎ ＝－ ＝100－0.5×100＝50，‎ ‎∴线性回归方程为 ＝0.5x＋50.‎ 当y＝115时，x＝130，即该生物理成绩达到115分时，他的数学成绩大约为130分．‎ 建议：进一步加强对数学的学习，提高数学成绩的稳定性，将有助于物理成绩的进一步 提高．‎ ‎12．解　(1)依题意，画出散点图如图所示，‎ ‎ (2)从散点图可以看出，这些点大致在一条直线附近，设所求的线性回归方程为 ＝ x＋ ，‎ 则 ＝＝＝0.5， ＝－ ＝0.4，‎ ‎∴年推销金额y关于工作年限x的线性回归方程为 ＝0.5x＋0.4.‎ ‎(3)由(2)可知，当x＝11时，‎ ＝0.5x＋0.4＝0.5×11＋0.4＝5.9(万元)．‎ ‎∴可以估计第6名推销员的年推销金额为5.9万元．‎