2019-2020学年江苏省常州市武进区礼嘉中学高一上学期期中考试数学试卷 10页

‎2019-2020学年江苏省常州市武进区礼嘉中学高一上学期期中考试数学试卷 注意事项：‎ ‎1．本试卷共4页，包括选择题（第1题～第12题）、填空题（第13题～第16题）、解答题（第17题～第22题）三部分。本试卷满分150分，考试时间120分钟。‎ ‎2．答题前，请务必将自己的姓名、考试号用毫米黑色签字笔填写在答题卡指定位置。‎ ‎3．答题时，必须用毫米黑色签字笔填写在答题卡的指定位置，在其它位置作答一律无效。‎ ‎4．如有作图需要，可用2B铅笔作答，并加黑加粗，描写清楚。‎ ‎5. 请保持答题卡卡面清洁，不要折叠、破损。不准使用胶带纸、修正液及可擦洗的圆珠笔。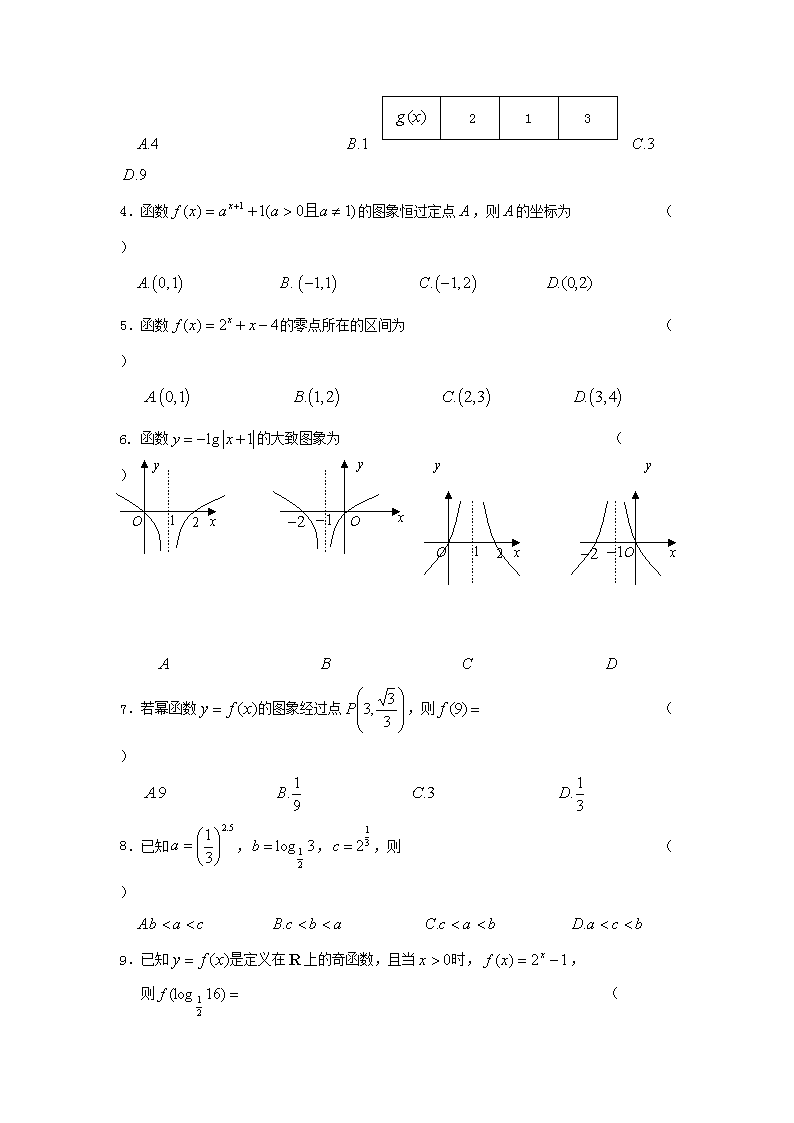‎ 一、选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，有一项是符合题目要求的.‎ ‎1．已知集合，，则的子集个数为 （ ） ‎ ‎ ‎ ‎2．函数的定义域为 （ ） ‎ ‎ ‎ ‎3． 已知函数与分别由下表给出，则 （ ） ‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎3‎ ‎9‎ ‎2‎ ‎3‎ ‎4‎ ‎2‎ ‎1‎ ‎3‎ ‎ ‎ ‎4．函数的图象恒过定点，则的坐标为 （ ） ‎ ‎ ‎ ‎5．函数的零点所在的区间为 （ ）‎ ‎ ‎ x O y y y x y ‎1‎ ‎2‎ O ‎6. 函数的大致图象为 （ ）‎ x ‎1‎ ‎2‎ O x O ‎ ‎ ‎7．若幂函数的图象经过点，则 （ ）‎ ‎ ‎ ‎8．已知，，，则 （ ）‎ ‎ ‎ ‎9．已知是定义在上的奇函数，且当时，，‎ 则 （ ）‎ ‎ ‎ ‎10.“弯弓射雕”描述了游牧民族的豪迈气概，当弓箭以每秒米的速度从地面垂直向上射箭时，秒时弓箭距地面的高度为米，可由确定. 已知射箭3秒时弓箭离地面高度为米，则弓箭能达到的最大高度为 （ ） ‎ ‎ ‎ 米 米 米 米 ‎11．已知函数的定义域为，对于任意的，都满足，且对于任意的，当时，都有，若，则实数的取值范围是 （ ） ‎ ‎ ‎ ‎ ‎ ‎12．已知函数，两者的定义域都是.若对于任意,存在，使得 且，则称为“兄弟函数”.已知函数， 是定义在区间上的“兄弟函数”，那么函数在区间上的最大值为 （ ） ‎ ‎ ‎ 二、填空题：本题共4小题，每小题5分，共20分.‎ ‎13．若集合， ，且，则实数的取值范围 为 .‎ ‎14．已知函数在上为偶函数，且时，则当时，‎ ‎ .‎ ‎15．已知函数在上是单调递增函数，则实数的取值范围是 ‎ .‎ ‎16．已知,函数若对于任意的，恒成立，则实数的取值范围是 . ‎ 三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.‎ ‎17.（本小题满分10分）‎ ‎（1）已知，化简：；‎ ‎（2）求值：.‎ ‎18. （本小题满分12分）‎ 设，.‎ ‎（1）若，求；‎ ‎（2）若，求实数的取值范围.‎ ‎19. （本小题满分12分）‎ ‎ 已知函数是奇函数.‎ ‎（1）求实数的值；‎ ‎（2）求证：函数在上是单调增函数.‎ ‎20.（本小题满分12分） ‎ 甲、乙两家鞋帽商场销售同一批品牌运动鞋，每双标价为元.甲、乙两商场销售方式如下：在甲商场买一双售价为元，买两双每双售价为元，依次类推，每多买一双则所买各双售价都再减少元，但每双售价不能低于元；乙商场一律按标价的销售.‎ ‎（1）分别写出在甲、乙两商场购买双运动鞋所需费用的函数解析式和.‎ ‎（2）某单位需购买一批此类品牌运动鞋作为员工福利，问：去哪家商场购买花费较少?‎ ‎21. （本小题满分12分）‎ ‎ 已知函数.‎ ‎（1）当时,作出函数的图象；‎ ‎（2）是否存在实数a，使得函数在区间 上有最小值8，若存在求出a的值；若不存在，请说明理由. ‎ ‎22. （本小题满分12分）‎ 对于定义域为的函数，如果存在区间，同时满足：‎ ‎①在内是单调函数；②当定义域是时，的值域也是，‎ 则称是该函数的“优美区间”．‎ ‎（1）求证：是函数的一个“优美区间”．‎ ‎（2）求证：函数不存在“优美区间”．‎ ‎（3）已知函数（）有“优美区间”，当变化时，求出的最大值．‎ ‎数学答案 一、选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，有一项是符合题目要求的.‎ ‎1. 2. 3. 4. 5. 6. ‎ ‎7. 8. 9. 10. 11. 12.‎ 二、填空题：本题共4小题，每小题5分，共20分.‎ ‎13. 14. 15. 16.‎ 三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.‎ ‎17．（本小题满分10分）‎ 解：（1） 又分 ‎ 分 分 ‎ ‎ 分 ‎（2）‎ ‎18．（本小题满分12分）‎ 解：（1） 分 ‎ 分 ‎ ‎ 分 ‎ （2）分 ‎ 分 ‎ ‎ 分 分 ‎19．（本小题满分12分）‎ ‎（1）法一：解：定义域为，是奇函数，‎ 对于定义域内的任意恒成立.‎ ‎ ‎ ‎，‎ 该式对于定义域中的任意都成立，即 法二：定义域为，是奇函数，，‎ ‎，解得 检验：当时，，定义域为关于原点对称，‎ 是奇函数. ‎ ‎（2）证明：在内任取，‎ 在上单调递增. ‎ ‎20．（本小题满分12分）‎ 解：（1）由可得当且时，去甲商场购买的单价为（）元，当且时，去甲商场购买的单价为元.去乙商场购买单价一直为元.‎ ‎ ‎ ‎ ‎ 注：（1）定义域中没有写总共扣1分.‎ ‎（2）如果学生写的是”且”也对.‎ ‎（2）当且时，；‎ ‎ 当且时，‎ ‎ 由解得且；‎ ‎ 由解得；‎ 由解得且 综上：当且时，；‎ ‎ 当时，；‎ 当且时，.‎ ‎ 答：（1） ，.‎ ‎（2）若单位购买少于双，去乙商场花费较少，若购买10双，则去两家商场花费相同，若购买超过10双，则去甲商场花费较少. ‎ ‎21. （本小题满分12分）‎ 解：（1）当时，‎ 分 注：图像弯曲细微有误扣1分，‎ 四个关键点有漏画总扣1分 ‎（2）假设存在实数，使得函数在区间上有最小值，‎ ‎ 当时，，‎ ‎ 对称轴方程为，在上单调递增 分 ‎ 当时，不可能有最小值（舍去）分 ‎ 当时，‎ 对称轴方程为，‎ ‎①当即时，‎ ‎，又舍去. 分 ‎②当即时，‎ ‎.‎ 综上：或.分 ‎22. （本小题满分12分）‎ 解：（1）在区间上单调递增．分 又，，值域为，‎ 区间是的一个“优美区间”.分 ‎（2）设是已知函数定义域的子集．，或，函数在上单调递减．分 若是已知函数的“优美区间”，则分 由得，‎ 代入等式不成立，函数不存在优美区间. 分 ‎（3）设是已知函数定义域的子集．，或，函数在上单调递增．分 若是已知函数的“优美区间”，则 分 ‎ ‎、是方程，即的两个同号且不等的实数根．‎ ‎，，同号，只须，‎ 即或分 ‎，分 当时，取最大值.分