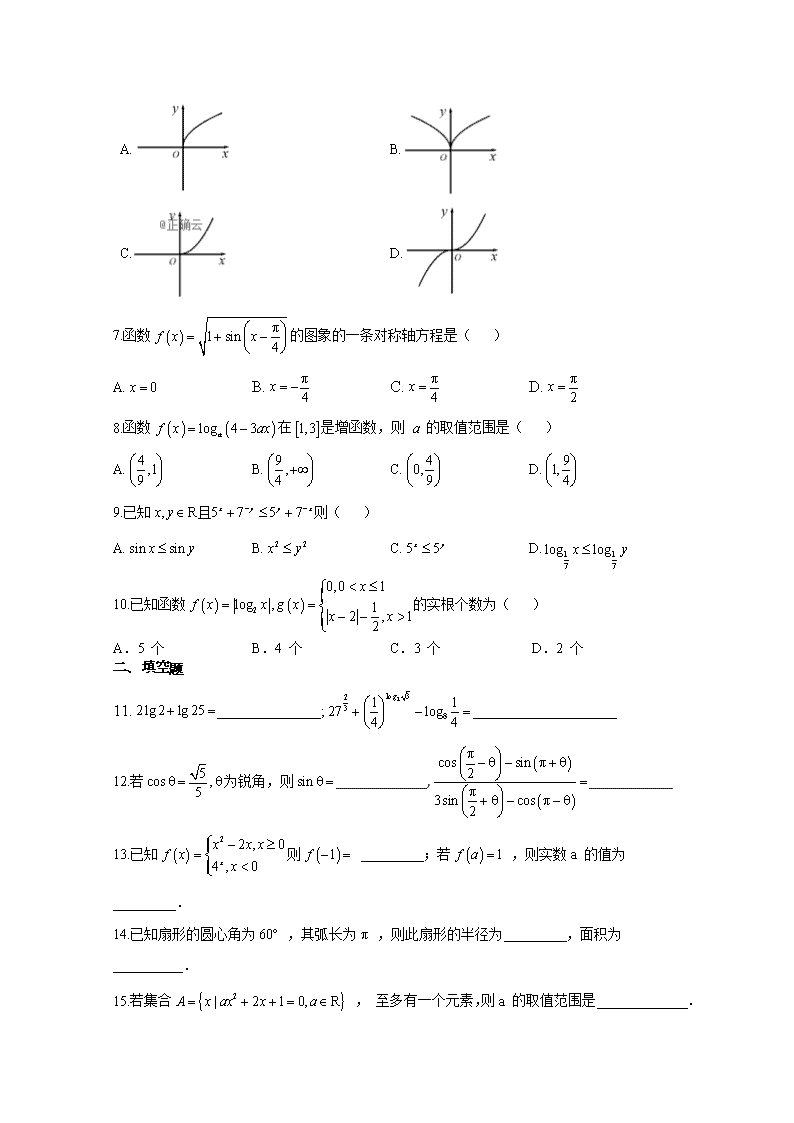黑龙江省绥化市安达市第七中学2019-2020学年高一下学期期末考试数学试卷 8页

数学试卷 一、选择题 1.已知集合    | 1 , | 0A x x B x x    则（ ） A.  | 0A B x x  B. RA B  C.  | 1A B x x  D. A B   2.下列函数中，与函数 y x 相同的是（ ） A. 11y x      B.  2 y x C. 2y x D. lg10xy  3.集合 π π| π π ,4 2k k k Z          中的角所表示的范围（阴影部分）是（ ） A. B. C. D. 4.函数   2log 2f x x  的零点是（ ） A. 3,0 B.3 C. 4,0 D.4 5.已知 0.8 1.2 12 , , ln 22a b c       则 , ,a b c 的大小关系为 （ ） A. c a b  B. c b a  C.b a c  D. b c a  6.已知函数    4 1 0, 0xf x a a a   且 的图象恒过定点 P ，若定点 P 在幂函数  g x 的图 象上，则幂函数 的图象是（ ） A. B. C. D. 7.函数   π1 sin 4f x x      的图象的一条对称轴方程是（ ） A. 0x  B. π 4x   C. π 4x  D. π 2x  8.函数      log 4 3af x ax  在 1,3 是增函数，则 a 的取值范围是（ ） A. 4 ,19      B. 9 ,4     C. 40, 9      D. 91, 4      9.已知 , R 5 7 5 7x y y xx y     且 则（ ） A. sin sinx y B. 2 2x y C. 5 5x y D. 1 1 7 7 log logx y 10.已知函数    2 0,0 1 log , 12 , 12 x f x x g x x x        的实根个数为（ ） A．5 个 B．4 个 C．3 个 D．2 个 二、填空题 11. 2lg 2 lg 25  _____________; 2log 32 3 8 1 127 log4 4       __________________ 12.若 5cos ,5    为锐角，则 sin   _____________,     πcos sin π2 π3sin cos π2                 ____________ 13.已知   2 2 , 0 4 , 0x x x xf x x      则  1f   _________；若   1f a  ，则实数 a 的值为 _________． 14.已知扇形的圆心角为 60 ，其弧长为 π ，则此扇形的半径为_________，面积为__________． 15.若集合  2| 2 1 0, RA x ax x a     ， 至多有一个元素，则 a 的取值范围是 _____________． 16.定义运算： , , b a ba b a a b     则函数   3 3x xf x   的值域为_________． 17.设函数   2 2 2f x x ax a    ，函数  g x ax a  ，若存在 0 Rx  ，使得  0 0f x  与  0 0g x  同时成立，则实数 a 的取值范围是_________ 三、解答题 18.已知集合  | 2 7A x x    ，  | 4 2 1B x m x m     ． （1）当 1m  时，求 A B ； （2）若集合 B 是集合 A 的子集，求实数 m 的取值范围． 19.已知函数   2 1 xf x x   的定义域为 1,1 ， （1）证明  f x 在  1,1 上是增函数； （2）解不等式    2 1 0f x f x   ． 20.已知函数     sin 0, 0, πf x A x A        ，在同一周期内，当 π 12x  时，  f x 取 得最大值 4；当 7π 12x  时，  f x 取得最小值 ． （1）求函数  f x 的解析式； （2）若 π π,6 6x      时，函数    2 1h x f x t   有两个零点，求实数 t 的取值范围 21.已知函数   1 11 2 4 x x f x a              ， （1）当 1a  时，求函数  f x 在  ,0 上的值域； （2）若不等式   3f x  对  0,x  恒成立，求实数 a 的取值范围． 22.已知函数  y f x 为偶函数，当 0x  时，   2 2 1f x x ax   （a 为常数）． （1）当 0x  时，求  f x 的解析式： （2）设函数  y f x 在 0,5 上的最大值为  g a ，求  g a 的表达式； （3）对于（2）中的  g a ，试求满足   18g g m      的所有实数 m 的取值集合. 参考答案 1.答案：A 解析：∵    1 ,| | 0A x x B x x    ， 则    0 ,| 1|A B x x A B x x     故选：A. 2.答案：D 解析： 3.答案：C 解析：当 2 , Zk n n  时， 2 24 2n n        ； 当 2 1, Zk n n   时， 2 24 2n n            . 故选 C. 4.答案：D 解析：由题意令 2log 2 0x   ，得 2log 2x  ，得 22 4x   所以函数   2log 2f x x  的零点是 4x  故选 D 5.答案：B 解析： 6.答案：A 解析： 7.答案：B 解析： 8.答案：C 解析： 9.答案：C 解析： 10.答案：B 解析： 11.答案：2;10 解析： 12.答案： 2 5 5 ;1 解析： 13.答案： 1 ;1 24  解析： 14.答案： 3π3; 2 解析： 15.答案： | 0 1a a a 或 解析： 16.答案： 0,1 解析： 17.答案： 1, 解析： 18.答案：（1）当 1m  时，  | 3 3B x x    ，∴  | 2 3A B x x    （2）由题意知 B A ， ① B   时， 4 2 1m m   ，∴  | 2 3A B x x    ② B   时， 5 4 2 2 1 7 m m m          ，∴ 2 3m  ∴m 的取值范围是    , 5 2,3   解析： 19.答案：（1）证明：设 1 21 1x x    ，则           1 2 1 21 2 1 2 2 2 2 2 1 2 1 2 1 1 1 1 1 x x x xx xf x f x x x x x         ∵ 1 21 1x x    ，∴ 1 2 0x x  ， 1 21 0x x  ，   2 2 1 21 1 0x x   ∴    1 2 0f x f x  ，即    1 2f x f x ，∴  f x 在  1,1 上是增函数. （2）  f x 显然为奇函数，∴由    2 1 0f x f x   得    2 1f x f x   ， ∴    2 1f x f x   ，由（1）知  f x 在  1,1 上是增函数，则 1 2 1 1 1 1 2 1 x x x x             ， 解得 10 3x  ，∴原不等式的解集 10, 3      解析： 20.答案：（1）由题意知 7π π π4, 2 12 12 2 TA     ，得周期 πT  ， 即 2π π 得 2  ，则    4sin 2f x x   当 π 12x  时，  f x 取得最大值 4，即 π4sin 2 412        ，得 πsin 16       ， 得 π π2 π6 2k    得 π2 π 3k   ∵ π  ，∴当 0k  时， π 3   ，即   π4sin 2 3f x x     。 （2）    2 1 0h x f x t    ，即   1 2 tf x  ， 当 π π,6 6x      时，则 π 2π2 0,3 3x       ， 当 π 2π2 3 3x   时， 2π4sin 2 33  ， 当 π π2 3 2x   时， π4sin 42  ， 要使   1 2 tf x  有两个根，则 12 3 42 t   ，得1 4 3 9t   即实数 t 的取值范围是1 4 3 9t   解析： 21.答案：（1） 1a  时，   1 11 2 4 x x f x             ，∵  f x 在 ,0 上递减， ∴    0f x f ，∴    3,f x   （2）   3f x  即   1 1 13 3 4 24 2 4 x x x f x a                        1 14 2 2 22 2 x x x xa                ∵ 12 2 2 x x       在 0, 上单调递增，∴ 12 2 12 x x       令      1 12 0 , 4.2 4 12 x x xt x y g x t tt                    所以    0 5g x g   ，由 1 14.2 2 22 2 x x x xa               恒成立， 得 5 1a   ，所以实数 a 的取值范围为 5,1 解析： 22.答案：（1）当 0x  时， 0x  ，又  y f x 为偶函数 ∴当 0x  时，        2 22 1 2 1f x f x x a x x ax           综上所述，结论是：   2 2 1f x x ax   ，  0x  （2）当 0a  时， 2 02 a a    ，  f x 在 0,5 上单调递增，    max 5 10 26f x f a   当 5a   时， 2 52 a a    ，  f x 在 0,5 上单调递减，    max 0 1f x f  当 55 2a    时， 2 5 ,52 2 a a        ，由抛物线对称性可知，    max 0 1f x f  当 5 2a   时， 2 5 2 2 a a    ，由抛物线对称性可知，      max 0 5 1f x f f   当 5 12 a   时， 2 50,2 2 a a        ，由抛物线对称性可知，    max 5 10 26f x f a   综上所述，结论是：   510 26, 2 51, 2 a a g a a         （3）由（2）知：   510 26, 2 51, 2 a a g a a         ，则   580 26, 168 51, 16 m m g m m         ， 10 1 526,1 2 1 51, 2 m mg m m             即  10 226, , 0,51 21, ,05 mmg m m                        ， 由   18g m g m      ，得： 当  0,m  时，有 1080 26 26m m    ，即 2 1 8m  ，所以 2 4m  ； 当 5 ,016m      时，有80 26 1m   ，解得： 5 5 ,016 16m        ，舍去； 当 2 5,5 16m       时，   18 1g m g m      ，故 2 5,5 16m       ； 当 2, 5m       时， 101 26m   ，解得： 2 2,5 5m         ; 综上得：满足   18g m g m      的所有实数的取值集合为 2 5 2,5 16 4              综上所述，结论是：满足   18g m g m      的所有实数的取值集合为 2 5 2,5 16 4              解析：