数学（理）卷·2017届黑龙江省哈六中高三上学期期末考试（2017 10页

哈尔滨市第六中学2016-2017学年度上学期期末考试 高三理科数学 一、选择题（共12小题，每题5分，共60分）‎ ‎1．复数等于（ ）‎ A. B. C. D.0‎ ‎2．等比数列中，，前3项和为，则公比的值是（ ）‎ A. 1 B.－ C. 1或－ D. -1或－‎ ‎3. 已知，则（ ）‎ ‎ A. B. C. D. ‎ ‎4．已知满足不等式组，则的最大值与最小值的比值为( )‎ A. B. C. D.‎ ‎5．下列选项中，说法正确的个数是( )‎ ‎(1)命题“，”的否定为“”；‎ ‎(2)命题“在中，，则”的逆否命题为真命题；‎ ‎(3)设是公比为的等比数列，则“”是“为递增数列”的充分必要条件；‎ ‎(4)若统计数据的方差为1,则的方差为2；‎ ‎(5)若两个随机变量的线性相关性越强,则相关系数绝对值越接近1.‎ ‎ A.1个 B.2个 C.3个 D.4个 ‎6. 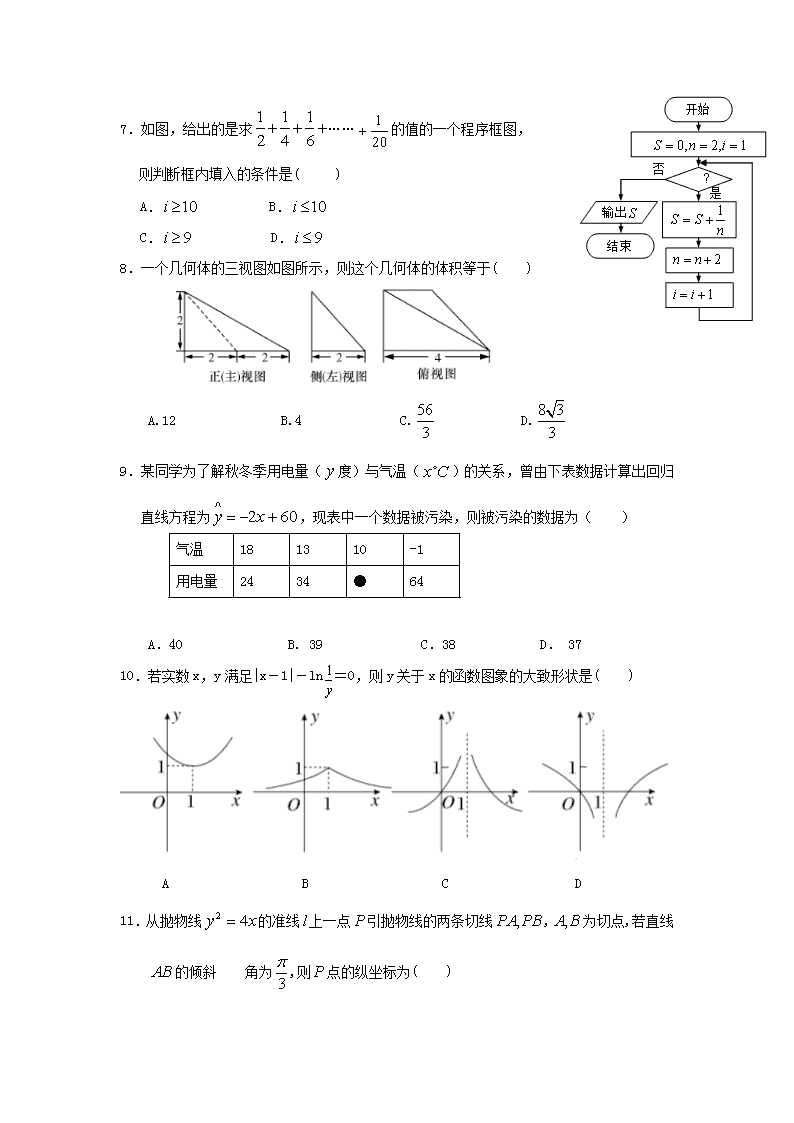某校组织由5名学生参加的演讲比赛，采用抽签法决定演讲顺序，在“学生和都不是第一个出场，不是最后一个出场”的前提下，学生第一个出场的概率为（ ）‎ A． B． C． D．‎ ‎?‎ ‎7．如图，给出的是求……的值的一个程序框图，‎ 则判断框内填入的条件是( )‎ A． B． ‎ C． D．‎ ‎8．一个几何体的三视图如图所示，则这个几何体的体积等于( ) ‎ ‎ A.12 B.4 C. D.‎ ‎9．某同学为了解秋冬季用电量（度）与气温（）的关系，曾由下表数据计算出回归直线方程为，现表中一个数据被污染，则被污染的数据为（ ）‎ 气温 ‎18‎ ‎13‎ ‎10‎ ‎-1‎ 用电量 ‎24‎ ‎34‎ ‎●‎ ‎64‎ A．40 B. 39 C．38 D． 37‎ 10． 若实数x，y满足|x－1|－ln＝0，则y关于x的函数图象的大致形状是(　　)‎ A B C D 11． 从抛物线的准线上一点引抛物线的两条切线,为切点,若直线的倾斜 角为,则点的纵坐标为( )‎ A. B. C. D. ‎ ‎12. 若方程有四个不同的实数根，且则的取值范围是（ ）‎ A. B. C. D.‎ 二、填空题：（共4题，每题5分，共20分）‎ ‎13．在的二项展开式中，的系数为 .‎ ‎14. 在直三棱柱中，侧棱长为，在底面中，，则此直三 棱柱的外接球的表面积为 .‎ ‎15．已知点分别是双曲线的左、右焦点，过的直线与双曲线的左、右两支分别交于两点，若，则双曲线的离心率为 .‎ ‎16.中，边上中线长是1，则的最小值是 .‎ 三、解答题：（共70分）‎ ‎17．（共12分）已知数列满足是等差数列，且.‎ ‎（1）求数列和的通项公式；‎ ‎（2）若,求数列的前项和.‎ ‎18．（共12分）2015年12月10日, 我国科学家屠呦呦教授由于在发现青蒿素和治疗疟疾的疗法上的贡献获得诺贝尔医学奖，以青蒿素类药物为主的联合疗法已经成为世界卫生组织推荐的抗疟疾标准疗法，目前，国内青蒿人工种植发展迅速，调查表明，人工种植的青蒿的长势与海拔高度、土壤酸碱度、空气湿度的指标有极强的相关性，现将这三项的指标分别记为，并对它们进行量化：表示不合格，表示临界合格，表示合格，再用综合指标的值评定人工种植的青蒿的长势等级：若，则长势为一级；若，则长势为二级；若，则长势为三级；为了了解目前人工种植的青蒿的长势情况，研究人员随机抽取了块青蒿人工种植地，得到如下结果：‎ 种植地编号 种植地编号 ‎（1）在这10块青蒿人工种植地中任取两地，求这两地的空气湿度的指标相同的概率；‎ ‎（2）从长势等级是一级的人工种植地中任取一地，其综合指标为 ‎，从长势等级不是一级的人工种植地中任取一地，其综合指标为，记随机变量，求的分布列及其数学期望.‎ ‎19．（共12分）如图，已知长方形中，，为的中点，将沿折起，使得平面平面．‎ ‎（1）求证：；‎ ‎（2）若点是线段上的一动点，问点在何位置时，二面角的余弦值为．‎ ‎20.（共12分）如图，在平面直角坐标系中，已知圆，椭圆，为椭圆右顶点．过原点且异于坐标轴的直线与椭圆交于两点，直线与圆的另一交点为，直线与圆的另一交点为，其中．设直线的斜率分别为．‎ ‎（1）求的值；‎ ‎（2）记直线的斜率分别为，是否存在常数，使 得？若存在，求值；若不存在，说明理由.‎ ‎21．（共12分）已知函数，其中常数．‎ ‎（1）当，求函数的单调递增区间；‎ ‎（2）设定义在上的函数在点处的切线方程为，若在内恒成立，则称为函数的“类对称点”，当时，试问是否存在“类对称点”，若存在，请至少求出一个“类对称点”的横坐标；若不存在，请说明理由．‎ 请考生在题（22）（23）中任选一题作答，如果多做，则按所做的的第一题计分．做题时用2B铅笔在答题卡上把所选题目对应的题号涂黑．‎ ‎22.（共10分）已知曲线的极坐标方程为，曲线的参数方程是，射线与曲线交于极点外的三点.‎ ‎（1）求的值；‎ ‎（2）当时，两点在曲线上，求与的值.‎ ‎23．（共10分）已知都是正数.‎ ‎（1）若，求证：；‎ ‎（2）求证：.‎ 高三理科数学答案 ‎1-12 DCABA ABBCB BD 13. 14. 15. 16. ‎ ‎17.（1）由可得，两式作差可得，又适合此通项公式，所以；由此可得由等差数列的性质可得；（2）由题意写出数列的通项公式，再用分组求和法求之即可.‎ 试题解析： （1） ,两式相减可得 ,‎ 当时，，所以是以为首项，为公比的等差数列，所以，.‎ ‎（2），‎ ‎18.（1）由表可知：空气温度指标为的有；空气温度指标为的有,空气温度指标为的有.所以空气温度指标相同的概率.‎ ‎（2）计算块青蒿人工种植地的综合指标, 可得下表：‎ 编号 综合指标 其中长势等级是一级的有，共个，长势等级不是一级的有，共个.随机变量的所有可能取值为：.,‎ ‎,,所以的分布列为：‎ 所以.‎ ‎19.（1）因为平面平面，，为的中点，‎ ‎，取的中点，连结，则平面，取的中点，‎ 连结，则，以为原点如图建立空间直角坐标系，根据已知条件，得 ‎，则，，所以，故．‎ ‎（2）设，因为平面的一个法向量，，．‎ 设平面的一个法向量为，，‎ 取，得，所以，因为，求得 ‎ ‎20.（1）设，则，‎ 所以 ‎ ‎（2）联立得，‎ 解得，联立得，‎ 解得， 所以，，‎ 所以，故存在常数，使得． ‎ ‎ ‎ ‎ ‎ ‎21.（1）函数的定义域为，∵，∴，∵，∴，令，即，∵，∴或，所以函数的单调递增区间是；‎ ‎（2）当时，，∴，‎ ‎，‎ 令，‎ 则，，当时，在上单调递减．∴当时，，从而有时，，当时，在上单调递减，∴当时，，从而有时，，‎ ‎∴当时，不存在“类对称点”．当时，，‎ ‎∴在上是增函数，故，所以当时，存在“类对称点”．‎