人教版高三数学总复习课时作业23 10页

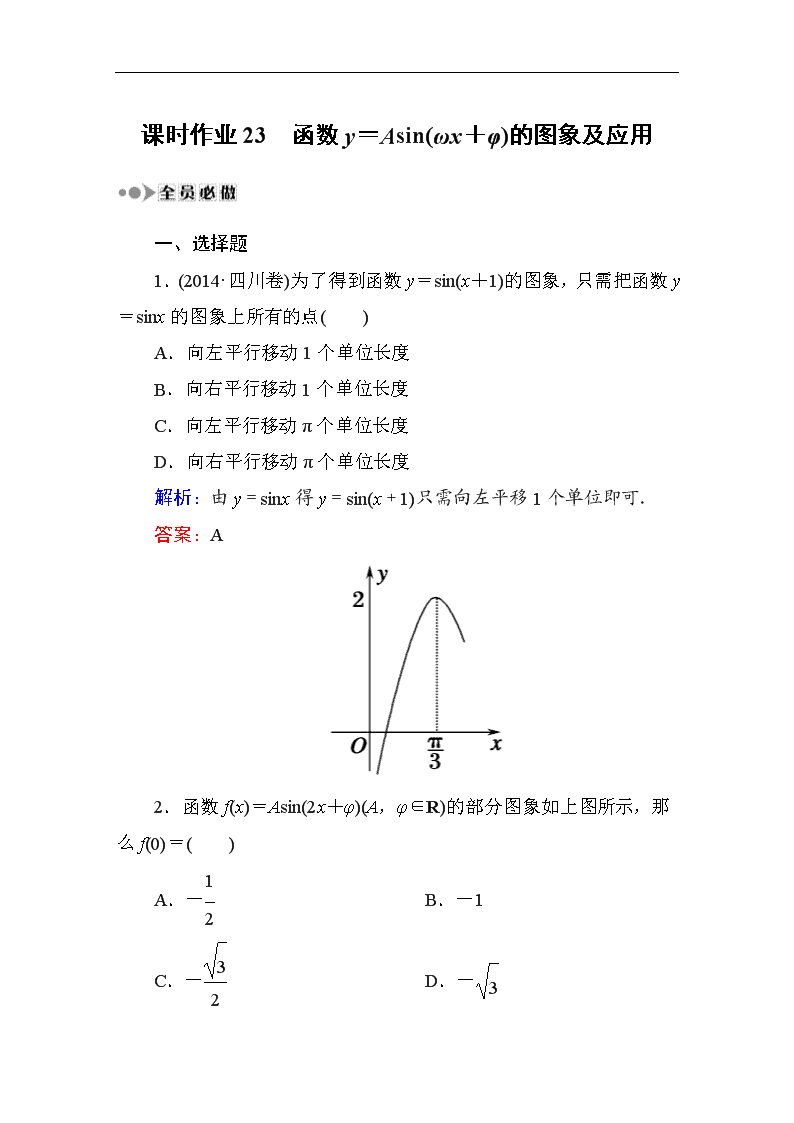
课时作业23　函数y＝Asin(ωx＋φ)的图象及应用 一、选择题 ‎1．(2014·四川卷)为了得到函数y＝sin(x＋1)的图象，只需把函数y＝sinx的图象上所有的点(　　)‎ A．向左平行移动1个单位长度 B．向右平行移动1个单位长度 C．向左平行移动π个单位长度 D．向右平行移动π个单位长度 解析：由y＝sinx得y＝sin(x＋1)只需向左平移1个单位即可．‎ 答案：A ‎2．函数f(x)＝Asin(2x＋φ)(A，φ∈R)的部分图象如上图所示，那么f(0)＝(　　)‎ A．－ B．－1‎ C．－ D．－ 解析：由图象知A＝2，图象过点(，2)，‎ ‎∴2sin(×2＋φ)＝2，‎ ‎∴＋φ＝＋2kπ，k∈Z，‎ ‎∴φ＝－＋2kπ，k∈Z，‎ ‎∴φ＝－，∴f(0)＝2sin(－)＝－1.‎ 答案：B ‎3．(2014·安徽卷)若将函数f(x)＝sin2x＋cos2x的图象向右平移φ个单位，所得图象关于y轴对称，则φ的最小正值是(　　)‎ A. B. C. D. 解析：f(x)＝sin2x＋cos2x＝sin(2x＋)，向右平移φ个单位，得y＝sin(2x－2φ＋)关于y轴对称，则－2φ＋＝＋kπ，k∈Z，φ＝－－，k∈Z，φ的最小正值为π.‎ 答案：C ‎4．(2014·辽宁卷)将函数y＝3sin(2x＋)的图象向右平移个单位长度，所得图象对应的函数(　　)‎ A．在区间[，]上单调递减 B．在区间[，]上单调递增 C．在区间[－，]上单调递减 D．在区间[－，]上单调递增 解析：平移后的函数为y＝3sin[2(x－)＋]＝3sin(2x＋－π)＝3sin(2x－π)，增区间：－＋2kπ≤2x－π≤＋2kπ，k∈Z，即＋kπ≤x≤π＋kπ，k∈Z，k＝0时，≤x≤π，故选B.‎ 答案：B ‎5．函数f(x)＝Asin(ωx＋φ)(A>0，ω>0)的图象如图所示，则f(1)＋f(2)＋f(3)＋…＋f(2 015)＝(　　)‎ A．0 B. C.＋1 D．1‎ 解析：由图象知φ＝0，ω＝＝，∴f(x)＝2sin，其图象关于(4,0)，x＝2，x＝6对称，∴f(1)＋f(2)＋f(3)＋…＋f(8)＝0，∵T＝8,2 015＝251×8＋7，∴f(1)＋f(2)＋f(3)＋…＋f(2 015)＝f(0)＋f(1)＋…＋f(2 015)－f(0)＝－f(0)＝0.‎ 答案：A ‎6．函数f(x)＝sin(ωx＋φ)的最小正周期是π，若其图象向右平移个单位后得到的函数为奇函数，则函数f(x)的图象(　　)‎ A．关于点对称 B．关于直线x＝对称 C．关于点对称 D．关于直线x＝对称 解析：∵＝π，∴ω＝2.∴f(x)＝sin(2x＋φ)向右平移个单位，得y＝sin为奇函数，‎ ‎∴－＋φ＝kπ(k∈Z)，∴φ＝＋kπ(k∈Z)，‎ ‎∴φ＝，∴f(x)＝sin.‎ ‎∵sin＝1，‎ ‎∴直线x＝为函数的对称轴．故选B.‎ 答案：B 二、填空题 ‎7．函数y＝Asin(ωx＋φ)(A，ω，φ为常数，A>0，ω>0)在闭区间[－π，0]上的图象如图所示，则ω＝________.‎ 解析：由图象可以看出T＝π，‎ ‎∴T＝π＝，因此ω＝3.‎ 答案：3‎ ‎8．某城市一年中12个月的平均气温与月份的关系可近似地用三角函数y＝a＋Acos(x＝1,2,3，…，12，A>0)来表示，已知6月份的月平均气温最高，为‎28℃‎，12月份的月平均气温最低，为‎18℃‎，则10月份的平均气温值为________℃.‎ 解析：由题意得∴ ‎∴y＝23＋5cos，‎ x＝10时，y＝23＋5×＝20.5.‎ 答案：20.5‎ ‎9．若将函数y＝tan(ω>0)的图象向右平移个单位长度后，与函数y＝tan的图象重合，则ω的最小值为________．‎ 解析：y＝tan向右平移个单位长度后得到函数解析式为y＝tan[ω(x－)＋]＝tan，显然当－＝＋kπ，k∈Z时，两图象重合，此时ω＝－6k，k∈Z.∵ω>0，∴k＝0时，ω的最小值为.‎ 答案： 三、解答题 ‎10．已知函数f(x)＝sin＋1.‎ ‎(1)求它的振幅、最小正周期、初相；‎ ‎(2)画出函数y＝f(x)在上的图象．‎ 解：(1)振幅为，最小正周期T＝π，初相为－.‎ ‎(2)图象如图所示．‎ ‎11．设函数f(x)＝(sinωx＋cosωx)2＋2cos2ωx(ω>0)的最小正周期为.‎ ‎(1)求ω的值；‎ ‎(2)若函数y＝g(x)的图象是由y＝f(x)的图象向右平移个单位长度得到．求y＝g(x)的单调增区间．‎ 解：(1)f(x)＝sin2ωx＋cos2ωx＋2sinωxcosωx＋1＋cos2ωx＝sin2ωx＋cos2ωx＋2＝sin＋2，‎ 依题意得＝，故ω＝.‎ ‎(2)依题意得 g(x)＝sin＋2＝sin＋2.‎ 由2kπ－≤3x－≤2kπ＋(k∈Z)解得 kπ＋≤x≤kπ＋(k∈Z)．‎ 故g(x)的单调增区间为(k∈Z)．‎ ‎1．电流强度I(安)随时间t(秒)变化的函数I＝Asin(ωt＋φ)(A>0，ω>0,0<φ<)的图象如上图所示，则当t＝秒时，电流强度是(　　)‎ A．－5安 B．5安 C．5安 D．10安 解析：由图象知A＝10，＝－＝，‎ ‎∴ω＝＝100π.∴I＝10sin(100πt＋φ)．‎ 为五点中的第二个点，‎ ‎∴100π×＋φ＝.‎ ‎∴φ＝.∴I＝10sin，‎ 当t＝秒时，I＝－5安．‎ 答案：A ‎2．(2014·江苏卷)已知函数y＝cosx与y＝sin(2x＋φ)(0≤φ ‎<π)，它们的图象有一个横坐标为的交点，则φ的值是________．‎ 解析：由题意cos＝sin，‎ 即sin＝，＋φ＝kπ＋(－1)k·(k∈Z)．‎ 因为0≤φ<π，所以φ＝.‎ 答案： ‎3．已知函数f(x)＝sin(ωx＋φ)的图象上的两个相邻的最高点和最低点的距离为2，且过点，则函数解析式f(x)＝________.‎ 解析：据已知两个相邻最高和最低点距离为2，可得＝2，解得T＝4，故ω＝＝，即f(x)＝sin，又函数图象过点，故f(2)＝sin＝－sinφ＝－，又－≤φ≤，解得φ＝，故f(x)＝sin.‎ 答案：sin ‎4．已知函数f(x)＝Asin(ωx＋φ)(x∈R，A>0，ω>0,0<φ<)的部分图象如图所示，P是图象的最高点，Q为图象与x轴的交点，O为坐标原点．若OQ＝4，OP＝，PQ＝.‎ ‎(1)求函数y＝f(x)的解析式；‎ ‎(2)将函数y＝f(x)的图象向右平移2个单位后得到函数y＝g(x)的图象，当x∈[0,3]时，求函数h(x)＝f(x)·g(x)的值域．‎ 解：(1)由条件，cos∠POQ＝＝，所以P(1,2)．‎ 因为A＝2，周期T＝4×(4－1)＝12，‎ 又＝12，则ω＝.‎ 将点P(1,2)代入f(x)＝2sin(x＋φ)，得sin(＋φ)＝1，因为0<φ<，所以φ＝，所以f(x)＝2sin(x＋)．‎ ‎(2)由题意，可得g(x)＝2sinx.‎ 所以h(x)＝f(x)·g(x)＝4sin(x＋)·sinx＝2sin2x＋2sinx·cosx＝1－cosx＋sinx＝1＋2sin(x－)．‎ 当x∈[0,3]时，x－∈[－，]，所以sin(x－)∈[－，1]，‎ 所以函数h(x)的值域为[0,3]．‎