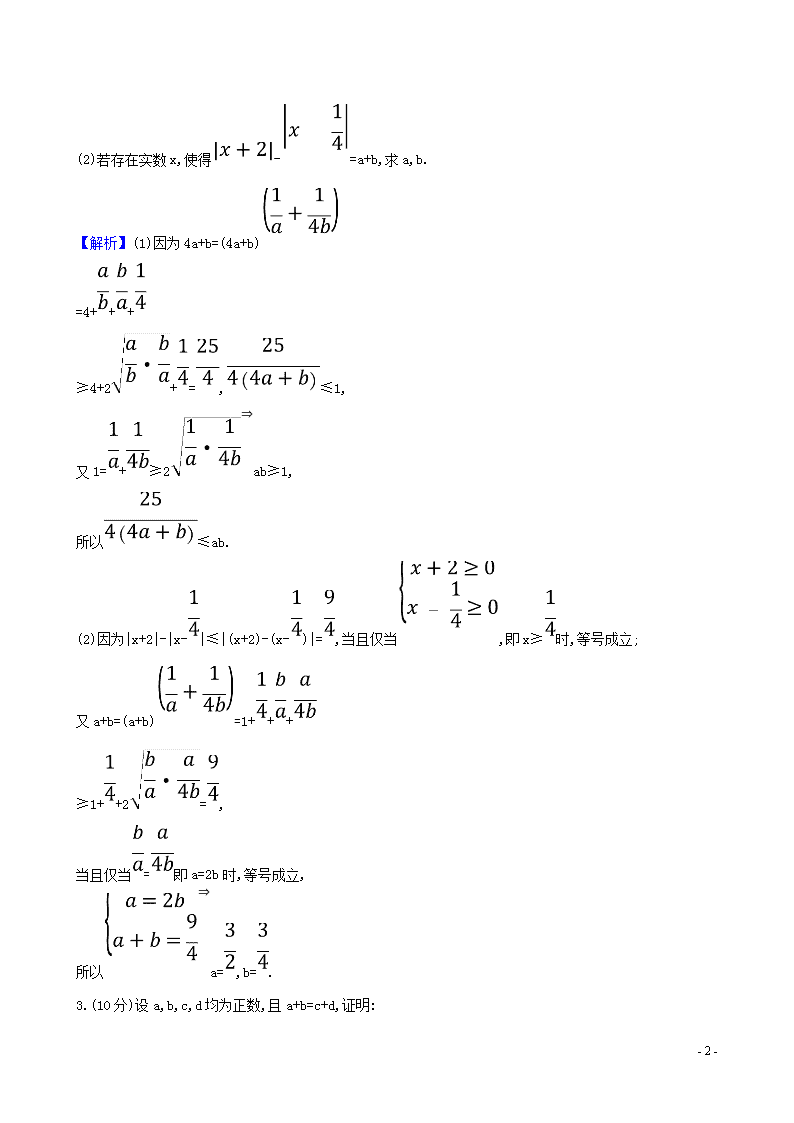2021版高考数学一轮复习核心素养测评八十证明不等式的基本方法理北师大版 4页

核心素养测评八十 证明不等式的基本方法 ‎1.(10分)已知a,b都是正实数,且a+b=2,求证:+≥1.‎ ‎【证明】因为a>0,b>0,a+b=2,‎ 所以+-1‎ ‎=‎ ‎=‎ ‎=‎ ‎==‎ ‎=.‎ 因为a+b=2≥2,所以ab≤1.‎ 所以≥0.所以+≥1.‎ ‎2.(10分)(2020·桂林模拟)已知正数a,b满足+=1.‎ ‎(1)证明:≤ab.‎ - 4 -‎ ‎(2)若存在实数x,使得-=a+b,求a,b.‎ ‎【解析】(1)因为4a+b=(4a+b)‎ ‎=4+++‎ ‎≥4+2+=,≤1,‎ 又1=+≥2⇒ab≥1,‎ 所以≤ab.‎ ‎(2)因为|x+2|-|x-|≤|(x+2)-(x-)|=,当且仅当,即x≥时,等号成立;‎ 又a+b=(a+b)=1+++‎ ‎≥1++2=,‎ 当且仅当=即a=2b时,等号成立,‎ 所以⇒a=,b=.‎ ‎3.(10分)设a,b,c,d均为正数,且a+b=c+d,证明:‎ - 4 -‎ ‎(1)若ab>cd,则+>+.‎ ‎(2)+>+是|a-b|<|c-d|的充要条件.‎ ‎【证明】(1)因为a,b,c,d为正数,且a+b=c+d,‎ 欲证+>+,只需证明(+)2>(+)2,也就是证明a+b+2>c+d+2,只需证明>,即证ab>cd.‎ 由于ab>cd成立,因此+>+.‎ ‎(2)①若|a-b|<|c-d|,则(a-b)2<(c-d)2,‎ 即(a+b)2-4ab<(c+d)2-4cd.‎ 因为a+b=c+d,所以ab>cd.‎ 由(1)得+>+.‎ ‎②若+>+,则(+)2>(+)2,‎ 所以a+b+2>c+d+2.‎ 因为a+b=c+d,所以ab>cd.‎ 于是(a-b)2=(a+b)2-4ab<(c+d)2-4cd ‎=(c-d)2.因此|a-b|<|c-d|.‎ 综上,+>+是|a-b|<|c-d|的充要条件.‎ ‎4.(10分)设函数f(x)=|x-2|+2x-3,记f(x)≤-1的解集为M. ‎ ‎(1)求M.‎ ‎(2)当x∈M时,求证:x[f(x)]2-x2f(x)≤0.‎ ‎【解析】(1)由已知,得f(x)=‎ 当x≤2时,由f(x)=x-1≤-1,‎ 解得x≤0,此时x≤0;‎ 当x>2时,由f(x)=3x-5≤-1,‎ 解得x≤,显然不成立.‎ 故f(x)≤-1的解集为M={x|x≤0}.‎ - 4 -‎ ‎(2)当x∈M时,f(x)=x-1,‎ 于是x[f(x)]2-x2f(x)=x(x-1)2-x2(x-1)‎ ‎=-x2+x=-+.‎ 令g(x)=-+,‎ 则函数g(x)在(-∞,0]上是增函数,‎ 所以g(x)≤g(0)=0.‎ 故x[f(x)]2-x2f(x)≤0.‎ - 4 -‎