专题5-4 热点题型三 三角函数的图象与性质-《奇招制胜》2017年高考数学（理）热点+题型全突破 10页

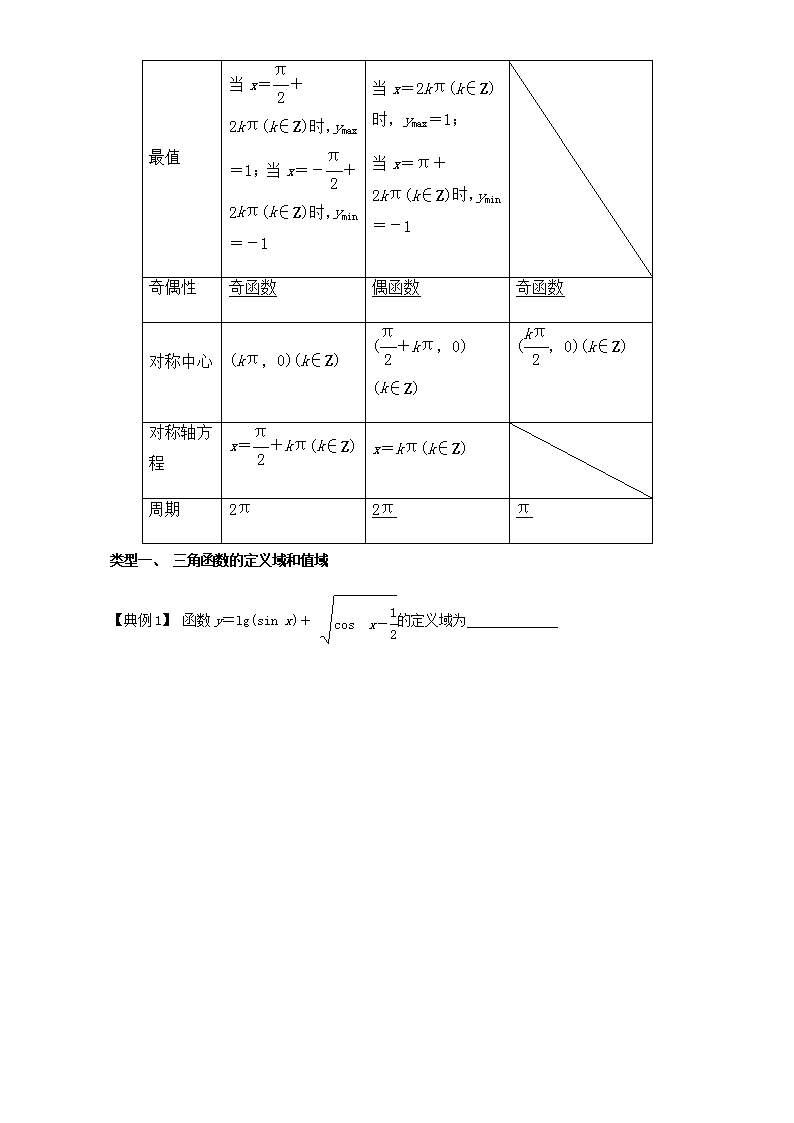
热点题型三 三角函数的图象与性质 ‎【基础知识整合】‎ ‎1．用五点法作正弦函数和余弦函数的简图 正弦函数y＝sin x，x∈0,2π]的图象中，五个关键点是：(0,0)，(，1)，(π，0)，(，－1)，(2π，0)．‎ 余弦函数y＝cos x，x∈0,2π]的图象中，五个关键点是：(0,1)，(，0)，(π，－1)，(，0)，(2π，1)．‎ ‎2．正弦函数、余弦函数、正切函数的图象与性质 函数 y＝sin x y＝cos x y＝tan x 图象 定义域 R R ‎{x|x∈R且x≠＋kπ，k∈Z}‎ 值域 ‎－1,1]‎ ‎－1,1]‎ R 单调性 在－＋2kπ，＋2kπ](k∈Z)上递增；‎ 在＋2kπ，＋2kπ](k∈Z)上递减 在2kπ，π＋2kπ](k∈Z)上递减 在－π＋2kπ，2kπ](k∈Z)上递增；‎ 在(－＋kπ，＋kπ)(k∈Z)上递增 最值 当x＝＋2‎ 当x＝2kπ(k∈Z kπ(k∈Z)时，ymax＝1；当x＝－＋2kπ(k∈Z)时，ymin＝－1‎ ‎)时，ymax＝1；‎ 当x＝π＋2kπ(k∈Z)时，ymin＝－1‎ 奇偶性 奇函数 偶函数 奇函数 对称中心 ‎(kπ，0)(k∈Z)‎ ‎(＋kπ，0) (k∈Z)‎ ‎(，0)(k∈Z)‎ 对称轴方程 x＝＋kπ(k∈Z)‎ x＝kπ(k∈Z)‎ 周期 ‎2π ‎2π π 类型一、 三角函数的定义域和值域 ‎【典例1】 函数y＝lg(sin x)＋ 的定义域为 ‎ ‎【典例2】 【2015·天津模拟】函数f(x)=-sin(2x-),x∈【0, 】的最大值是　　　　.‎ ‎【答案】 ‎ ‎【解析】因为x∈【0, 】,‎ 所以-≤2x-≤.‎ 根据正弦曲线,得当2x-=-时.sin(2x-)取得最小值为-.‎ 故f (x)=-sin(2x-)的最大值为.‎ ‎【变式训练】函数y＝cos2x＋sin x(|x|≤)的最小值为 ．‎ ‎【解析】令t＝sin x，∵|x|≤，‎ ‎∴t∈.‎ ‎∴y＝－t2＋t＋1＝－2＋，‎ ‎∴t＝－时，ymin＝.‎ ‎【解题技巧与方法总结】‎ ‎(1)三角函数定义域的求法 求三角函数定义域实际上是构造简单的三角不等式(组)，常借助三角函数线或三角函数图象来求解．‎ ‎(2)三角函数值域的不同求法 ‎①利用sin x和cos x的值域直接求；‎ ‎②把所给的三角函数式变换成y＝Asin(ωx＋φ)的形式求值域；‎ ‎③通过换元，转换成二次函数求值域．‎ 类型二 三角函数的单调性 ‎【典例3】 【2015高考安徽，理10】已知函数（，，均为正的常数）的最小正周期为，当时，函数取得最小值，则下列结论正确的是（ ）‎ ‎ （A） （B）‎ ‎ （C） （D）‎ ‎【答案】A ‎【考点定位】1.三角函数的图象与应用；2.函数值的大小比较.‎ ‎【思路点拨】对于三角函数中比较大小的问题，一般的步骤是：第一步，根据题中所给的条件写出三角函数解析式，如本题通过周期判断出，通过最值判断出，从而得出三角函数解析式；第二步，需要比较大小的函数值代入解析式或者通过函数图象进行判断，本题中代入函数值计算不太方便，故可以根据函数图象的特征进行判断即可.‎ ‎【典例4】 【2015高考新课标1】 函数的部分图像如图所示，则的单调递减区间为 ‎ ‎【答案】‎ ‎【解析】由五点作图知，，解得，，所以，令，解得＜＜，，故单调减区间为（，），.‎ ‎【变式训练】‎ ‎【2016济南模拟】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象与直线y=b(00)的形式．‎ ‎2．对于函数的性质(定义域、值域、单调性、对称性、最值等)可以通过换元的方法令t＝ωx＋φ，将其转化为研究y＝sin t的性质．‎ ‎3．对于已知函数的单调区间的某一部分确定参数ω的范围的问题：首先，明确已知的单调区间应为函数的单调区间的子集；其次，要确定已知函数的单调区间，从而利用它们之间的关系可求解．‎ ‎【失误与防范】‎ ‎1．闭区间上最值或值域问题，首先要在定义域基础上分析单调性，含参数的最值问题，要讨论参数对最值的影响．‎ ‎2．要注意求函数y＝Asin(ωx＋φ)的单调区间时ω的符号，若ω<0，那么一定先借助诱导公式将ω化为正数．‎ ‎3．三角函数的最值可能不在自变量区间的端点处取得，直接将两个端点处的函数值作为最值是错误的．‎