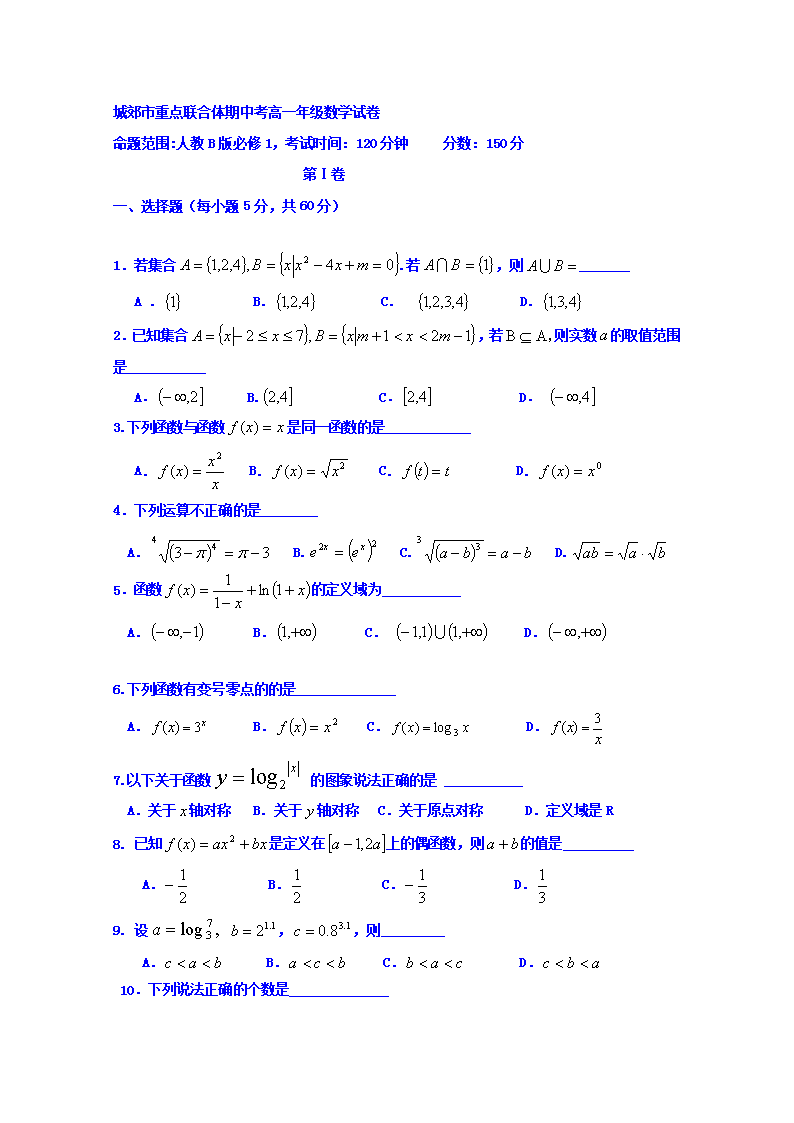辽宁省沈阳市城郊市重点联合体2019-2020学年高一上学期期中考试（2）数学试卷 7页

www.ks5u.com 城郊市重点联合体期中考高一年级数学试卷 命题范围:人教B版必修1，考试时间：120分钟 分数：150分 第Ⅰ卷 一、选择题（每小题5分，共60分）‎ ‎1．若集合.若，则_______ ‎ A ． B． C． D．‎ ‎2．已知集合，若则实数的取值范围是___________‎ A． B. C． D． ‎ ‎3.下列函数与函数是同一函数的是____________‎ A． B． C． D．‎ ‎4．下列运算不正确的是________‎ A． B. C. D.‎ ‎5．函数的定义域为___________‎ A． B． C． D．‎ ‎ ‎ ‎6.下列函数有变号零点的的是______________‎ A． B． C． D．‎ ‎7.以下关于函数 的图象说法正确的是 ___________ ‎ A．关于轴对称 B．关于轴对称 C．关于原点对称 D．定义域是R ‎8. 已知是定义在上的偶函数，则的值是__________ ‎ A． B． C． D．‎ ‎9. 设 ，，则_________ ‎ A． B． C． D．‎ ‎ 10．下列说法正确的个数是______________‎ ‎（1）函数在定义域上是减函数；‎ ‎（2）奇函数必过原点；‎ ‎ （3）幂函数的图象都不经过第四象限；‎ ‎（4）函数的图象与函数的图象关于直线对称 A．1 B．2 C．3 D．4‎ ‎11．已知函数的单调增区间为__________ ‎ ‎ A． B． C． D． ‎ ‎12. 已知函数= 在R上为减函数，则实数的取值范围为______ ‎ A． B． C． D． ‎ 第Ⅱ卷 二、填空题（共4小题，每小题5分，共20分.请把答案填在答题卡相应位置.）‎ ‎13.当且时，函数的图象必过定点_____________．‎ ‎14.若函数的定义域为，则函数的定义域为____________.‎ ‎15．已知是奇函数，当时，，则当时，=__________‎ ‎16.函数对任意实数都满足，且方程有3个实数根，则这3个实数根的和为_______________.‎ 三、解答题（共6小题，共70分.解答应写出文字说明、推证过程或演算步骤.）‎ ‎17.（本小题10分）已知函数 的定义域为集合A，函数的值域为集合B.‎ ‎（1）求集合A,B;‎ ‎（2）求集合.‎ ‎18.（本小题12分） 已知函数 ‎ ‎ （1）求的值；‎ ‎（2）求的值；‎ ‎（3）当时，求函数的值域.‎ ‎19．（本小题12分）已知函数 ‎ ‎（1）若，求函数的值域；‎ ‎（2）设函数，若在区间上是单调函数，求实数的取值范围.‎ ‎ ‎ ‎20．（本小题12分）已知一次函数，且在上递增，二次函数的图象的顶点是且过.‎ ‎(1)分别求函数与函数的解析式；‎ ‎(2)求函数与的解析式．‎ ‎21. （本小题12分）已知函数 ‎（1）令，求关于的函数关系式；‎ ‎（2）求函数的最大值和最小值.‎ ‎22．（本小题12分）已知函数是定义在上的减函数，且 ‎ （1）求的值；‎ ‎（2）若成立，求的取值范围；‎ 城郊市重点联合体期中考试高一年级数学参考答案及评分标准 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 C D C D C C B D A B D B ‎13.(2017,-2017) 14.［0,1 ］‎ ‎15. 16． ‎ ‎17. 解：(1) A= ………………………………2分 B=(2,8) …………………………4分 ‎ (2) ……………………………6分 ‎ ………………………………8分 ‎ …………………10分 ‎ ‎18.（1）………………………………2分 ‎ …………………………4分 ‎（2）………………………………8分 ‎（3）‎ ‎ X=0时，f(x)=0 …………………10分 终上所述:f(x)的值域为 …………………12分 ‎19. 解：（1）解：对称轴为 x=，开口向上对称轴处取最小值………2分 由图像得， 时函数递减，时函数递增 ‎ ， ， f(x)的最大值为2 ………………4分 f(x)的值域为 ………………6分 ‎（2）g（x）= ‎ 对称轴为 x= …………………8分 因为在区间上是单调函数 所以……………………10分 解得： …………………12分 ‎20．解：‎ ‎（1）因为在上递增 ∴设f（x）=kx+b （k>0）‎ ‎∴, ………………………………2分 ‎ ‎ 解得 k=2 k=-2‎ ‎ b=1 或 b=-3（舍去）‎ ‎∴f（x）=2x+1 …………………………4分 ‎ ‎∵函数g（x）的顶点是（1，-2）‎ ‎∴设g（x）= …………………………6分 g（x）过点（0，-1），代入解得a=1‎ ‎∴g（x）=x2 -2x﹣1 …………………………8分 ‎（2） …………………………10分 ‎ …………………………12分 ‎21、解（1） ………………3分 令，所以y= ……………………6分 ‎（2） ………………… ………8分 对称轴为 t=,二次函数开口向上对称轴处取最小值为…… 10分 由图像得， 时函数递减，时函数递增 当t=1时，y=0;‎ 当t=3时，y=1‎ 综上所述， …………………………… 12分 ‎ ‎22. 解：（1）令x=y=1, 解得f（1）=0……3分 ‎（2） ……………………5分 ‎ ……………………7分 ‎ 函数是定义在上的减函数，所以 ‎ ……………………10分 ‎ ‎ 解得……………………12分