数学文卷·2019届山东省淄博市淄川中学高二上学期第一次月考（2017-09） 8页

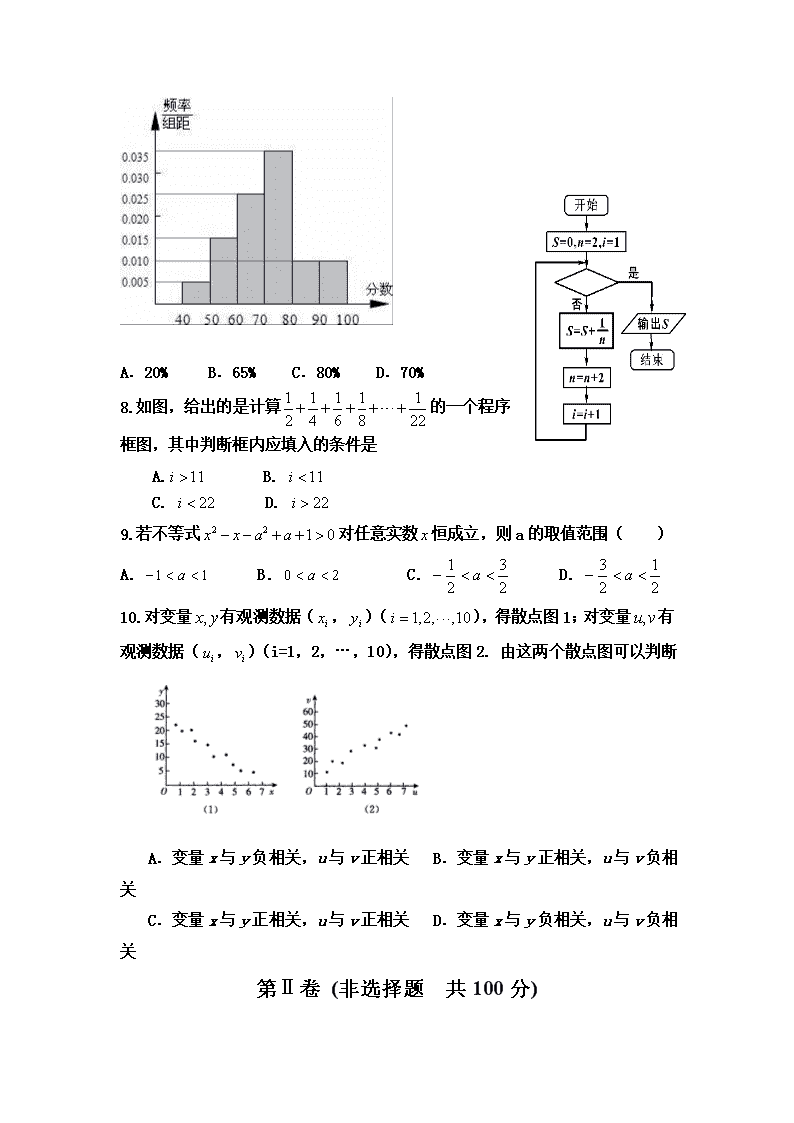
高2016级文科数学第一次阶段检测 一、选择题（每小题5分，共50分，请将正确选项填涂在答题卡上）.‎ ‎1．如果a＜b＜0，那么( )．‎ A． B．ac＜bc C．＞ D．a2＜-0b2‎ ‎2.不等式 的解集是为( )‎ ‎（A） （B）（-2，1） （C） （D）∪‎ ‎3．已知各项均为正数的等比数列{an}，a1•a9=16，则a2•a5•a8的值（　　）‎ A．16 B．32 C．48 D．64‎ ‎4．在△ABC中，若AB=，BC=3，∠C=120°，则AC=（　　）‎ A．4 B．2 C．3 D．1‎ ‎5．若x，y满足，则x﹣y的最小值为（　　）‎ A．﹣3 B．﹣1 C．﹣4 D．-2‎ ‎6.某商场连续10天对甲商品每天的销售量（单位：件）进行了统计，得到如图所示的茎叶图，据该图估计商店一天的销售量不低于40件的频率为（　　）‎ A． B． C． D．‎ ‎7．统计某校1000名学生的数学水平测试成绩，得到样本频率分布直方图如图所示，若满分为100分，规定不低于60分为及格，则及格率是（　　）‎ A．20% B．65% C．80% D．70%‎ ‎8.如图，给出的是计算的一个程序 框图，其中判断框内应填入的条件是 ‎ A. B. ‎ C. D. ‎ ‎9.若不等式对任意实数恒成立，则a的取值范围（ ） ‎ A． ‎ B． C． D． ‎ ‎10.对变量有观测数据（，）（），得散点图1；对变量有观测数据（，）（i=1，2，…，10），得散点图2. 由这两个散点图可以判断 ‎ ‎ A．变量x与y负相关，u与v正相关 B．变量x与y正相关，u与v负相关 C．变量x与y正相关，u与v正相关 D．变量x与y负相关，u与v负相关 第Ⅱ卷 (非选择题 共100分)‎ 二、填空题：（本大题共5小题，每小题5分，共25分） 11.若直线y=3x上存在点（x，y）满足约束条件则实数m的最大值为　　‎ ‎12．已知正数x、y满足+=1，则x+y的最小值是　　．‎ ‎13．执行如右图所示的程序框图，输出的值为 . ‎ ‎14.不等式的解集是 ‎ ‎15.从一堆产品（其中正品与次品都多于2件）中任取2件，‎ 观察正品件数和次品件数．则下列说法：①恰好有1件次 品和恰好有2件次品是互斥事件；②至少有1件次品和全 是次品是对立事件；③至少有1件正品和至少有1件次品是互斥事件但不是对立事件；④至少有1件次品和全是正品是互斥事件也是对立事件．其中正确的有______（写出所有正确说法的序号）．‎ 三、解答题:（本大题共6小题，共75分。写出文字说明，证明过程或演算步骤。）‎ ‎16. (本小题满分12分)甲、乙两个人进行“剪子、包袱、锤”的游戏，两人都随机出拳，求一次游戏甲不输的概率。‎ ‎17.(本小题满分12分)‎ 若不等式x2﹣ax+b＜0的解集为（1，3），求不等式＜的解集。‎ ‎18.(本小题满分12分)‎ 为了解下属某部门对本企业职工的服务情况，随机访问部分职工，根据被访问职工对该部门的评分，绘制频率分布直方图（如图所示).‎ ‎50 60 70 80 90 100 评分 频率 ‎ 组距 ‎ ‎0.010‎ ‎0.015‎ ‎0.005‎ ‎0.020‎ ‎0.025‎ ‎0.030‎ ‎0.035‎ ‎0‎ ‎0.040‎ ‎（Ⅰ）为进一步了解情况，该企业决定在 第组中用分层抽样抽取名职工进 行座谈，求第组中各自抽取的人数 ‎（Ⅱ）求该样本平均数和中位数 ‎ 19．(本题满分13分）下表提供了某厂生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据：‎ x ‎2‎ ‎4‎ ‎6‎ ‎8‎ ‎10‎ y ‎5‎ ‎6‎ ‎5‎ ‎9‎ ‎10‎ (1) 请根据上表提供的数据，用最小二乘法求出关于的线性回归方程 ‎(参考公式： )‎ ‎(2)根据(1)求出的线性回归方程，预测生产20吨甲产品的生产能耗是多少吨标准煤？‎ ‎20.(本题满分13分）已知函数f(x)＝x2－ax (a∈R)．‎ ‎（1）若a=2,求不等式f(x)≥3的解集 ‎（2）若x∈[1，＋∞)时，f(x)≥－x2－2恒成立，求a的取值范围 ‎21.（本题满分13分）‎ 已知数列是等差数列，数列是等比数列，且 ‎（Ⅰ）求和的通项公式；‎ ‎（Ⅱ）设，求数列的前项和．‎ 高2016级文科数学第一次阶段检测答案 一、选择题（共10小题，每小题5分，共50分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 C B D D A B C A C A 二．填空题（共5小题，每小题5分，共25分）‎ ‎11. 12．．13．19 14. 15.①④‎ 三、解答题:（本大题共6小题，共75分。写出文字说明，证明过程或演算步骤.）‎ ‎16.解：方法一：所有可能的基本事件为：(剪子，剪子)，(剪子，包袱) ，(剪子，锤) ，(包袱，剪子)，(包袱、包袱) ，(包袱，锤) ，(锤，剪子) ，(锤、包袱)，(锤，锤) ，共9个基本事件----------------------4分 记“一次游戏甲不输”为事件A，则事件A包含的基本事件为(剪子，剪子)，(包袱、包袱) ，(锤，锤) ,(包袱，锤) ，(锤，剪子) ，(剪子，包袱) 共6个基本事件---------------------8分 根据古典概型的概率计算公式得--------------------12分 方法二:用对立事件做也行 两种方法都必须列出所有可能的基本事件和事件A，运用古典概型必须先写出原始数据再约分，否则不给分。‎ ‎17.解：因为不等式x2﹣ax+b＜0的解集为（1，3），‎ 所以1+3=a，1×3=b，即a=4，b=3……………………………………6分 所以不等式＜即，‎ 整理得，‎ 解得，‎ 所以不等式的解集为：………………………………12分 ‎18.（本小题满分12分）‎ 解：（Ⅰ)第组的频率之比为3:2:1‎ 则第组抽取的人数为人；第组为人；第组为人.‎ ‎----------------------4分 ‎（Ⅱ）‎ 样本平均数 ‎ ----------8分 设中位数为x ‎0.05+0.35+0.03（x-70）=0.5‎ ‎------------------12分 ‎19．(1)由题意：‎ ‎＝＝6-------------1分 ‎＝＝7------------2分 ‎=-------------4分 ‎＝------------6分 则＝＝0.65------------8分 ‎＝－＝7－0.65×6＝3.1------------10分 故线性回归方程为.------------11分 ‎(2)根据线性回归方程的预测，现在生产当吨时，产品消耗的标准煤的数量为：‎ ‎-----------13分 ‎20.（1）若a=2,f(x)≥3即x2－2x－ 3≥0‎ ‎（x-3)（x+1）≥0 所以{x|x≤-1或x≥3}……………6分 ‎（2）当x∈[1，＋∞)时，f(x)≥－x2－2恒成立，求a的取值范围．‎ 解：f(x)≥－x2－2即在x∈[1，＋∞)时恒成立，…………………………………………8分 令，等价于在x∈[1，＋∞)时恒成立，…………………………………………10分 所以，当且仅当 所以a≤4.…………………………………………12分 故所求a的取值范围是.…………………………………………13分 ‎ 21.解：（Ⅰ）设等差数列的公差为，设等比数列的公比为 ‎（Ⅱ）由（Ⅰ）知，，-----------------9分 从而数列的前项和 ‎．………………………………13分