2017-2018学年广东省汕头市潮南实验学校高二下学期期中考试数学（文）试题 8页

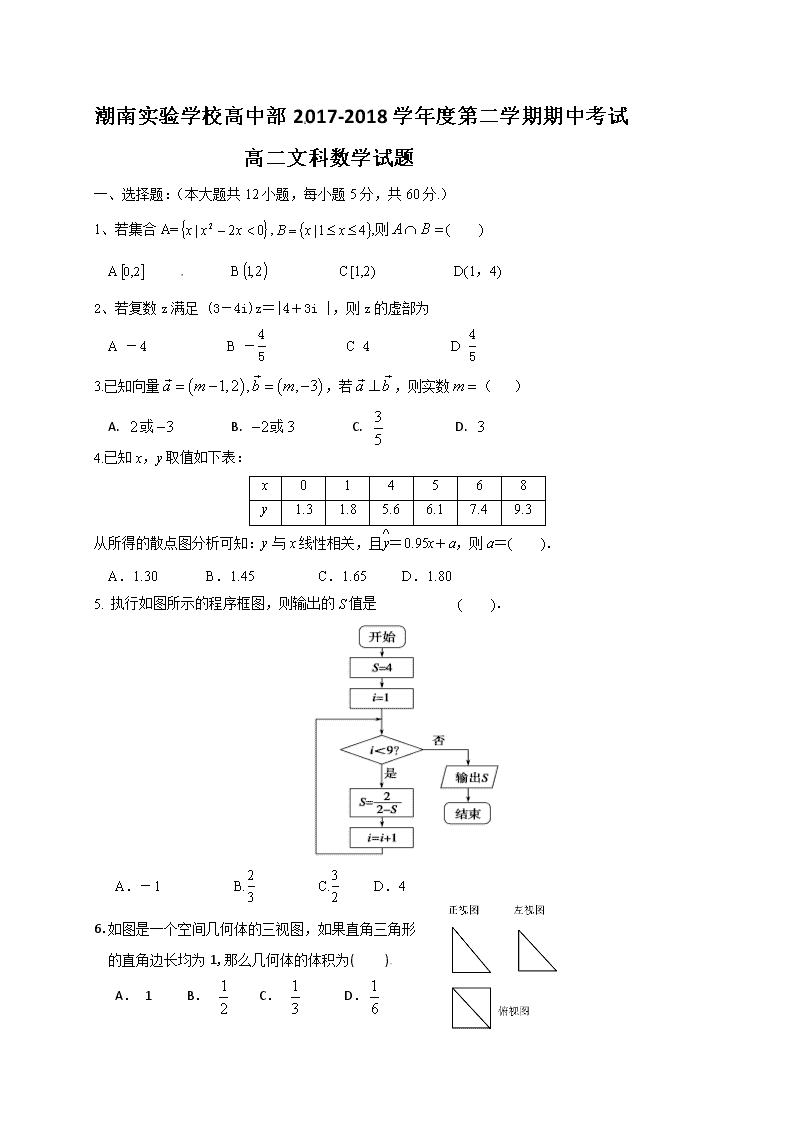
潮南实验学校高中部2017-2018学年度第二学期期中考试 ‎ 高二文科数学试题 一、选择题：（本大题共12小题，每小题5分，共60分.）‎ ‎1、若集合A=,,则( ) ‎ ‎ A B C D(1，4)‎ ‎2、若复数z满足 (3－4i)z＝|4＋3i |，则z的虚部为 A －4 B － C 4 D ‎3.已知向量，若，则实数（ ）‎ A. 或 B. 或 C. D. ‎ ‎4.已知x，y取值如下表：‎ x ‎0‎ ‎1‎ ‎4‎ ‎5‎ ‎6‎ ‎8‎ y ‎1.3‎ ‎1.8‎ ‎5.6‎ ‎6.1‎ ‎7.4‎ ‎9.3‎ 从所得的散点图分析可知：y与x线性相关，且＝0.95x＋a，则a＝(　　)．‎ A．1.30 B．1.45 C．1.65 D．1.80‎ ‎5. 执行如图所示的程序框图，则输出的S值是 (　　)．‎ A．－1 B. C. D．4‎ ‎6.如图是一个空间几何体的三视图，如果直角三角形 的直角边长均为1,那么几何体的体积为(　　 )‎ ‎ A． 1 B． C． D． ‎ ‎7.若函数在上存在零点，则正实数的取值范围是（ ）‎ ‎ A B C D ‎8．函数的图象是( )‎ ‎9.设椭圆C：（a＞b＞0）的左、右焦点分别为F1、F2，P是C上的点PF2⊥F1F2，∠PF1F2=30°，则C的离心率为（　　）‎ A． B． C． D．‎ ‎10.若f（x）=﹣+blnx在（0，2）上是增函数，则b的取值范围是（　　）‎ A．[4，+∞） B．（4，+∞） C．（﹣∞，4] D．（﹣∞，4）‎ ‎11.若直线 与曲线有且只有两个公共点，则的取值范围是（ ）‎ ‎ A B C D ‎12. 已知函数处取得极大值，在处取得极小值，满足的取值范围是（ ）‎ ‎ A. B. C. D. ‎ 二、填空题（每题5分，满分20分，将答案填在答题纸上）‎ ‎13.设向量，且，则=_________.‎ ‎14. 则f（f（2））的值为　　 ．‎ ‎15.已知函数满足，且对一切都成立，当时， ‎ ‎，则_________.‎ ‎16．已知球O的半径为R，A，B，C三点在球O的球面上，球心O到平面ABC的距离为，AB=AC=2，∠BAC=120°，则球O的表面积为　 　．‎ 三、 解答题（本大题共6小题，满分12+12+12+12+12+10=70分）‎ ‎17.（本题满分12分）‎ 设数列{an}满足a1＋3a2＋32a3＋…＋3n－1an＝，n∈N.‎ ‎(1)求数列{an}的通项；‎ ‎(2)设bn＝，求数列{bn}的前n项和Sn.‎ ‎18.（本小题满分12分）有甲、乙两个班级进行数学考试，按照大于等于85分 为优秀，85分以下为非优秀统计成绩后，得到如下的列联表.‎ 优秀 非优秀 总计 甲班 ‎10‎ 乙班 ‎30‎ 合计 ‎105‎ 已知从全部105人中随机抽取1人为优秀的概率为.‎ ‎(1)请完成上面的列联表；‎ ‎(2)根据列联表的数据，若按95%的可靠性要求，能否认为“成绩与班级有关系”；‎ ‎(3)若按下面的方法从甲班优秀的学生中抽取一人：把甲班优秀的10名学生从2到11进行编号，先后两次抛掷一枚均匀的骰子，出现的点数之和为被抽取人的序号．试求抽到6号或10号的概率．‎ 附　K2＝，‎ P(K2≥k)‎ ‎0.05‎ ‎0.01‎ k ‎3.841‎ ‎6.635‎ ‎19..（本小题12分）如图所示，在三棱锥中，‎ 底面,，点分别在上，且平面.‎ ‎（Ⅰ）求证：平面;‎ ‎（Ⅱ）若，且三棱锥的体积为8，求多面体的体积。‎ ‎20.（本小题12分）已知在平面直角坐标系中，是坐标原点，动圆经过点，且与直线相切.‎ ‎（1）求动圆圆心的轨迹方程；‎ ‎（2）过的直线交曲线于两点，过作曲线的切线，直线交于点，求的面积的最小值.‎ ‎21.（本小题12分）已知函数 ‎（1）当时，求的图象在处的切线方程。‎ ‎（2）若函数在上有两个零点，求实数的取值范围 ‎22、(本小题满分10分)选修4－4：坐标系与参数方程 已知极坐标系的极点在直角坐标系的原点处，极轴与轴非负半轴重合，直线的参数方程为：为参数，)，曲线的极坐标方程为：.‎ ‎（Ⅰ）写出曲线的直角坐标方程;‎ ‎（Ⅱ）设直线与曲线相交于两点, 若，求直线的斜率.‎ 潮南实验学校高中部2017-2018学年度第二学期期中考试 ‎ 高二数学（文）答案 一、 选择题：（本大题共12小题，每小题5分，共60分.）‎ ‎1——12 CDBBD CAADA CB 二、 填空题（每题5分，满分20分）‎ ‎13——16 ，2，，‎ 三,解答题（本大题共6小题，满分12+12+12+12+12+10=70分）‎ ‎17.解　(1)∵a1＋3a2＋32a3＋…＋3n－1an＝， ①‎ ‎∴当n≥2时，‎ a1＋3a2＋32a3＋…＋3n－2an－1＝， ②‎ ‎①－②得3n－1an＝，∴an＝.‎ 在①中，令n＝1，得a1＝，适合an＝，‎ ‎∴an＝.……6分 ‎(2)∵bn＝，∴bn＝n·3n.‎ ‎∴Sn＝3＋2×32＋3×33＋…＋n·3n， ③‎ ‎∴3Sn＝32＋2×33＋3×34＋…＋n·3n＋1. ④‎ ‎③－④得－2Sn＝(3＋32＋33＋…＋3n)－n·3n＋1，‎ 即－2Sn＝－n·3n＋1，∴Sn＝＋..……12分 ‎18.解　(1)‎ 优秀 非优秀 总计 甲班 ‎10‎ ‎45‎ ‎55‎ 乙班 ‎20‎ ‎30‎ ‎50‎ 合计 ‎30‎ ‎75‎ ‎105‎ ‎………4分 ‎(2)根据列联表中的数据，得到 k＝≈6.109＞3.841，‎ 因此有95%的把握认为“成绩与班级有关系”．………8分 (3) 设“抽到6号或10号”为事件A，先后两次抛掷一枚均匀的骰子，出现的点数为 ‎(x，y)，则所有的基本事件有(1,1)、(1,2)、(1,3)、…、(6,6)，共36个．‎ 事件A包含的基本事件有(1,5)，(2,4)，(3,3)，(4,2)，(5,1)，(4,6)，(5,5)，(6,4)，共8个，‎ ‎∴P(A)＝＝.………12分 ‎19..解析：（Ⅰ）证明：因为底面，，‎ 所以...........2分 ‎ 因为，所以 ...........3分 又因为，平面............4分 ‎ 因为平面，所以 又因为平面 ，平面所以平面..........6分 ‎（Ⅱ）由题意知，平面，，，又，平面，所以，......9分 又因为.‎ 由（1）知，‎ 所以， ‎ 所以.................12分 ‎20． ……4分 ‎（2）设，直线 将代入中得 所以，，‎ 得切线： ‎ ‎……12分 ‎21、答案：（1）当时,‎ 所以切点坐标为，切线的斜率 所以所求切线方程为即 .......5分 （2） 因为，‎ 所以 因为，‎ 由，得所以在上的单调递增区间为，‎ 由，得所以在上单调减区间为 所以在处取得极大值 .......7分 又所以 所以所以在上的最小值是 .......9分 因为在上有两个零点，所以解得 所以实数的取值范围是 ......12分 ‎22.（本小题满分10分）‎ 解：（Ⅰ）， ……1分 由,得. …… 3分 所以曲线的直角坐标方程为. …… 4分 ‎（Ⅱ）把 代入，整理得 ……5分 设其两根分别为 ，则 ……6分 ‎ …… 7分 得，， …… 9分 所以直线的斜率为. …… 10分