2021届浙江新高考数学一轮复习教师用书：第九章　1 第1讲　直线的倾斜角与斜率、直线的方程 17页

知识点 最新考纲 直线的方程 理解平面直角坐标系，理解直线的倾斜角与斜率的概念，掌握直线方程的点斜式、两点式及一般式，了解直线方程与一次函数的关系.‎ 两直线的位置关系 ‎ 能根据两条直线的斜率判定这两条直线平行或垂直．‎ ‎ 会求过两点的直线斜率、两直线的交点坐标、两点间的距离、点到直线的距离、两条平行直线间的距离．‎ 圆的方程 掌握圆的标准方程与一般方程．‎ 直线、圆的位置关系 会解决直线与圆的位置关系的问题，会判断圆与圆的位置关系．‎ 椭 圆 ‎ 掌握椭圆的定义、标准方程、几何图形及简单几何性质．‎ ‎ 会解决直线与椭圆的位置关系的问题．‎ 双曲线 了解双曲线的定义、标准方程、几何图形及简单几何性质，了解直线与双曲线的位置关系．‎ 抛物线 ‎ 掌握抛物线的定义、标准方程、几何图形及简单几何性质．‎ ‎ 会解决直线与抛物线的位置关系的问题．‎ 曲线与方程 了解方程与曲线的对应关系．会求简单的曲线的方程.‎ 第1讲　直线的倾斜角与斜率、直线的方程 ‎1．直线的倾斜角 ‎(1)定义：x轴正向与直线向上方向之间所成的角叫做这条直线的倾斜角．当直线与x轴平行或重合时，规定它的倾斜角为0°．‎ ‎(2)倾斜角的范围为[0，π)．‎ ‎2．直线的斜率 ‎(1)定义：一条直线的倾斜角α的正切值叫做这条直线的斜率，斜率常用小写字母k表示，即k＝tan α，倾斜角是90°的直线没有斜率．‎ ‎(2)过两点的直线的斜率公式 经过两点P1(x1，y1)，P2(x2，y2)(x1≠x2)的直线的斜率公式为k＝＝.‎ ‎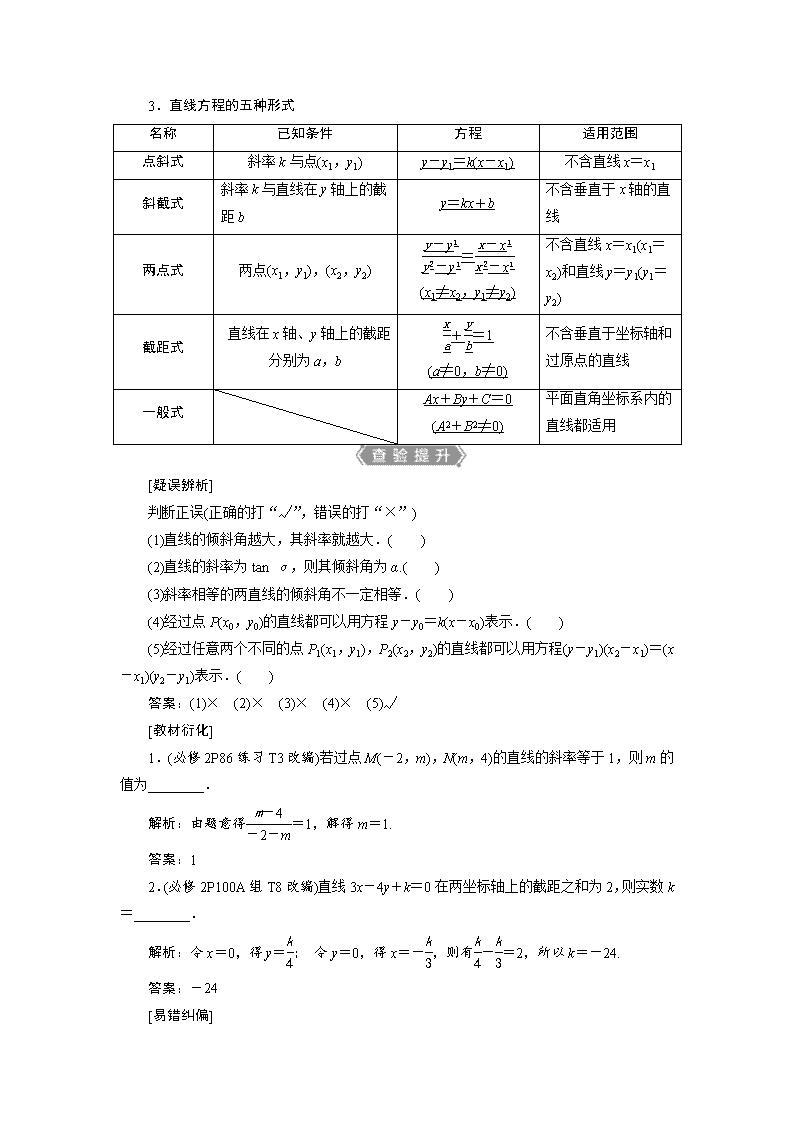3．直线方程的五种形式 名称 已知条件 方程 适用范围 点斜式 斜率k与点(x1，y1)‎ y－y1＝k(x－x1)‎ 不含直线x＝x1‎ 斜截式 斜率k与直线在y轴上的截距b y＝kx＋b 不含垂直于x轴的直线 两点式 两点(x1，y1)，(x2，y2)‎ ＝ ‎(x1≠x2，y1≠y2)‎ 不含直线x＝x1(x1＝x2)和直线y＝y1(y1＝y2)‎ 截距式 ‎ 直线在x轴、y轴上的截距分别为a，b ＋＝1‎ ‎(a≠0，b≠0)‎ 不含垂直于坐标轴和过原点的直线 一般式 Ax＋By＋C＝0‎ ‎(A2＋B2≠0)‎ 平面直角坐标系内的直线都适用 ‎[疑误辨析]‎ 判断正误(正确的打“√”，错误的打“×”)‎ ‎(1)直线的倾斜角越大，其斜率就越大．(　　)‎ ‎(2)直线的斜率为tan α，则其倾斜角为α.(　　)‎ ‎(3)斜率相等的两直线的倾斜角不一定相等．(　　)‎ ‎(4)经过点P(x0，y0)的直线都可以用方程y－y0＝k(x－x0)表示．(　　)‎ ‎(5)经过任意两个不同的点P1(x1，y1)，P2(x2，y2)的直线都可以用方程(y－y1)(x2－x1)＝(x－x1)(y2－y1)表示．(　　)‎ 答案：(1)×　(2)×　(3)×　(4)×　(5)√‎ ‎[教材衍化]‎ ‎1．(必修2P86练习T3改编)若过点M(－2，m)，N(m，4)的直线的斜率等于1，则m的值为________．‎ 解析：由题意得＝1，解得m＝1.‎ 答案：1‎ ‎2．(必修2P100A组T8改编)直线3x－4y＋k＝0在两坐标轴上的截距之和为2，则实数k＝________．‎ 解析：令x＝0，得y＝； 令y＝0，得x＝－，则有－＝2，所以k＝－24.‎ 答案：－24‎ ‎[易错纠偏]‎ ‎(1)由直线方程求斜率的思路不清；‎ ‎(2)忽视斜率和截距对直线位置的影响；‎ ‎(3)忽视直线斜率不存在的情况；‎ ‎(4)忽视截距为0的情况．‎ ‎1．直线l：xsin 30°＋ycos 150°＋a＝0的斜率为________．‎ 解析：设直线l的斜率为k，则k＝－＝.‎ 答案： ‎2．如果A·C<0且B·C<0，那么直线Ax＋By＋C＝0不通过第________象限．‎ 解析：由已知得直线Ax＋By＋C＝0在x轴上的截距－>0，在y轴上的截距－>0，故直线经过第一、二、四象限，不经过第三象限．‎ 答案：三 ‎3．过直线l：y＝x上的点P(2，2)作直线m，若直线l，m与x轴围成的三角形的面积为2，则直线m的方程为________．‎ 解析：①若直线m的斜率不存在，则直线m的方程为x＝2，直线m，直线l和x轴围成的三角形的面积为2，符合题意；②若直线m的斜率k＝0，则直线m与x轴没有交点，不符合题意；③若直线m的斜率k≠0，设其方程为y－2＝k(x－2)，令y＝0，得x＝2－，依题意有××2＝2，即＝1，解得k＝，所以直线m的方程为y－2＝(x－2)，即x－2y＋2＝0.综上可知，直线m的方程为x－2y＋2＝0或x＝2.‎ 答案：x－2y＋2＝0或x＝2‎ ‎4．过点P(2，3)且在两坐标轴上截距相等的直线方程为________．‎ 解析：当截距为0时，直线方程为3x－2y＝0；‎ 当截距不为0时，设直线方程为＋＝1，‎ 则＋＝1，解得a＝5，所以直线方程为x＋y－5＝0.‎ 答案：3x－2y＝0或x＋y－5＝0‎ ‎　　　　　　直线的倾斜角与斜率 ‎ (1)直线2xcos α－y－3＝0的倾斜角的变化范围是(　　)‎ A.　　　　　　　　 B. C. D. ‎(2)已知直线l：x－my＋m＝0上存在点M满足与两点A(－1，0)，B(1，0)连线的斜率kMA与kMB之积为3，则实数m的取值范围是(　　)‎ A．[－，]‎ B.∪ C.∪ D．以上都不对 ‎【解析】　(1)直线2xcos α－y－3＝0的斜率k＝2cos α.由于α∈，所以≤cos α≤，因此k＝2cos α∈[1，]．设直线的倾斜角为θ，则有tan θ∈[1，]．由于θ∈[0，π)，所以θ∈，即倾斜角的变化范围是.‎ ‎(2)设M(x，y)，由kMA·kMB＝3，得·＝3，即y2＝3x2－3.‎ 联立得x2＋x＋6＝0.‎ 要使直线l：x－my＋m＝0上存在点M满足与两点A(－1，0)，B(1，0)连线的斜率kMA与kMB之积为3，则Δ＝－24≥0，即m2≥.所以实数m的取值范围是∪.故选C.‎ ‎【答案】　(1)B　(2)C ‎ (变条件)若本例(1)中直线变为x＋ycos θ－3＝0(θ∈R)，则直线的倾斜角α的取值范围为________．‎ 解析：当cos θ＝0时，方程变为x－3＝0，其倾斜角为；‎ 当cos θ≠0时，由直线的方程，可得斜率k＝－.‎ 因为cos θ∈[－1，1]且cos θ≠0，‎ 所以k∈(－∞，－1]∪[1，＋∞)，‎ 即tan α∈(－∞，－1]∪[1，＋∞)，‎ 又α∈[0，π)，所以α∈∪，‎ 综上知，直线的倾斜角α的取值范围是.‎ 答案： ‎(1)求倾斜角的取值范围的一般步骤 ‎①求出斜率k＝tan α的取值范围．‎ ‎②利用三角函数的单调性，借助图象，确定倾斜角α的取值范围．‎ ‎[提醒]　求倾斜角时要注意斜率是否存在．‎ ‎(2)斜率的求法 ‎①定义法：若已知直线的倾斜角α或α的某种三角函数值，一般根据k＝tan α求斜率．‎ ‎②公式法：若已知直线上两点A(x1，y1)，B(x2，y2)，一般根据斜率公式k＝(x1≠x2)求斜率．　 ‎ ‎1．若直线l的斜率为k，倾斜角为α，且α∈∪，则k的取值范围是________．‎ 解析：当α∈时，k＝tan α∈；‎ 当α∈时，k＝tan α∈[－，0)．‎ 综上k∈[－，0)∪.‎ 答案：[－，0)∪ ‎2．若经过点P(1－a，1＋a)和Q(3，2a)的直线的倾斜角为锐角，则实数a的取值范围是________．‎ 解析：由条件知直线的斜率存在，‎ 由斜率公式得k＝.‎ 因为倾斜角为锐角，所以k>0，解得a>1或a<－2.‎ 答案：(－∞，－2)∪(1，＋∞)‎ ‎　　　　　　求直线的方程 ‎ (1)过点(－4，0)，倾斜角的正弦值为的直线方程为________．‎ ‎(2)过点M(－3，5)且在两坐标轴上的截距互为相反数的直线方程为________．‎ ‎(3)若直线过点(5，10)，且到原点的距离为5，则该直线的方程为________．‎ ‎【解析】　(1)由题设知，该直线的斜率存在，故可采用点斜式．‎ 设倾斜角为α，则sin α＝(0＜α＜π)，‎ 从而cos α＝±，则k＝tan α＝±.‎ 故所求直线方程为y＝±(x＋4)．即直线方程为x＋3y＋4＝0或x－3y＋4＝0.‎ ‎(2)①当直线过原点时，直线方程为y＝－x；‎ ‎②当直线不过原点时，设直线方程为＋＝1，‎ 即x－y＝a.代入点(－3，5)，得a＝－8.‎ 即直线方程为x－y＋8＝0.‎ 综上直线方程为y＝－x或x－y＋8＝0.‎ ‎(3)当斜率不存在时，所求直线方程为x－5＝0；‎ 当斜率存在时，设其为k，则所求直线方程为y－10＝k(x－5)，即kx－y＋(10－5k)＝0.‎ 由点线距离公式，得＝5，解得k＝.‎ 故所求直线方程为3x－4y＋25＝0.‎ 综上所求直线方程为x－5＝0或3x－4y＋25＝0.‎ ‎【答案】　(1)x＋3y＋4＝0或x－3y＋4＝0‎ ‎(2)y＝－x或x－y＋8＝0‎ ‎(3)x－5＝0或3x－4y＋25＝0‎ ‎(1)求直线方程的两种常用方法 ‎①直接法：根据已知条件，确定适当的直线方程形式，直接写出直线方程；‎ ‎②待定系数法：先设出直线方程，再根据已知条件求出待定的系数，最后代入求出直线的方程．‎ ‎(2)求直线方程应注意的问题 ‎①选择直线方程时，应注意分类讨论思想的应用：选用点斜式或斜截式时，‎ 需讨论直线的斜率是否存在；选用截距式时，需讨论直线是否过原点．‎ ‎②求直线方程时，如果没有特别要求，求出的方程应化为一般式Ax＋By＋C＝0(A，B不同时为0)．　 ‎ ‎1．已知A(－1，1)，B(3，1)，C(1，3)，则△ABC的BC边上的高所在的直线方程为(　　)‎ A．x＋y＝0‎ B．x－y＋2＝0‎ C．x＋y＋2＝0‎ D．x－y＝0‎ 解析：选B.因为B(3，1)，C(1，3)，‎ 所以kBC＝＝－1，‎ 故BC边上的高所在直线的斜率k＝1，‎ 又高线经过点A，所以其直线方程为x－y＋2＝0.‎ ‎2．过点M(－1，－2)作一条直线l，使得l夹在两坐标轴之间的线段被点M平分，则直线l的方程为________．‎ 解析：由题意，可设所求直线l的方程为y＋2＝k(x＋1)(k≠0)，直线l与x轴、y轴分别交于A、B两点，则A，B(0，k－2)．因为AB的中点为M，所以解得k＝－2.所以所求直线l的方程为2x＋y＋4＝0.‎ 答案：2x＋y＋4＝0‎ ‎　　　　　　直线方程的综合应用(高频考点)‎ 直线方程的综合应用是解析几何的一个基础内容，在高考中常与其他知识结合考查，多以选择题、填空题的形式呈现，难度为中、低档题目．主要命题角度有：‎ ‎(1)与基本不等式相结合求最值问题；‎ ‎(2)由直线方程解决参数问题．‎ 角度一　与基本不等式相结合求最值问题 ‎ (2020·杭州七校联考)直线l过点P(1，4)，分别交x轴的正半轴和y轴的正半轴于A、B两点，O为坐标原点，当|OA|＋|OB|最小时，求l的方程．‎ ‎【解】　依题意，l的斜率存在，且斜率为负，‎ 设直线l的斜率为k，‎ 则直线l的方程为y－4＝k(x－1)(k<0)．‎ 令y＝0，可得A；‎ 令x＝0，可得B(0，4－k)．‎ ‎|OA|＋|OB|＝＋(4－k)＝5－ ‎＝5＋≥5＋4＝9.‎ 所以当且仅当－k＝且k<0，‎ 即k＝－2时，|OA|＋|OB|取最小值．‎ 这时l的方程为2x＋y－6＝0.‎ ‎ (变问法)在本例条件下，若|PA|·|PB|最小，求l的方程．‎ 解：|PA|·|PB|＝ · ‎＝－(1＋k2)＝4≥8(k<0)．‎ 所以当且仅当＝－k且k<0，‎ 即k＝－1时，|PA|·|PB|取最小值．‎ 这时l的方程为x＋y－5＝0. ‎ 角度二　由直线方程解决参数问题 ‎ 已知直线l1：ax－2y＝2a－4，l2：2x＋a2y＝2a2＋4，当0＜a＜2时，直线l1，l2与两坐标轴围成一个四边形，当四边形的面积最小时，求实数a的值．‎ ‎【解】　由题意知直线l1，l2恒过定点P(2，2)，直线l1在y轴上的截距为2－a，直线l2在x轴上的截距为a2＋2，所以四边形的面积S＝×2×(2－a)＋×2×(a2＋2)＝a2－a＋4＝＋，当a＝时，面积最小．‎ 直线方程综合问题的两大类型及其解法 ‎(1)求解与直线方程有关的最值问题 先设出直线方程，建立目标函数，再利用基本不等式求解最值．‎ ‎(2)求参数值或范围 注意点在直线上，则点的坐标适合直线的方程，再结合函数的单调性或基本不等式求解．　 ‎ ‎1．直线x－2y＋b＝0与两坐标轴所围成的三角形的面积不大于1，那么b的取值范围是(　　)‎ A．[－2，2]‎ B．(－∞，－2]∪[2，＋∞)‎ C．[－2，0)∪(0，2]‎ D．(－∞，＋∞)‎ 解析：选C.令x＝0，得y＝，令y＝0，得x＝－b，‎ 所以所求三角形的面积为|－b|＝b2，且b≠0，b2≤1，所以b2≤4，所以b的取值范围是[－2，0)∪(0，2]．‎ ‎2．已知直线x＋2y＝2分别与x轴、y轴相交于A，B两点，若动点P(a，b)在线段AB上，则ab的最大值为________．‎ 解析：直线方程可化为＋y＝1，故直线与x轴的交点为A(2，0)，与y轴的交点为B(0，1)，由动点P(a，b)在线段AB上，可知0≤b≤1，且a＋2b＝2，从而a＝2－2b，故ab＝(2－2b)b＝－2b2＋2b＝－2＋，由于0≤b≤1，故当b＝时，ab取得最大值.‎ 答案： 核心素养系列18　直观想象——巧构造，妙用斜率求解问题 一、比较大小 ‎ 已知函数f(x)＝log2(x＋1)，且a>b>c>0，则，，的大小关系为________．‎ ‎【解析】　作出函数f(x)＝log2(x＋1)的大致图象，如图所示，可知当x>0时，曲线上各点与原点连线的斜率随x的增大而减小，‎ 因为a>b>c>0，‎ 所以<<.‎ ‎【答案】　<< 对于函数f(x)图象上的两点(a，f(a))，(b，f(b))，比较与的大小时，可转化为这两点与原点连线的斜率来比较大小．　 ‎ 二、求最值 ‎ 已知实数x，y满足y＝x2－2x＋2(－1≤x≤1)，试求的最大值和最小值．‎ ‎【解】　如图，作出y＝x2－2x＋2(－1≤x≤1)的图象(曲线段AB)，则表示定点P(－2，－3)和曲线段AB上任一点(x，y)的连线的斜率k，连接PA，PB，则kPA≤k≤kPB.‎ 易得A(1，1)，B(－1，5)，所以kPA＝＝，kPB＝＝8，所以≤k≤8，故的最大值是8，最小值是.‎ 对于求形如k＝，y＝的最值问题，可利用定点与动点的相对位置，转化为求直线斜率的范围，借助数形结合进行求解．　 ‎ 三、证明不等式 ‎ 已知a，b，m∈(0，＋∞)，且a.‎ ‎【证明】　如图，设点P，M的坐标分别为(b，a)，(－m，－m)．‎ 因为00，所以点M在第三象限，且在直线y＝x上．‎ 连接OP，PM，则kOP＝，kMP＝.‎ 因为直线MP的倾斜角大于直线OP的倾斜角，且两条直线的倾斜角都是锐角，‎ 所以kMP>kOP，即>.‎ 根据所证不等式的特点，寻找与斜率公式有关的信息，从而转变思维角度，构造直线斜率解题，这也是解题中思维迁移的一大技巧，可取得意想不到的效果．　 ‎ ‎ [基础题组练]‎ ‎1．(2020·丽水模拟)倾斜角为120°，在x轴上的截距为－1的直线方程是(　　)‎ A.x－y＋1＝0　　　　　 B.x－y－＝0‎ C.x＋y－＝0 D.x＋y＋＝0‎ 解析：选D.由于倾斜角为120°，故斜率k＝－.又直线过点(－1，0)，所以方程为y＝－(x＋1)，即x＋y＋＝0.‎ ‎2．已知直线l的斜率为，在y轴上的截距为另一条直线x－2y－4＝0的斜率的倒数，则直线l的方程为(　　)‎ A．y＝x＋2 B．y＝x－2‎ C．y＝x＋ D．y＝－x＋2‎ 解析：选A.因为直线x－2y－4＝0的斜率为，‎ 所以直线l在y轴上的截距为2，‎ 所以直线l的方程为y＝x＋2.‎ ‎3．直线xsin 2－ycos 2＝0的倾斜角的大小是(　　)‎ A．－ B．－2‎ C. D．2‎ 解析：选D.因为直线xsin 2－ycos 2＝0的斜率k＝＝tan 2，所以直线的倾斜角为2.‎ ‎4．已知函数f(x)＝ax(a＞0且a≠1)，当x＜0时，f(x)＞1，方程y＝ax＋表示的直线是(　　)‎ 解析：选C.因为x＜0时，ax＞1，所以0＜a＜1.‎ 则直线y＝ax＋的斜率0＜a＜1，‎ 在y轴上的截距＞1.故选C.‎ ‎5．(2020·温州质检)若直线l与直线y＝1，x＝7分别交于点P，Q，且线段PQ的中点坐标为(1，－1)，则直线l的斜率为(　　)‎ A. B．－ C．－ D. 解析：选B.依题意，设点P(a，1)，Q(7，b)，则有解得a＝－5，b＝－3，从而可知直线l的斜率为＝－.‎ ‎6．过点(5，2)，且在y轴上的截距是在x轴上的截距的2倍的直线方程是(　　)‎ A．2x＋y－12＝0‎ B．2x＋y－12＝0或2x－5y＝0‎ C．x－2y－1＝0‎ D．x－2y－1＝0或2x－5y＝0‎ 解析：选B.当直线过原点时，由直线过点(5，2)，可得直线的斜率为，故直线的方程为y＝x，即2x－5y＝0.当直线不过原点时，设直线在x轴上的截距为k(k≠0)，则在y轴上的截距是2k，直线的方程为＋＝1，把点(5，2)代入可得＋＝1，解得k＝6.故直线的方程为＋＝1，即2x＋y－12＝0.‎ ‎7．过点A(－1，－3)，斜率是直线y＝3x的斜率的－的直线方程为________．‎ 解析：设所求直线的斜率为k，依题意 k＝－×3＝－.‎ 又直线经过点A(－1，－3)，‎ 因此所求直线方程为y＋3＝－(x＋1)，‎ 即3x＋4y＋15＝0.‎ 答案：3x＋4y＋15＝0‎ ‎8．若点A(4，3)，B(5，a)，C(6，5)三点共线，则a的值为________．‎ 解析：因为kAC＝＝1，kAB＝＝a－3.‎ 由于A，B，C三点共线，所以a－3＝1，即a＝4.‎ 答案：4‎ ‎9．设点A(－1，0)，B(1，0)，直线2x＋y－b＝0与线段AB相交，则b的取值范围是________．‎ 解析：b为直线y＝－2x＋b在y轴上的截距，‎ 如图，当直线y＝－2x＋b过点A(－1，0)和点B(1，0)时b分别取得最小值和最大值．‎ 所以b的取值范围是[－2，2]．‎ 答案：[－2，2]‎ ‎10．一条直线经过点A(－2，2)，并且与两坐标轴围成的三角形的面积为1，则此直线的方程为________________．‎ 解析：设所求直线的方程为＋＝1，‎ 因为A(－2，2)在直线上，所以－＋＝1.①‎ 又因为直线与坐标轴围成的三角形面积为1，‎ 所以|a|·|b|＝1.②‎ 由①②可得(1)或(2) 由(1)解得或方程组(2)无解．‎ 故所求的直线方程为＋＝1或＋＝1，‎ 即x＋2y－2＝0或2x＋y＋2＝0为所求直线的方程．‎ 答案：x＋2y－2＝0或2x＋y＋2＝0‎ ‎11．设直线l的方程为x＋my－2m＋6＝0，根据下列条件分别确定m的值：‎ ‎(1)直线l的斜率为1；‎ ‎(2)直线l在x轴上的截距为－3.‎ 解：(1)因为直线l的斜率存在，所以m≠0，‎ 于是直线l的方程可化为y＝－x＋.‎ 由题意得－＝1，解得m＝－1.‎ ‎(2)法一：令y＝0，得x＝2m－6.‎ 由题意得2m－6＝－3，解得m＝.‎ 法二：直线l的方程可化为x＝－my＋2m－6.由题意得2m－6＝－3，解得m＝.‎ ‎12．已知直线l：kx－y＋1＋2k＝0(k∈R)．若直线l交x轴负半轴于A，交y轴正半轴于B，△AOB的面积为S(O为坐标原点)，求S的最小值并求此时直线l的方程．‎ 解：由l的方程，得A，B(0，1＋2k)．‎ 依题意得 解得k＞0.‎ 因为S＝·|OA|·|OB|‎ ‎＝··|1＋2k|‎ ‎＝·＝ ‎≥×(2×2＋4)＝4，‎ ‎“＝”成立的条件是k＞0且4k＝，‎ 即k＝，所以Smin＝4，‎ 此时直线l的方程为x－2y＋4＝0.‎ ‎[综合题组练]‎ ‎1．(2020·富阳市场口中学高三质检)已知点A(2，－3)、B(－3，－2)，直线l过点P(1，1)，且与线段AB相交，则直线l的斜率k的取值范围是(　　)‎ A．k≥或k≤－4 B．k≥或k≤－ C．－4≤k≤ D.≤k≤4‎ 解析：选A.如图所示，由题意得，所求直线l的斜率k满足k≥kPB或k≤kPA，即k≥或k≤－4，故选A.‎ ‎2．已知动直线l：ax＋by＋c－2＝0(a＞0，c＞0)恒过点P(1，m)且Q(4，0)到动直线l的最大距离为3，则＋的最小值为(　　)‎ A. B. C．1 D．9‎ 解析：选B.因为动直线l：ax＋by＋c－2＝0(a＞0，c＞0)恒过点P(1，m)，所以a＋bm＋c－2＝0，又Q(4，0)到动直线l的最大距离为3，所以＝3，解得m＝0‎ ‎，所以a＋c＝2，则＋＝(a＋c)·＝≥＝，当且仅当c＝2a＝时取等号，故选B.‎ ‎3．(2020·金丽衢十二校高考模拟)直线l：x＋λy＋2－3λ＝0(λ∈R)恒过定点________，P(1，1)到该直线的距离的最大值为________．‎ 解析：直线l：x＋λy＋2－3λ＝0(λ∈R)即λ(y－3)＋x＋2＝0，令，解得x＝－2，y＝3.‎ 所以直线l恒过定点Q(－2，3)，‎ P(1，1)到该直线的距离最大值为|PQ|＝＝.‎ 答案：(－2，3)　 ‎4．直线l的倾斜角是直线4x＋3y－1＝0的倾斜角的一半，若l不过坐标原点，则l在x轴上与y轴上的截距之比为________．‎ 解析：设直线l的倾斜角为θ.所以tan 2θ＝－.‎ ＝－，所以tan θ＝2或tan θ＝－，‎ 由2θ∈[0°，180°)知，θ∈[0°，90°)．‎ 所以tan θ＝2.‎ 又设l在x轴上的截距为a，在y轴上的截距为b.‎ 所以tan θ＝－.即＝－＝－.‎ 答案：－ ‎5.如图，射线OA，OB分别与x轴正半轴成45°和30°角，过点P(1，0)作直线AB分别交OA，OB于A，B两点，当AB的中点C恰好落在直线y＝x上时，求直线AB的方程．‎ 解：由题意可得kOA＝tan 45°＝1，‎ kOB＝tan(180°－30°)＝－，‎ 所以直线lOA：y＝x，lOB：y＝－x.‎ 设A(m，m)，B(－n，n)，‎ 所以AB的中点C，‎ 由点C在直线y＝x上，且A，P，B三点共线得 解得m＝，所以A(，)．‎ 又P(1，0)，所以kAB＝kAP＝＝，‎ 所以lAB：y＝(x－1)，‎ 即直线AB的方程为(3＋)x－2y－3－＝0.‎ ‎6．为了绿化城市，拟在矩形区域ABCD内建一个矩形草坪(如图)，另外△EFA内部有一文物保护区不能占用，经测量AB＝100 m，BC＝80 m，AE＝30 m，AF＝20 m，应如何设计才能使草坪面积最大？‎ 解：如图所示，建立平面直角坐标系，则E(30，0)，F(0，20)，‎ 所以直线EF的方程为＋＝1(0≤x≤30)．‎ 易知当矩形草坪的一个顶点在EF上时，可取最大值，‎ 在线段EF上取点P(m，n)，作PQ⊥BC于点Q，‎ PR⊥CD于点R，设矩形PQCR的面积为S，‎ 则S＝|PQ|·|PR|＝(100－m)(80－n)．‎ 又＋＝1(0≤m≤30)，所以n＝20－m.‎ 所以S＝(100－m) ‎＝－(m－5)2＋(0≤m≤30)．‎ 所以当m＝5时，S有最大值，这时＝5∶1.‎ 所以当矩形草坪的两边在BC，CD上，一个顶点在线段EF上，且这个顶点分有向线段EF成5∶1时，草坪面积最大．‎