高考数学专题复习课件：1-2 命题及其关系、充分条件与必要条件 45页

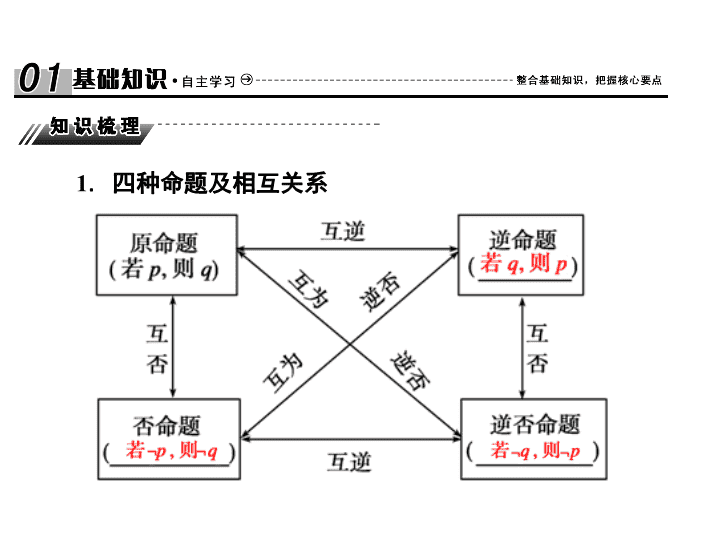
§1.2 　命题及其关系、充分条件与必要条件 [ 考纲要求 ] 　 1. 理解命题的概念 .2. 了解 “ 若 p ，则 q ” 形式的命题及其逆命题、否命题与逆否命题，会分析四种命题的相互关系 .3. 理解必要条件、充分条件与充要条件的含义． 1 ． 四种命题及相互关系 2 ． 四种命题的真假关系 (1) 两个命题互为逆否命题，它们有 ______ 的真假性，在四种形式的命题中真命题的个数只能是 0 ， 2 或 4 ； (2) 两个命题互为逆命题或互为否命题，它们的真假性没有关系． 相同 3 ． 充分条件与必要条件 (1) 如果 p ⇒ q ，则 p 是 q 的 ______ 条件，同时 q 是 p 的 ______ 条件； (2) 如果 p ⇒ q ，但 q p ，则 p 是 q 的 ___________ 条件； (3) 如果 p ⇒ q ，且 q ⇒ p ，则 p 是 q 的 _______ 条件； (4) 如果 q ⇒ p ，且 p q ，则 p 是 q 的 ___________ 条件； (5) 如果 p q ，且 q p ，则 p 是 q 的既不充分又不必要条件． 必要 充分不必要 充要 必要不充分 充分 (3) 若一个命题是真命题，则其逆否命题是真命题． ( 　　 ) (4) 当 q 是 p 的必要条件时， p 是 q 的充分条件． ( 　　 ) (5) 当 p 是 q 的充要条件时，也可说成 q 成立当且仅当 p 成立． ( 　　 ) (6) 若 p 是 q 的充分不必要条件，则 綈 p 是 綈 q 的必要不充分条件． ( 　　 ) 【 答案 】 (1) × 　 (2) × 　 (3) √ 　 (4) √ 　 (5) √ 　 (6) √ 1 ． (2017· 河北邯郸一中研六考试 ) “ x ＜ 0 ” 是 “ ln( x ＋ 1) ＜ 0 ” 的 ( 　　 ) A ．必要不充分条件 B ．充分不必要条件 C ．充要条件 D ．既不充分也不必要条件 【 解析 】 因为 ln( x ＋ 1) ＜ 0 ，所以 ln( x ＋ 1) ＜ ln 1 ，即－ 1 ＜ x ＜ 0 ，因而 “ x ＜ 0 ” 是 “ ln( x ＋ 1) ＜ 0 ” 的必要不充分条件． 【 答案 】 A 2 ． (2016· 山东 ) 已知直线 a ， b 分别在两个不同的平面 α ， β 内，则 “ 直线 a 和直线 b 相交 ” 是 “ 平面 α 和平面 β 相交 ” 的 ( 　　 ) A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分也不必要条件 【 解析 】 若直线 a ， b 相交，则平面 α ， β 一定相交；反之，若平面 α ， β 相交，且 a ⊂ α ， b ⊂ β ，则 a 与 b 不一定相交．因此 “ 直线 a 和直线 b 相交 ” 是 “ 平面 α 与平面 β 相交 ” 的充分不必要条件．故选 A. 【 答案 】 A 【 答案 】 B 4 ．已知集合 A ＝ {1 ， a } ， B ＝ {1 ， 2 ， 3} ，则 “ a ＝ 3 ” 是 “ A ⊆ B ” 的 ( 　　 ) A ．充分而不必要条件 B ．必要而不充分条件 C ．充分必要条件 D ．既不充分也不必要条件 【 解析 】 a ＝ 3 时 A ＝ {1 ， 3} ，显然 A ⊆ B . 但 A ⊆ B 时， a ＝ 2 或 3. 所以 A 正确． 【 答案 】 A 5 ． ( 教材改编 ) 下列命题： ① x ＝ 2 是 x 2 － 4 x ＋ 4 ＝ 0 的必要不充分条件； ② 圆心到直线的距离等于半径是这条直线为圆的切线的充分必要条件； ③ sin α ＝ sin β 是 α ＝ β 的充要条件； ④ ab ≠ 0 是 a ≠ 0 的充分不必要条件． 其中为真命题的是 ________( 填序号 ) ． 【 答案 】 ②④ 题型一　命题及其关系 【 例 1 】 (1) 命题 “ 若 x ， y 都是偶数，则 x ＋ y 也是偶数 ” 的逆否命题是 ( 　　 ) A ．若 x ＋ y 是偶数，则 x 与 y 不都是偶数 B ．若 x ＋ y 是偶数，则 x 与 y 都不是偶数 C ．若 x ＋ y 不是偶数，则 x 与 y 不都是偶数 D ．若 x ＋ y 不是偶数，则 x 与 y 都不是偶数 (2) 原命题为 “ 若 z 1 ， z 2 互为共轭复数，则 | z 1 | ＝ | z 2 | ” ，关于其逆命题，否命题，逆否命题真假性的判断依次如下，正确的是 ( 　　 ) A ．真，假，真　　　　　 B ．假，假，真 C ．真，真，假 D ．假，假，假 【 解析 】 (1) 由于 “ x ， y 都是偶数 ” 的否定表达是 “ x ， y 不都是偶数 ” ， “ x ＋ y 是偶数 ” 的否定表达是 “ x ＋ y 不是偶数 ” ，故原命题的逆否命题为 “ 若 x ＋ y 不是偶数，则 x ， y 不都是偶数 ” ． 【 答案 】 (1)C 　 (2)B 【 方法规律 】 (1) 写一个命题的其他三种命题时，需注意： ① 对于不是 “ 若 p ，则 q ” 形式的命题，需先改写； ② 若命题有大前提，写其他三种命题时需保留大前提． (2) 判断一个命题为真命题，要给出推理证明；判断一个命题是假命题，只需举出反例． (3) 根据 “ 原命题与逆否命题同真同假，逆命题与否命题同真同假 ” 这一性质，当一个命题直接判断不易进行时，可转化为判断其等价命题的真假． (2) (2017· 承德二模 ) 已知命题 α ：如果 x ＜ 3 ，那么 x ＜ 5 ；命题 β ：如果 x ≥ 3 ，那么 x ≥ 5 ；命题 γ ：如果 x ≥ 5 ，那么 x ≥ 3. 关于这三个命题之间的关系，下列三种说法正确的是 ( 　　 ) ① 命题 α 是命题 β 的否命题，且命题 γ 是命题 β 的逆命题； ② 命题 α 是命题 β 的逆命题，且命题 γ 是命题 β 的否命题； ③ 命题 β 是命题 α 的否命题，且命题 γ 是命题 α 的逆否命题． A ． ①③ B ． ② C ． ②③ D ． ①②③ 【 答案 】 (1)C 　 (2)A 题型二　充分必要条件的判定 【 例 2 】 (1) (2015· 四川 ) 设 a ， b 都是不等于 1 的正数，则 “ 3 a ＞ 3 b ＞ 3 ” 是 “ log a 3 ＜ log b 3 ” 的 ( 　　 ) A ．充要条件 B ．充分不必要条件 C ．必要不充分条件 D ．既不充分也不必要条件 【 答案 】 (1)B 　 (2)A 【 方法规律 】 充要条件的三种判断方法 (1) 定义法：根据 p ⇒ q ， q ⇒ p 进行判断． (2) 集合法：根据 p ， q 成立的对应的集合之间的包含关系进行判断． (3) 等价转化法：根据一个命题与其逆否命题的等价性，把判断的命题转化为其逆否命题进行判断．这个方法特别适合以否定形式给出的问题，常用的是逆否等价法． 跟踪训练 2 (1) (2015· 陕西 ) “ sin α ＝ cos α ” 是 “ cos 2 α ＝ 0 ” 的 ( 　　 ) A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件 D ．既不充分也不必要条件 【 答案 】 (1)A 　 (2)A 题型三　充分必要条件的应用 【 例 3 】 (1) (2017· 南昌模拟 ) 已知条件 p ： | x － 4| ≤ 6 ；条件 q ： ( x － 1) 2 － m 2 ≤ 0( m ＞ 0) ，若 p 是 q 的充分不必要条件，则 m 的取值范围是 ( 　　 ) A ． [21 ，＋ ∞ ) B ． [9 ，＋ ∞ ) C ． [19 ，＋ ∞ ) D ． (0 ，＋ ∞ ) (2) 已知 P ＝ { x | x 2 － 8 x － 20 ≤ 0} ，非空集合 S ＝ { x |1 － m ≤ x ≤ 1 ＋ m } ．若 x ∈ P 是 x ∈ S 的必要条件，则 m 的取值范围为 ________ ． 【 答案 】 (1)B 　 (2)[0 ， 3] 探究 1 本例 (2) 条件不变，问是否存在实数 m ，使 x ∈ P 是 x ∈ S 的充要条件． 探究 2 本例 (2) 条件不变，若 綈 P 是 綈 S 的必要不充分条件，求实数 m 的取值范围． 【 方法规律 】 充分条件、必要条件的应用，一般表现在参数问题的求解上．解题时需注意： (1) 把充分条件、必要条件或充要条件转化为集合之间的关系，然后根据集合之间的关系列出关于参数的不等式 ( 或不等式组 ) 求解． (2) 要注意区间端点值的检验． 跟踪训练 3 (1) ax 2 ＋ 2 x ＋ 1 ＝ 0 至少有一个负实根的充要条件是 ( 　　 ) A ． 0 ＜ a ≤ 1 B ． a ＜ 1 C ． a ≤ 1 D ． 0 ＜ a ≤ 1 或 a ＜ 0 (2) (2017· 安徽望江中学调研 ) 已知条件 p ： 2 x 2 － 3 x ＋ 1 ≤ 0 ，条件 q ： x 2 － (2 a ＋ 1) x ＋ a ( a ＋ 1) ≤ 0. 若 綈 p 是 綈 q 的必要不充分条件，则实数 a 的取值范围是 ________ ． 思想与方法系列 1 等价转化思想在充要条件中的应用 【 典例 】 (1) 已知 p ： ( a － 1) 2 ≤ 1 ， q ： ∀ x ∈ R ， ax 2 － ax ＋ 1 ≥ 0 ，则 p 是 q 成立的 ( 　　 ) A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分也不必要条件 (2) 已知条件 p ： x 2 ＋ 2 x － 3 ＞ 0 ；条件 q ： x ＞ a ，且 綈 q 的一个充分不必要条件是 綈 p ，则 a 的取值范围是 ( 　　 ) A ． [1 ，＋ ∞ ) B ． ( － ∞ ， 1] C ． [ － 1 ，＋ ∞ ) D ． ( － ∞ ，－ 3] 【 答案 】 (1)A 　 (2)A 【 温馨提醒 】 (1) 本题用到的等价转化 ① 将 綈 p ， 綈 q 之间的关系转化成 p ， q 之间的关系． ② 将条件之间的关系转化成集合之间的关系． (2) 对一些复杂、生疏的问题，利用等价转化思想转化成简单、熟悉的问题，在解题中经常用到 . ► 方法与技巧 1 ．写出一个命题的逆命题、否命题及逆否命题的关键是分清原命题的条件和结论，然后按定义来写；在判断原命题、逆命题、否命题以及逆否命题的真假时，要借助原命题与其逆否命题同真或同假，逆命题与否命题同真或同假来判定． 2 ．充要条件的几种判断方法 (1) 定义法：直接判断若 p 则 q 、若 q 则 p 的真假． ► 失误与防范 1 ．当一个命题有大前提而要写出其他三种命题时，必须保留大前提． 2 ．判断命题的真假及写四种命题时，一定要明确命题的结构，可以先把命题改写成 “ 若 p ，则 q ” 的形式． 3 ．判断条件之间的关系要注意条件之间关系的方向，正确理解 “ p 的一个充分而不必要条件是 q ” 等语言 .