- 262.73 KB
- 2021-06-10 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
高一数学 第 1 页 共 5 页
成都市郫都区 2020-2021学年度上期期中考试
高 一 数 学
命题人:孙卉 审题人:胥智 任后兵
说明:1.本卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分 150分,时间 120分钟.
2. 所有试题均在答题卡相应的区域内作答.
第 I卷(选择题 共 60分)
一、选择题(本大题共 12 小题,每小题 5 分,共 60 分,在每小题给出的四个选项中,
只有一项是最符合题目要求的)
1.已知集合 A={x|x<1},B={x| 3 1x },则
A. { | 1}A B x x B. A B R
C. { | 0}A B x x D. A B
2.设全集为U ,集合 1,3,5,7,9A , 1,2,3,4,5B ,则图中阴影部分表示的集合是( )
A. 5,3,1 B. 1,2,3,4,5
C. 2,4 D. 7,9
3.下列各组函数中,表示同一个函数的是( ).
A. 1f x , 0g x x B. 2f x x ,
2 4
2
xg x
x
C. f x x , 2g x x D. f x x , 2g x x
4.函数
1( )
2
xy 的大致图像是( )
A. B. C. D.
高一数学 第 2 页 共 5 页
5.函数
1 1, 0
2( )
1 , 0
x x
f x
x
x
,若 ( )f a a ,则实数 a的值为( )
A. 1 B. 2 1 或 C. 2 1 或 D. 1
6.设
0.34
5
a
,
0.25
4
b
, 1
2
5log
4
c ,则 a、b、 c的大小关系为( )
A. b a c B. a b c C. c b a D. b c a
7.函数 ( )f x 在 ( , ) 单调递减,且为奇函数.若 ( 11)f ,则满足 21 ( ) 1xf
的 x的取值范围是( )
A.[ 2,2] B.[ 1,1] C.[0, 4] D.[1,3]
8.函数 y= 9-x2
log2x+1
的定义域是( )
A.(-1,3) B.(-1,3]
C.(-1,0) (0,3) D.(-1,0) (0,3]
9.设 2log 3a ,则 6log 12可表示为( )
A. 1
2
a
a
B. 2
1
a
a
C. 1
2
a
a
D. 2
1
a
a
10.定义在R上的运算“”:
, ,
, ,
a a b
a b
b a b
,设函数 2( ) 2 2 1 logxf x x ,
(0,2)x ,则 ( )f x 的值域为( )
A. (0,3) B.[0,3) C. [1,3) D. (1,3)
11.已知函 2
2020( ) 2020 log ( 1 ) 2020 2x xf x x x ,则关于 x的不等式
3 1 4f x f x 的解集为( )
A. 1 ,
4
B. 1,
4
C. 0, D. ,0
高一数学 第 3 页 共 5 页
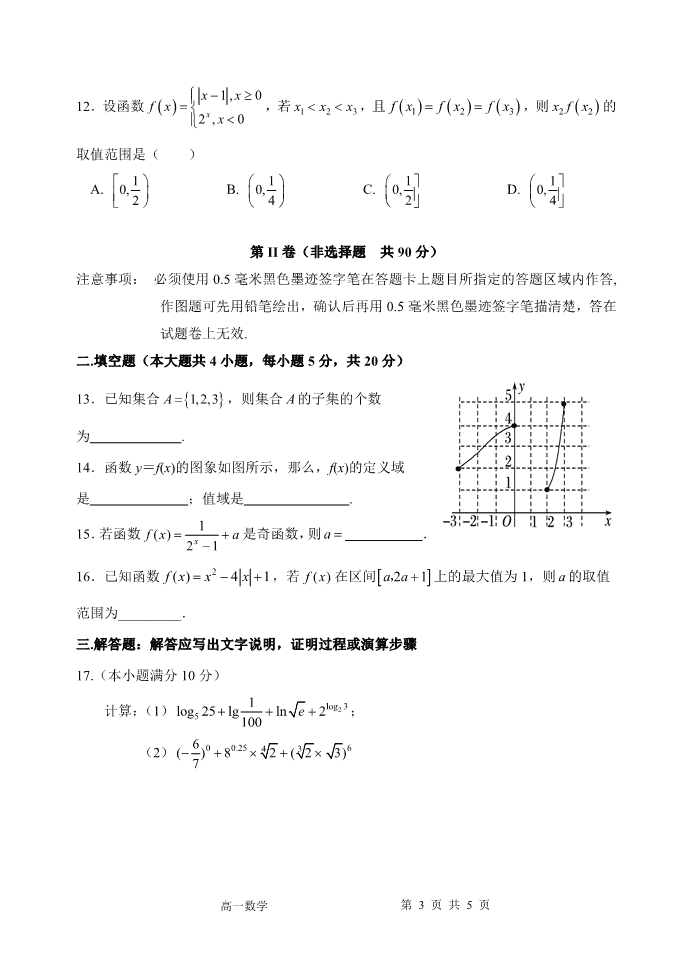
12.设函数
1 , 0
2 , 0x
x x
f x
x
,若 1 2 3x x x ,且 1 2 3f x f x f x ,则 2 2x f x 的
取值范围是( )
A. 10,
2
B. 10,
4
C. 10,
2
D. 10,
4
第 II卷(非选择题 共 90分)
注意事项: 必须使用 0.5毫米黑色墨迹签字笔在答题卡上题目所指定的答题区域内作答,
作图题可先用铅笔绘出,确认后再用 0.5毫米黑色墨迹签字笔描清楚,答在
试题卷上无效.
二.填空题(本大题共 4小题,每小题 5分,共 20分)
13.已知集合 1,2,3A ,则集合 A的子集的个数
为 .
14.函数 y=f(x)的图象如图所示,那么,f(x)的定义域
是 ;值域是 .
15.若函数
1( )
2 1xf x a
是奇函数,则 a .
16.已知函数 2( ) 4 1f x x x ,若 ( )f x 在区间 2 1a a , 上的最大值为 1,则 a的取值
范围为_________.
三.解答题:解答应写出文字说明,证明过程或演算步骤
17.(本小题满分 10分)
计算:(1) 2log 3
5
1log 25 lg ln 2
100
e ;
(2) 0 0.25 6346( ) 8 2 ( 2 3)
7
高一数学 第 4 页 共 5 页
18.(本小题满分 12分)
已知全集 { | 6 5}U x x ,
1{ | 2 4}
8
xM x , { | 0 2}N x x .
(1)求 ( )UM C N ;
(2)若 { | 2 1}C x a x a 且C M M ,求 a的取值范围.
19.(本小题满分 12分)
已知函数 1f x x
x
.
(1)请判断函数 f x 在 0,1 和 (1, ) 内的单调性,并用定义证明在 0,1 的单调性;
(2)当
1 1,
4 2
x
时, 2 1 0x ax 恒成立,求实数 a的取值范围.
20.(本小题满分 12分)
设函数 1log 1
2af x x
, 1log 1
2ag x x
( 0a 且 1a ),若
h x f x g x .
(1)求函数 h x 的定义域;
(2)判断 h x 的奇偶性,并说明理由;
(3)求使 0h x 成立的 x的集合.
高一数学 第 5 页 共 5 页
21.(本小题满分 12分)
经市场调查,某商品在过去的 100天内的日销售量(单位:件)和价格(单位:元)均为时间
t (单位:天)的函数,且日销售量 ( )f t 满足
60 , 1 60
( ) , 1 100,1150 , 61 100
2
t t
f t t t
t t
N ,
价格 g t 满足 g t = 200 1 100,t t t N .
(1)求该种商品的日销售额 h t 与时间 t的函数关系;
(2)若销日售额超过 16610元,商家认为该商品的收益达到理想程度,请判断该商
品在这 100天中的哪几天收益达到理想程度?
22.(本小题满分 12分)
已知函数 y f x ,若在定义域内存在 0x ,使得 0 0f x f x 成立,则称 0x 为
函数 f x 的局部对称点.
(1)若 , 0a a R ,证明:函数 2f x ax x a 必有局部对称点;
(2)若函数 1 24 2 3x xf x m m 在R上有局部对称点,求实数m的取值范围.