高中数学选修2-2课件数学：第一章《导数及其应用》课件（1）（新人教A版选修2-2） 31页

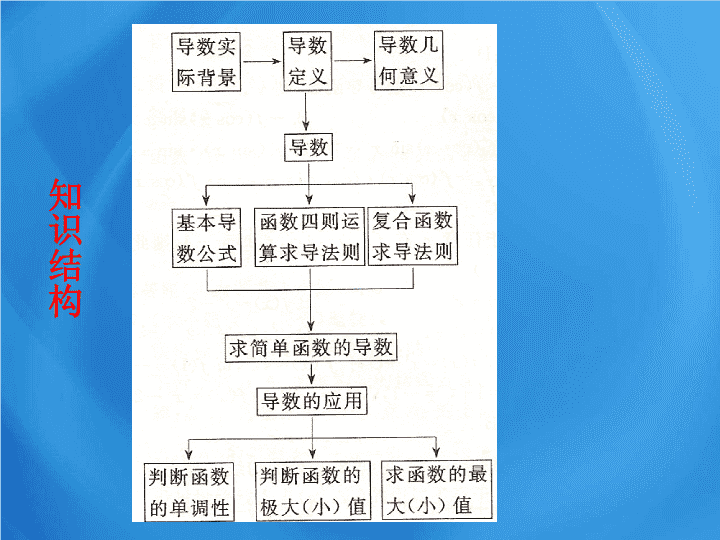
导数及其应用 知识结构 Ⅰ 、导数的概念 Ⅱ 、几种常见函数的导数公式 Ⅲ 、求导法则 Ⅳ 、复合函数求导 Ⅴ 、导数的几何意义 Ⅵ 、导数的应用 1 ．判断函数的单调性 2 ．求函数的极值 3 ．求函数的最值 例 2 ：用公式法求下列导数： （ 1 ） y= （ 3 ） y=ln(x+sinx) （ 2 ） y= （ 4 ） y= 解 (1) y′= (2) (3) (4) 例 3 、已知 f ( x ) =2x 2 +3x f  ( 1 ) , f  ( 0 )= 解 : 由已知得 : f  ( x ) =4x+3 f  ( 1 ) , ∴ f  ( 1 ) =4+3 f  ( 1 ) , ∴ f  ( 1 ) = - 2 ∴ f  ( 0 ) = 4×0+3 f  ( 1 ) =3×(-2)=-6 例 4 （ 2001 文）已知函数 f(x)=x 3 -3ax 2 +2bx 在点 x=1 处有极小值 -1 ，试确定 a 、 b 的值，并求出 f(x) 的单调区间。 分析： f(x) 在 x=1 处有极小值 -1 ，意味着 f(1)=-1 且 f`(1)=0 ，故取点可求 a 、 b 的值，然后根据求函数单调区间的方法，求出单调区间 。 略 解： 单增区间为（ -∞ ， -1/3 ）和（ 1 ， +∞ ） 单间区间为（ -1/3 ， 1 ） 练习巩固： 设函数 y=x 3 +ax 2 +bx+c 的图象如图所示，且与 y=0 在原点相切，若函数的极小值为 -4 （ 1 ）求 a 、 b 、 c 的值 （ 2 ）求函数的单调区间 答案（ 1 ） a=-3,b=0,c=0 （ 2 ）单增区间为 (-∞,0) 和 (2,+∞) 解 : 由已知 , 函数 f ( x ) 过原点 (0,0), ∴ f ( 0 ) =c=0 ∵ f  ( x )=3x 2 +2ax+b 且函数 f ( x ) 与 y=0 在原点相切， ∴ f  ( 0 )=b=0 即 f ( x )=x 3 +ax 2 由 f  ( x )=3x 2 +2ax=0, 得 x 1 =0,x 2 =(-2/3)a 由已知 即 解得 a=-3 小结： 利用导数的几何意义求切线的斜率； 求函数的单调区间，只要解不等式 f(x) ＞ 0 或 f(x) ＜ 0 即可； 求函数 f(x) 的极值，首先求 f `(x), 在求 f ` (x)=0 的根，然后检查方程根左右两侧的导数符号而作出判定； 函数 f(x) 在［ a,b ］内的最值求法：①求 f(x) 在（ a,b ）内的极值；②将 f(x) 的各极值与 f(a),f(b) 比较，其中最大的是最大值，最小的为最小值。 导数的应用主要表现在： 定积分及其应用 1 、求曲边梯形的思想方法是什么？ 2 、定积分的几何意义、物理是什么？ 3 、微积分基本定理是什么？ 求由连续曲线 y = f ( x ) 对应的 曲边梯形 面积的方法 (2) 取近似求和 : 任取 x i  [ x i - 1 , x i ] ，第 i 个小曲边梯形的面积用高为 f ( x i ) 而宽为 D x 的小矩形面积 f ( x i ) D x 近似之。 (3) 取极限 : ， 所求曲边 梯形的面积 S 为 取 n 个小矩形面积的和作为曲边梯形面积 S 的近似值： x i y = f ( x ) x y O b a x i +1 x i (1) 分割 : 在区间 [0,1] 上等间隔地插入 n-1 个点 , 将它等分成 n 个小区间 : 每个小区间宽度⊿ x 定积分的定义 如果当 n  ∞ 时， S 的无限接近某个常数， 这个常数为函数 f ( x ) 在区间 [ a , b ] 上的定积分，记作 从求曲边梯形面积 S 的过程中可以看出 , 通过 “四步曲” : 分割 --- 近似代替 ---- 求和 ------ 取极限得到解决 . 定积分的定义 ： 定积分的相关名称：  ——— 叫做积分号， f ( x ) —— 叫做被积函数， f ( x ) dx — 叫做被积表达式， x ——— 叫做积分变量， a ——— 叫做积分下限， b ——— 叫做积分上限， [ a , b ] — 叫做积分区间。 被积函数 被积表达式 积分变量 积分下限 积分上限 按定积分的定义，有 (1) 由连续曲线 y = f ( x ) ( f ( x )  0) ，直线 x = a 、 x = b 及 x 轴所围成的曲边梯形的面积为 (2) 设物体运动的速度 v = v ( t ) ，则此物体在时间区间 [ a , b ] 内运动的距离 s 为 定积分的定义： 例 1 、求曲线 与直线 x 轴所围成的图形面积。 略解：根据定积分的几何意义所求面积为 （ 一）利用定积分求平面图形的面积 平面图形的面积 平面图形的面积 平面图形的面积 平面图形的面积 平面图形的面积 特别注意图形面积与定积分不一定相等 , 的图像与 轴围成的图形的面积为 4, 而其定积分为 0. 如函数 1 、求直线 与抛物线 所围成的图形面积。 略解：如图直线 与抛物线 的交点 坐标为（－ 1 ， 1 ） 和（ 3 ， 9 ），则 2 、求由抛物线 及其在点 M （ 0 ，－ 3 ） 和 N （ 3 ， 0 ）处的两条切线所围成的图形的面积。 x y o y= － x 2 +4x-3 略解： 则在 M 、 N 点处的切线方程分别为 、 （ 3/2 ， 3 ） 3 、 在曲线 上的某点 A 处作一切线使之与曲线以及 轴所围成的面积为 . 试求：切点 A 的坐标以及切线方程 . x y O y=x 2 A B C 略解： 设切点坐标为 则切线方程为 切线与 x 轴的交点坐标为 则由题可知有 所以切点坐标与切线方程分别为 x y O y=x 2 A B C （ 1 ）画图 , 并将图形分割为若干个曲边梯形； （ 2 ）对每个曲边梯形确定其存在的范围 , 从而确定积分的上、下限； （ 3 ）确定被积函数； （ 4 ）求出各曲边梯形的面积和 , 即各积分的绝对值的和。 小结 : 求平面图形面积的方法与步骤： 以及 (1) 曲线 与直线 轴所围成的曲边梯形的面积： 以及 (2) 曲线 与直线 轴所围成的曲边梯形的面积： y a b x y a b x b 课题： 定积分的应用 我行 我能 我要成功 我能成功 几种常见的曲边梯形面积的计算方法： (3) 两条曲线 与直线 围成的曲边梯形的面积 : y a x b y a b x b 4 、求曲线 与曲线 以及 轴所围成的图形面积。 略解： 如图 由 得 当 时 则所求图形的面积为 由 得