2018-2019学年广西贵港市覃塘高级中学高二3月月考数学（文）试题 Word版 9页

‎2018-2019学年广西贵港市覃塘高级中学3月月考试题 高二文科数学 ‎ 试卷说明：本试卷分Ⅰ卷和Ⅱ卷，Ⅰ卷为试题（选择题和客观题），学生自已保存，Ⅱ卷一般为答题卷，考试结束只交Ⅱ卷。‎ 一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有 一项是符合题目要求的.‎ ‎1．在复平面内，复数的共轭复数对应的点位于（ ）‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎2．以下四个命题，其中正确的是( )‎ A．由独立性检验可知，有99%的把握认为物理成绩与数学成绩有关，某人数学成绩优秀，则他有99%的可能物理优秀；‎ B．两个随机变量相关系越强，则相关系数的绝对值越接近于0；‎ C．在线性回归方程中，当变量每增加一单位时，变量平均增加0.2个单位；‎ D．线性回归方程对应的直线至少经过其样本数据点中的一个点.‎ ‎3．有一段演绎推理：“对数函数是增函数；已知是对数函数，所以是增函数”，结论显然是错误的，这是因为（ ）‎ A．大前提错误 B．小前提错误 C．推理形式错误 D．非以上错误 ‎4．已知变量之间的线性回归方程为，且变量之间的一组关系数据如下表所示，则下列说法错误的是（ ）‎ A．变量之间呈现负相关关系 B．可以预测，当时，‎ C． D．由表格数据知，该回归直线必过点 ‎5．下列各式的运算结果为纯虚数的是 A． B． C． D．‎ ‎6．在同一平面直角坐标系中，将曲线y＝cos2x按伸缩变换后为( 　)‎ A．y′＝cos x′ B．y′＝3cosx′ C．y′＝2cosx′ D．y′＝cos 3x′‎ ‎7．利用反证法证明：“若，则”时，假设为 A．，都不为0 B．且，都不为0 C．且，不都为0 D．，不都为0‎ ‎8．在极坐标系中，极点为坐标原点，极轴为x轴正半轴，建立直角坐标系，点M（2，）的直角坐标是 A． B． C． D．‎ ‎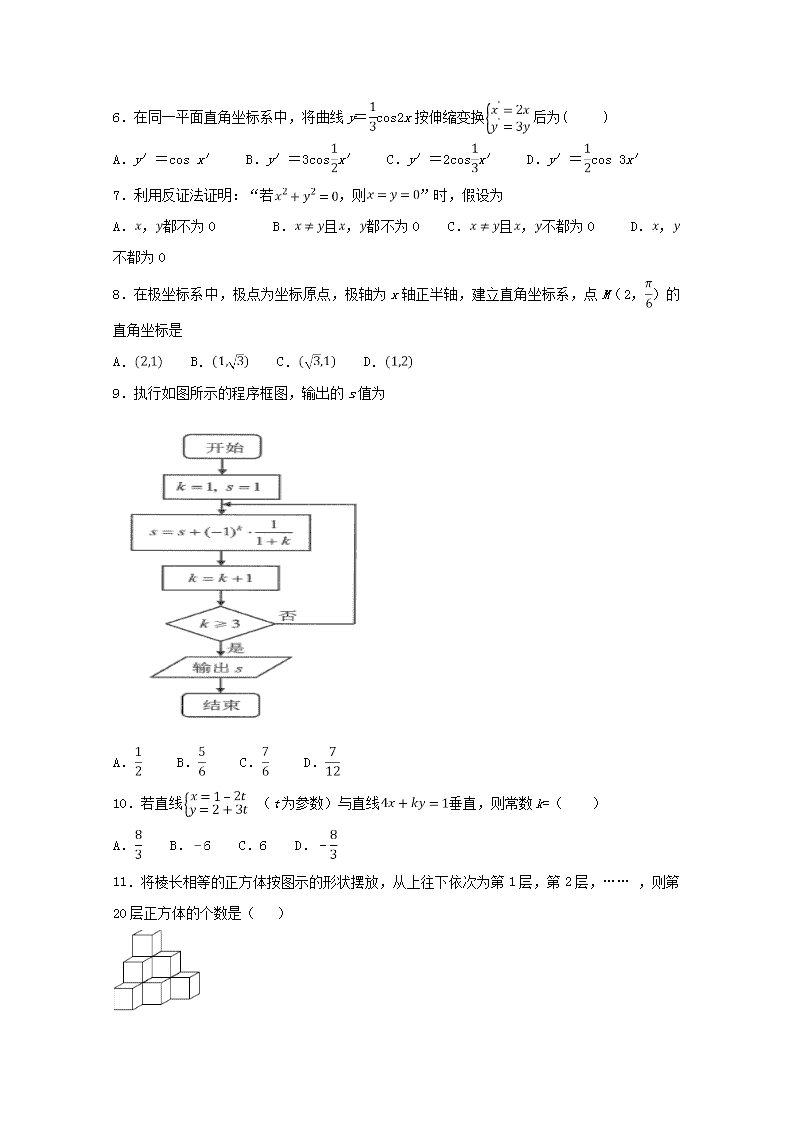9．执行如图所示的程序框图，输出的s值为 A． B． C． D．‎ ‎10．若直线 （t为参数）与直线垂直，则常数k=（　　）‎ A． B．6 C．6 D．‎ ‎11．将棱长相等的正方体按图示的形状摆放，从上往下依次为第1层，第2层，…… ，则第20层正方体的个数是（ ）‎ A．420 B．440 C．210 D．220‎ ‎12．如图是为了求出满足的最小偶数，那么在和两个空白框中，可以分别填入( )‎ A．和 B．和 C．和 D．和 二、填空题（每题5分，满分20分，将答案填在答题纸上）‎ ‎13．i是虚数单位，复数 ___________.‎ ‎14．选举时常用的选举方式是差额选举（候选人多于当选人数），某村选举村长，具体方法是：筹备选举，由乡（镇）政府提名候选人，村民投票（同意，不同意，弃权），验票统计，得票多者选为村长；若票数相等，则由乡（镇）政府决定谁当选.下面的流程图表示该选举过程，则图（1）处应填的是__________．‎ ‎15．在极坐标系中，曲线和的方程分别为和，以极点为平面直角坐标系的原点，极轴为轴正半轴，建立平面直角坐标系，则曲线和交点的直角坐标为_________.‎ ‎16．我国古代数学名著《九章算术》中割圆术有：“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣．”其体现的是一种无限与有限的转化过程，比如在 中“”即代表无限次重复，但原式却是个定值x. 这可以通过方程确定x＝2，则_______.‎ 三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） ‎ ‎17．(10分）已知复数，复数，其中是虚数单位，，为实数．‎ ‎（1）若，z1为纯虚数，求 |z1+z2| 的值；‎ ‎（2）若，求，的值．‎ ‎18．（12分）为保护农民种粮收益，促进粮食生产，确保国家粮食安全，调动广大农民粮食生产的积极性，从2004年开始，国家实施了对种粮农民直接补贴.通过对2014～2018年的数据进行调查，发现某地区发放粮食补贴额（亿元）与该地区粮食产量（万亿吨）之间存在着线性相关关系.统计数据如下表：‎ 年份 ‎2014年 ‎2015年 ‎2016年 ‎2017年 ‎2018年 补贴额亿元 ‎9‎ ‎10‎ ‎12‎ ‎11‎ ‎8‎ 粮食产量万亿吨 ‎23‎ ‎25‎ ‎30‎ ‎26‎ ‎21‎ ‎（Ⅰ）请根据如表所给的数据，求出关于的线性回归直线方程；‎ ‎（Ⅱ）通过对该地区粮食产量的分析研究，计划2019年在该地区发放粮食补贴额7亿元，请根据（Ⅰ）中所得的线性回归直线方程，预测2019年该地区的粮食产量.‎ ‎（参考公式：，）‎ ‎19．（12分）阅读下面材料：根据两角和与差的正弦公式，有 ‎ ……………①‎ ‎ ……………②‎ 由①+② 得 …………③‎ 令 有 代入③得 ．‎ ‎（1）利用上述结论，试求的值。‎ ‎（2）类比上述推证方法，根据两角和与差的余弦公式，证明: 。‎ ‎（3）求函数的最大值。‎ ‎20．（12分）在直角坐标系中，圆的方程为 ‎（Ⅰ）以坐标原点为极点，轴正半轴为极轴且具有相同单位长建立极坐标系，求的极坐标方程；‎ ‎（Ⅱ）直线的参数方程为（其中为参数），若直线与交于两点，求中点到的距离．‎ ‎21．（12分）2018年双11当天，某购物平台的销售业绩高达2135亿人民币．与此同时，相关管理部门推出了针对电商的商品和服务的评价体系，现从评价系统中选出200次成功交易，并对其评价进行统计，对商品的好评率为0.9，对服务的好评率为0.75，其中对商品和服务都做出好评的交易为140次．‎ （1） 请完成下表，并判断是否可以在犯错误概率不超过0.5％的前提下，认为商品好评与服务好评有关？‎ 对服务好评 对服务不满意 合计 对商品好评 ‎140‎ 对商品不满意 ‎10‎ 合计 ‎200‎ ‎（2）若针对服务的好评率，采用分层抽样的方式从这200次交易中取出4次交易，并从中选择两次交易进行客户回访，求只有一次好评的概率．‎ 附：，其中n＝a＋b＋c＋d．‎ P（K2≥k）‎ ‎0.15‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ k ‎2.072‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ ‎22．（12分）在平面直角坐标系xOy中，直线l的参数方程为（t为参数），以坐标原点为极点，x轴正半轴为极轴建立极坐标系，圆的极坐标方程为．‎ ‎（1）若直线l与圆相切，求的值；‎ ‎（2）若直线l与曲线（q为参数）交于A，B两点，点，求．‎ ‎2019年春季期高二文科数学3月份月考答案 一、选择题。‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 D C A C C A D C B B C D 二、填空题。‎ ‎13、‎ ‎ 14、验票系统 ‎15、 ‎ ‎16、‎ 三、解答题。‎ ‎17．(1) (2)m=0,n=-1‎ ‎【解析】（1）因为为纯虚数，所以．‎ 又，所以，，从而． ‎ 因此． ‎ ‎（2）因为，所以，‎ 即．又，为实数， ‎ 所以 解得 ‎18．（1）（2）粮食产量大约为18.7万亿吨.‎ ‎【解析】（1）由已知数据，可得，‎ ‎.‎ 代入公式，经计算，得，‎ ‎∴.‎ ‎∴所求关于的线性回归直线方程为.‎ ‎（2）由题意，知，代入（1）中所得线性回归直线方程，计算得.‎ ‎∴2019年该地区的粮食产量大约为18.7万亿吨.‎ ‎19．(1) （2）见解析（3）‎ ‎【解析】(1).‎ ‎（2）因为， ①‎ ‎ ， ② ‎ ‎①+② 得 ， ③ ‎ 令有， 代入③得：. ‎ ‎（3）.由(2)知,‎ ‎, 故函数的最大值为.‎ ‎20．（Ⅰ）；（Ⅱ）.‎ ‎【详解】（Ⅰ）由圆的方程为知：‎ 是圆的极坐标方程.‎ ‎（Ⅱ）直线的参数方程为，当时，点在直线上，故可将直线的参数方程为，代入圆：得 ，设对应的参数为.‎ ‎ 中点对应的参数为 ‎21．（1）详见解析（2）0.5‎ ‎【解析】（1）由题意可得关于商品和服务评价的2×2列联表：‎ 对服务好评 对服务不满意 合计 对商品好评 ‎140‎ ‎40‎ ‎180‎ 对商品不满意 ‎10‎ ‎10‎ ‎20‎ 合计 ‎150‎ ‎50‎ ‎200‎ 则．‎ 由于7.407＜7.879，则不可以在犯错误概率不超过0.5％的前提下，认为商品好评与服务好评有关．‎ ‎（2）若针对商品的好评率，采用分层抽样的方式从这200次交易中取出4次交易，则好评的交易次数为3次，不满意的次数为1次．‎ 记好评的交易为A，B，C，不满意的交易为a，从4次交易中，取出2次的所有取法为（A，B），（A，C），（A，a），（B，C），（B，a），（C，a），共6种情况，‎ 其中只有一次好评的情况是（A，a）、（B，a）、（C，a），共3种，‎ 因此只有一次好评的概率为．‎ ‎22．(1) (2) ‎ ‎【解析】（1）直线的普通方程为.圆的直角坐标方程为.‎ 因为直线与圆相切，所以，由于，解得.‎ ‎（2）曲线的普通方程为，点在直线上，‎ 所以直线的参数方程可以写为（为参数），‎ 将上式代入得.设A，B对应的参数分别为，‎ 所以，，所以.‎