2018-2019学年山西省晋中市平遥县第二中学高二上学期10月月考数学试题 Word版 10页

平遥二中2018-2019学年高二年级十月考试数学试题 一、选择题（本题共12小题，每小题5分，共60分）‎ ‎1、下列各组几何体中是多面体的一组是( )‎ A. 三棱柱 四棱台 球 圆锥 ‎ B. 三棱柱 四棱台 正方体 六棱锥 C. 三棱柱 四棱台 正方体 圆台 ‎ D. 圆锥 圆台 球 半球 ‎2、用符号表示“点A在直线上，在平面外”，正确的是（ ）‎ A. B. ‎ C. D．‎ ‎3、正方体的内切球和外接球的半径之比为（　 　）‎ A． B． C． D．‎ ‎4、一个正三棱柱的主视图如图所示，则其左视图的面积是( )‎ A. 1 B. 2 C. D. 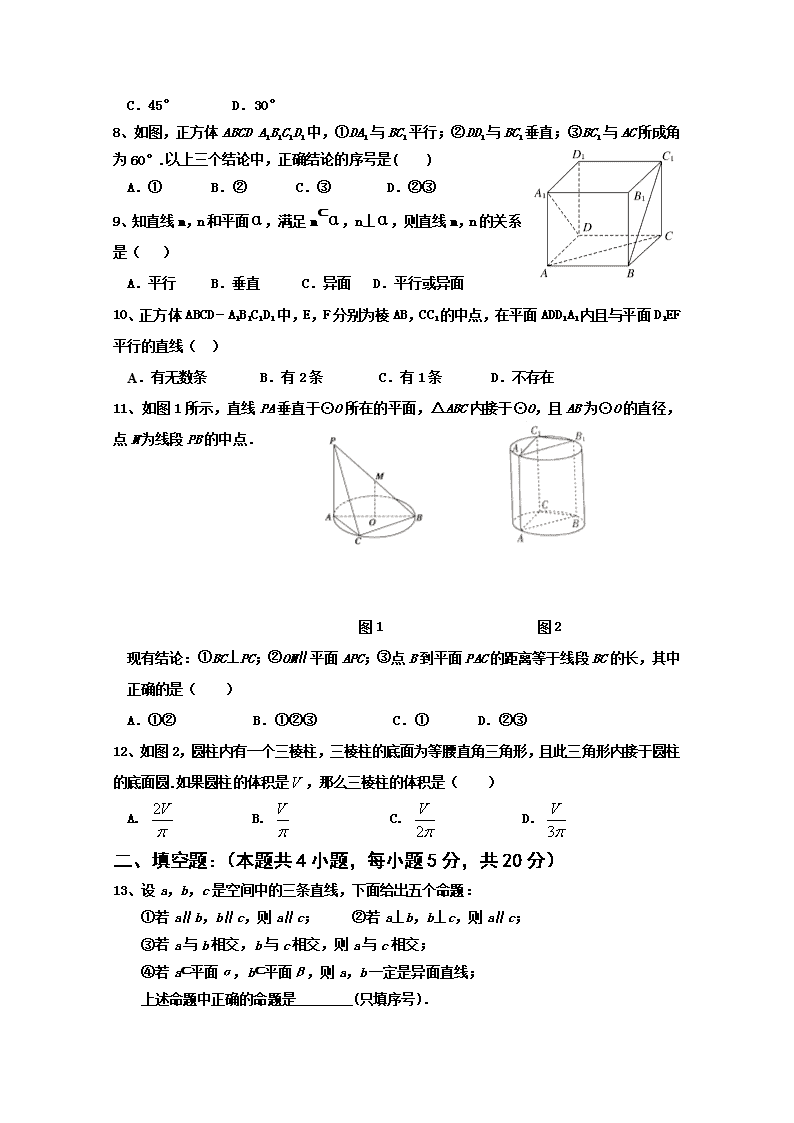‎ ‎5、如图，△O′A′B′是水平放置的△OAB的直观图，则△OAB的面积是(　　) ‎ A．6 B．3 C．6 D．12‎ ‎6、已知空间中有三条线段AB，BC和CD，且∠ABC＝∠BCD，那么直线AB与CD的位置关系是( 　)‎ A.AB∥CD B.AB与CD异面 ‎ C.AB与CD相交 D.AB∥CD或AB与CD异面或AB与CD相交 ‎7、如图，已知四棱锥的侧棱长与底面边长都是2，且SO⊥平面ABCD，O为底面的中心，则侧棱与底面所成的角为(　　)‎ A．75° B．60° ‎ C．45° D．30°‎ 8、 如图，正方体ABCDA1B1C1D1中，①DA1与BC1平行；②DD1与BC1垂直；③BC1与AC所成角为60°.以上三个结论中，正确结论的序号是(　　)‎ A．①　　 B．② C．③　　　 D．②③‎ ‎9、知直线m，n和平面α，满足m⊂α，n⊥α，则直线m，n的关系是（　 ）‎ A．平行 B．垂直 C．异面 D．平行或异面 ‎10、正方体ABCD﹣A1B1C1D1中，E，F分别为棱AB，CC1的中点，在平面ADD1A1内且与平面D1EF平行的直线（　）‎ ‎ A．有无数条 B．有2条 C．有1条 D．不存在 ‎11、如图1所示，直线PA垂直于⊙O所在的平面，△ABC内接于⊙O，且AB为⊙O的直径，点M为线段PB的中点．‎ 图1 图2‎ 现有结论：①BC⊥PC；②OM∥平面APC；③点B到平面PAC的距离等于线段BC的长，其中正确的是（ ）‎ A．①② B．①②③ C．① D．②③‎ ‎12、如图2，圆柱内有一个三棱柱，三棱柱的底面为等腰直角三角形，且此三角形内接于圆柱的底面圆.如果圆柱的体积是，那么三棱柱的体积是（ ）‎ A. B. C. D. 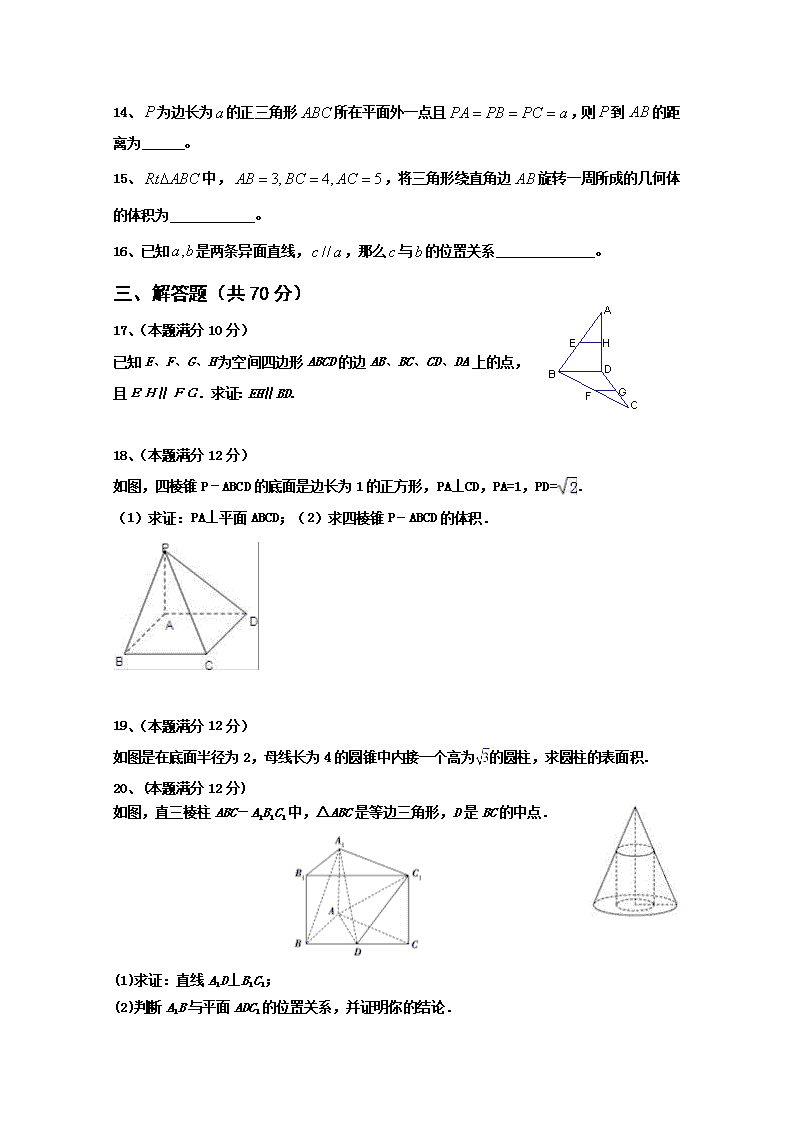‎ 二、填空题：（本题共4小题，每小题5分，共20分）‎ ‎13、设a，b，c是空间中的三条直线，下面给出五个命题：‎ ‎①若a∥b，b∥c，则a∥c； ②若a⊥b，b⊥c，则a∥c；‎ ‎③若a与b相交，b与c相交，则a与c相交；‎ ‎④若a⊂平面α，b⊂平面β，则a，b一定是异面直线；‎ 上述命题中正确的命题是________(只填序号)．‎ ‎14、为边长为的正三角形所在平面外一点且，则到的距离为______。‎ ‎15、中，，将三角形绕直角边旋转一周所成的几何体的体积为____________。 ‎ ‎16、已知是两条异面直线，，那么与的位置关系______________。‎ 三、解答题（共70分）‎ ‎17、（本题满分10分）‎ 已知E、F、G、H为空间四边形ABCD的边AB、BC、CD、DA上的点， 且ＥＨ∥ＦＧ．求证：EH∥BD. ‎ 18、 ‎（本题满分12分）‎ 如图，四棱锥P﹣ABCD的底面是边长为1的正方形，PA⊥CD，PA=1，PD=．‎ ‎（1）求证：PA⊥平面ABCD；（2）求四棱锥P﹣ABCD的体积．‎ ‎19、（本题满分12分）‎ 如图是在底面半径为2，母线长为4的圆锥中内接一个高为的圆柱，求圆柱的表面积.‎ ‎20、(本题满分12分)‎ 如图，直三棱柱ABC－A1B1C1中，△ABC是等边三角形，D是BC的中点．‎ ‎(1)求证：直线A1D⊥B1C1；‎ ‎(2)判断A1B与平面ADC1的位置关系，并证明你的结论．‎ ‎21、（本题满分12分）‎ 如图，空间四边形ABCD中，E，F分别是AB和CB上的点，G，H分别是CD和AD上的点，且EH与FG相交于点K.‎ 求证：EH，BD，FG三条直线相交于同一点。]‎ ‎22、（本题满分12分）[]‎ 如图，在三棱柱ABCA1B1C1中，AB⊥平面BB1C1C，BB1＝2BC，D，E，F分别是CC1，A1C1，B1C1的中点，G在BB1上，且BG＝3GB1.求证：‎ ‎(1)B1D⊥平面ABD； (2)平面GEF∥平面ABD.‎ 班级 姓名 考号 ‎ ‎----------------------------------------密-------------------------------封------------------------------线------------------------------------------‎ ‎ 平遥二中高二年级十月考试 ‎ 数 学 答 题 卡 一、选择题(每题5分，共60分)‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 二、填空题（每题5分，共20分）‎ ‎13、 14、 ‎ ‎15、 16、 ‎ 三、解答题 ‎17、（本题满分10分）‎ ‎18、（本题满分12分）‎ ‎19、（本题满分12分）‎ ‎20、（本题满分12分）‎ ‎21、（本题满分12分）‎ ‎[]‎ ‎22、（本题满分12分）‎ 平遥二中高二年级十月考试数学答案 一、选择题 ‎1--5 B A D C D 6--10 D C C B A 11—12 B C 二、填空题 ‎13、 ① 14、 15、 16、异面或相交 ‎ 三、解答题 ‎17、证明：面，面 面 ‎ 又面，面面， ‎ ‎18、证明：（Ⅰ）因为四棱锥P﹣ABCD的底面是边长为1的正方形， ‎ 所以PD2=PA2+AD2，所以PA⊥AD 又PA⊥CD，AD∩CD=D 所以PA⊥平面ABCD ‎（Ⅱ）解：四棱锥P﹣ABCD的底面积为1，因为PA⊥平面ABCD，所以四棱锥P﹣ABCD的高为1，所以四棱锥P﹣ABCD的体积为：．‎ ‎19、解：如图所示，设圆锥的底面半径为R，圆柱的底面半径为r，表面积为S，则R＝OC＝2，AC＝4，AO＝＝2.易知△AEB∽△AOC，‎ ‎∴＝，即＝，∴r＝1，S底＝2πr2＝2π，S侧＝2πr·h＝2π.‎ ‎∴S＝S底＋S侧＝2π＋2π＝(2＋2)π.‎ ‎20、(1)在直三棱柱ABC－A1B1C1中，AA1⊥平面ABC，所以AA1⊥BC，‎ 在等边△ABC中，D是BC中点，所以AD⊥BC，因为在平面A1AD中，A1A∩AD＝A，‎ 所以BC⊥平面A1AD，又因为A1D⊂平面A1AD，‎ 所以A1D⊥BC，‎ 在直三棱柱ABC－A1B1C1中，四边形BCC1B1是平行四边形，‎ 所以B1C1∥BC，所以，A1D⊥B1C1.‎ ‎(2)在直三棱柱ABC－A1B1C1中，四边形ACC1A1是平行四边形，在平行四边形ACC1A1中连接A1C，交AC1于点O，连接DO.‎ 故O为A1C的中点．在三角形A1CB中，D为BC中点，O为A1C中点，故DO∥A1B.‎ 因为DO⊂平面ADC1，A1B⊄平面ADC1，所以，A1B∥平面ADC1，‎ 故A1B与平面ADC1平行．‎ ‎21、证明：∵直线EH∩直线FG=K，‎ ‎∵K∈EH，EH⊂平面ABD ‎∴K∈平面ABD；‎ 同理：K∈平面BCD；‎ ‎∵平面ABD∩平面BCD=BD；‎ ‎∴K∈直线BD；‎ 即：EH、FG、BD三条直线相交于一点。‎ ‎22、证明：(1)取BB1的中点为M，连接MD，如图所示．‎ 因为BB1＝2BC，且四边形BB1C1C为平行四边形，‎ 所以四边形CDMB和四边形DMB1C1均为菱形．‎ 故∠CDB＝∠BDM，∠MDB1＝∠B1DC1，‎ 所以∠BDM＋∠MDB1＝90°，即BD⊥B1D.‎ 又AB⊥平面BB1C1C，B1D⊂平面BB1C1C，‎ 所以AB⊥B1D.‎ 又AB∩BD＝B，所以B1D⊥平面ABD.‎ ‎(2)连接MC1，可知G为MB1的中点，‎ 又F为B1C1的中点，所以GF∥MC1.‎ 又MB//C1D，‎ 所以四边形BMC1D为平行四边形，‎ 所以MC1∥BD，故GF∥BD.‎ 又BD⊂平面ABD，所以GF∥平面ABD.‎ 又EF∥A1B1，A1B1∥AB，AB⊂平面ABD，‎ 所以EF∥平面ABD.‎ 又EF∩GF＝F，故平面GEF∥平面ABD.‎