数学卷·2018届山东省德州一中高二上学期期中数学试卷（理科）+（解析版） 22页

‎2016-2017学年山东省德州一中高二（上）期中数学试卷（理科）‎ ‎　‎ 一、选择题（本大题包括12小题，每小题5分，共60分，每小题只有一个选项符合题意）‎ ‎1．直线l： x+y+3=0的倾斜角α为（　　）‎ A．30° B．60° C．120° D．150°‎ ‎2．两条不平行的直线，其平行投影不可能是（　　）‎ A．两条平行直线 B．一点和一条直线 C．两条相交直线 D．两个点 ‎3．已知圆C：x2+y2﹣2x+6y=0，则圆心P及半径r分别为（　　）‎ A．圆心P（1，3），半径r=10 B．圆心P（1，3），半径 C．圆心P（1，﹣3），半径r=10 D．圆心P（1，﹣3），半径．‎ ‎4．已知a∥α，b⊂α，则直线a与直线b的位置关系是（　　）‎ A．平行 B．相交或异面 C．异面 D．平行或异面 ‎5．过点（﹣2，4）且在两坐标轴上截距的绝对值相等的直线有（　　）‎ A．1条 B．2条 C．3条 D．4条 ‎6．在空间四边形ABCD中，E，F，G，H分别是AB，BC，CD，DA的中点．若AC=BD=a，且AC与BD所成的角为60°，则四边形EFGH的面积为（　　）‎ A． B． C． D．‎ ‎7．已知两条直线l1：x+2ay﹣1=0，l2：x﹣4y=0，且l1∥l2，则满足条件a的值为（　　）‎ A． B． C．﹣2 D．2‎ ‎8．设直线过点（0，a），其斜率为1，且与圆x2+y2=2相切，则a的值为（　　）‎ A．± B．±2 C．±2 D．±4‎ ‎9．一空间几何体的三视图如图所示，则该几何体的体积为（　　）‎ A．2π+2 B．4π+2 C．2π+ D．4π+‎ ‎10．一束光线从点（﹣1，1）出发，经x轴反射到圆C：（x﹣2）2+（y﹣3）2=1上的最短路径长度是（　　）‎ A．4 B．5 C．3 D．2‎ ‎11．点P（2，﹣1）为圆（x﹣1）2+y2=25的弦AB的中点，则直线AB的方程为（　　）‎ A．x+y﹣1=0 B．2x+y﹣3=0 C．x﹣y﹣3=0 D．2x﹣y﹣5=0‎ ‎12．四面体P﹣ABC中，若PA=PB=PC，则点P在平面ABC内的射影点O是三角形ABC的（　　）‎ A．内心 B．外心 C．垂心 D．重心 ‎　‎ 二、填空题（本题包括4个小题，每小题5分，共20分）‎ ‎13．已知⊙O1：x2+y2=1与⊙O2：（x﹣3）2+（y+4）2=9，则⊙O1与⊙O2的位置关系为　　．‎ ‎14．圆柱的侧面展开图是边长分别为2a，a的矩形，则圆柱的体积为　　．‎ ‎15．若l为一条直线，α，β，γ为三个互不重合的平面，给出下面四个命题：①α⊥γ，β⊥γ，则α⊥β；②α⊥γ，β∥γ，则α⊥β；③l∥α，l⊥β，则α⊥β．④若l∥α，则l平行于α内的所有直线．其中正确命题的序号是 　　．（把你认为正确命题的序号都填上）‎ ‎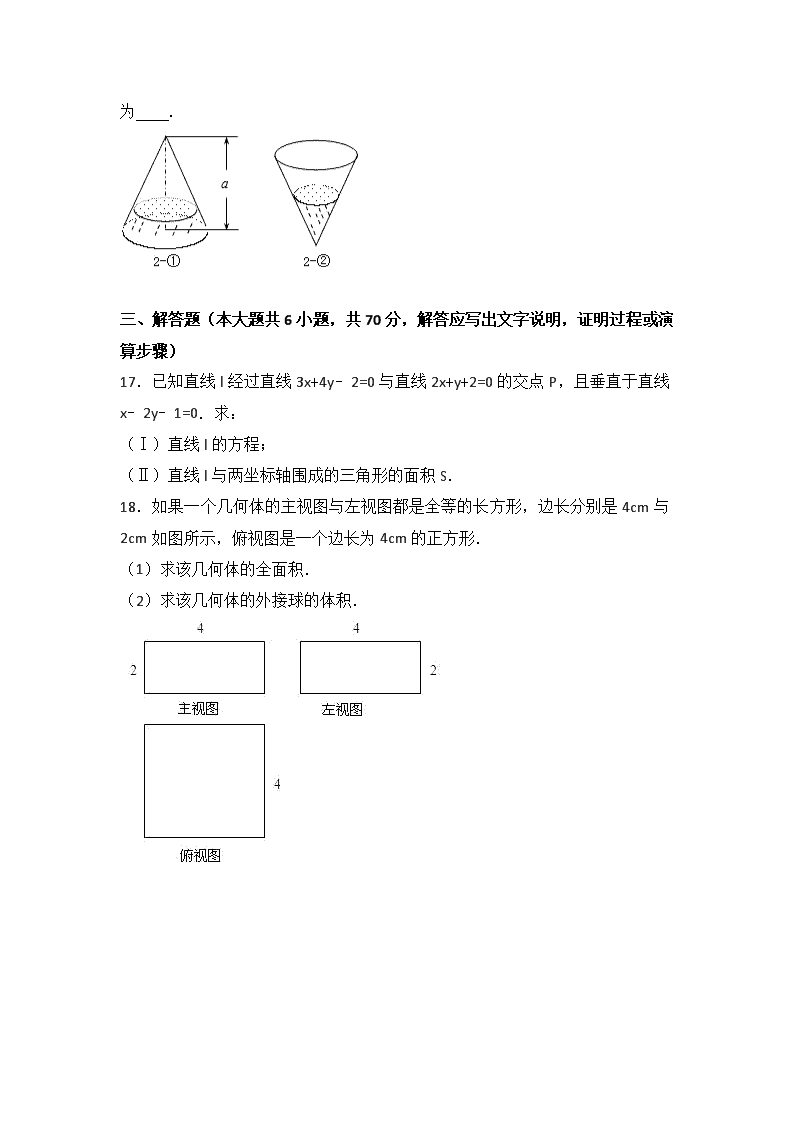16．如图2﹣①，一个圆锥形容器的高为a，内装有一定量的水．如果将容器倒置，这时所形成的圆锥的高恰为（如图2﹣②），则图2﹣①‎ 中的水面高度为　　．‎ ‎　‎ 三、解答题（本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤）‎ ‎17．已知直线l经过直线3x+4y﹣2=0与直线2x+y+2=0的交点P，且垂直于直线x﹣2y﹣1=0．求：‎ ‎（Ⅰ）直线l的方程；‎ ‎（Ⅱ）直线l与两坐标轴围成的三角形的面积S．‎ ‎18．如果一个几何体的主视图与左视图都是全等的长方形，边长分别是4cm与2cm如图所示，俯视图是一个边长为4cm的正方形．‎ ‎（1）求该几何体的全面积．‎ ‎（2）求该几何体的外接球的体积．‎ ‎19．已知直线l1：mx﹣y=0，l2：x+my﹣m﹣2=0．‎ ‎（1）求证：对m∈R，l1与l2的交点P在一个定圆上；‎ ‎（2）若l1与定圆的另一个交点为P1，l2与定圆的另一个交点为P2，求当m在实数范围内取值时，△PP1P2的面积的最大值及对应的m．‎ ‎20．已知圆C同时满足下列三个条件：①与y轴相切；②在直线y=x上截得弦长为2；③圆心在直线x﹣3y=0上．求圆C的方程．‎ ‎21．已知四棱锥P﹣ABCD，底面ABCD是∠A=60°、边长为a的菱形，又PD⊥底ABCD，且PD=CD，点M、N分别是棱AD、PC的中点．‎ ‎（1）证明：DN∥平面PMB；‎ ‎（2）证明：平面PMB⊥平面PAD；‎ ‎（3）求点A到平面PMB的距离．‎ ‎22．已知半径为5的圆的圆心在x轴上，圆心的横坐标是整数，且与直线4x+3y﹣29=0相切．‎ ‎（Ⅰ）求圆的方程；‎ ‎（Ⅱ）设直线ax﹣y+5=0（a＞0）与圆相交于A，B两点，求实数a的取值范围；‎ ‎（Ⅲ）在（Ⅱ）的条件下，是否存在实数a，使得弦AB的垂直平分线l过点P（﹣2，4），若存在，求出实数a的值；若不存在，请说明理由．‎ ‎　‎ ‎2016-2017学年山东省德州一中高二（上）期中数学试卷（理科）‎ 参考答案与试题解析 ‎　‎ 一、选择题（本大题包括12小题，每小题5分，共60分，每小题只有一个选项符合题意）‎ ‎1．直线l： x+y+3=0的倾斜角α为（　　）‎ A．30° B．60° C．120° D．150°‎ ‎【考点】直线的倾斜角．‎ ‎【分析】由题意可得，直线的斜率tanα=﹣，再由0°≤α＜180°，可得 α的值．‎ ‎【解答】解：由于直线l： x+y+3=0的倾斜角为α，则直线的斜率tanα=﹣，‎ 再由0°≤α＜180°，可得 α=120°，‎ 故选C．‎ ‎　‎ ‎2．两条不平行的直线，其平行投影不可能是（　　）‎ A．两条平行直线 B．一点和一条直线 C．两条相交直线 D．两个点 ‎【考点】平行投影及平行投影作图法．‎ ‎【分析】两条不平行的直线，要做这两条直线的平行投影，投影可能是两条平行线，可能是一点和一条直线，可能是两条相交线，不能是两个点，若想出现两个点，这两条直线需要同时与投影面垂直，这样两条线就是平行关系．‎ ‎【解答】解：∵有两条不平行的直线，‎ ‎∴这两条直线是异面或相交，‎ 其平行投影不可能是两个点，若想出现两个点，‎ 这两条直线需要同时与投影面垂直，‎ 这样两条线就是平行关系．‎ 与已知矛盾．‎ 故选D．‎ ‎　‎ ‎3．已知圆C：x2+y2﹣2x+6y=0，则圆心P及半径r分别为（　　）‎ A．圆心P（1，3），半径r=10 B．圆心P（1，3），半径 C．圆心P（1，﹣3），半径r=10 D．圆心P（1，﹣3），半径．‎ ‎【考点】圆的一般方程．‎ ‎【分析】根据已知中圆的一般方程，利用配方法，可将其化为标准方程，进而得到圆的圆心坐标及半径．‎ ‎【解答】解：圆C：x2+y2﹣2x+6y=0的方程可化为，‎ ‎（x﹣1）2+（y+3）2=10，‎ 故圆心P的坐标为（1，﹣3），半径r=‎ 故选D ‎　‎ ‎4．已知a∥α，b⊂α，则直线a与直线b的位置关系是（　　）‎ A．平行 B．相交或异面 C．异面 D．平行或异面 ‎【考点】空间中直线与直线之间的位置关系．‎ ‎【分析】由直线a∥平面α，直线b在平面α内，知a∥b，或a与b异面．‎ ‎【解答】解：∵直线a∥平面α，直线b在平面α内，‎ ‎∴a∥b，或a与b异面，‎ 故答案为：平行或异面，‎ ‎　‎ ‎5．过点（﹣2，4）且在两坐标轴上截距的绝对值相等的直线有（　　）‎ A．1条 B．2条 C．3条 D．4条 ‎【考点】直线的图象特征与倾斜角、斜率的关系．‎ ‎【分析】根据直线截距的意义即可得到结论．‎ ‎【解答】解：若直线过原点，则满足条件，此时设直线方程为y=kx，则4=﹣2k，解得k=﹣2，此时直线为y=﹣2x，‎ 若直线不经过原点，则设直线的截距式方程为，‎ ‎∵直线过点（﹣2，4，），∴，‎ ‎∵|a|=|b|，‎ ‎∴a=b或a=﹣b，‎ 若a=b，则方程等价为，解得a=b=2，此时直线方程为x+y=2，‎ 若a=﹣b，则方程等价为，解得b=6，a=﹣6，此时直线方程为x﹣y=﹣6，‎ 故满足条件的直线有3条，‎ 故选：C ‎　‎ ‎6．在空间四边形ABCD中，E，F，G，H分别是AB，BC，CD，DA的中点．若AC=BD=a，且AC与BD所成的角为60°，则四边形EFGH的面积为（　　）‎ A． B． C． D．‎ ‎【考点】异面直线及其所成的角．‎ ‎【分析】先证明四边形EFGH为菱形，然后说明∠EFG=60°，最后根据三角形的面积公式即可求出所求．‎ ‎【解答】解：连接EH，因为EH是△ABD的中位线，所以EH∥BD，且EH=BD．‎ 同理，FG∥BD，EF∥AC，且FG=BD，EF=AC．‎ 所以EH∥FG，且EH=FG．‎ 所以四边形EFGH为平行四边形．‎ 因为AC=BD=a，AC与BD所成的角为60°‎ 所以EF=EH．所以四边形EFGH为菱形，∠EFG=60°．‎ ‎∴四边形EFGH的面积是2××（）2=a2．‎ 故选A．‎ ‎　‎ ‎7．已知两条直线l1：x+2ay﹣1=0，l2：x﹣4y=0，且l1∥l2，则满足条件a的值为（　　）‎ A． B． C．﹣2 D．2‎ ‎【考点】直线的一般式方程与直线的平行关系．‎ ‎【分析】根据两直线平行，直线方程中一次项系数之比相等，但不等于常数项之比，求得a的值．‎ ‎【解答】解：根据两条直线l1：x+2ay﹣1=0，l2：x﹣4y=0，且l1∥l2，可得，求得 a=﹣2，‎ 故选C．‎ ‎　‎ ‎8．设直线过点（0，a），其斜率为1，且与圆x2+y2=2相切，则a的值为（　　）‎ A．± B．±2 C．±2 D．±4‎ ‎【考点】圆的切线方程．‎ ‎【分析】先求出过点（0，a），其斜率为1的直线方程，利用相切（圆心到直线的距离等于半径）求出a即可．‎ ‎【解答】解：设直线过点（0，a），其斜率为1，且与圆x2+y2=2相切，‎ 设直线方程为y=x+a，圆心（0，0）到直线的距离等于半径，‎ ‎∴，‎ ‎∴a的值为±2，‎ 故选B．‎ ‎　‎ ‎9．一空间几何体的三视图如图所示，则该几何体的体积为（　　）‎ A．2π+2 B．4π+2 C．2π+ D．4π+‎ ‎【考点】由三视图求面积、体积．‎ ‎【分析】由三视图及题设条件知，此几何体为一个上部是四棱锥，下部是圆柱其高已知，底面是半径为1的圆，故分别求出两个几何体的体积，再相加即得组合体的体积．‎ ‎【解答】解：此几何体为一个上部是正四棱锥，下部是圆柱 由于圆柱的底面半径为1，其高为2，故其体积为π×12×2=2π 棱锥底面是对角线为2的正方形，故其边长为，其底面积为2，又母线长为2，‎ 故其高为 由此知其体积为=‎ 故组合体的体积为2π+‎ 故选C ‎　‎ ‎10．一束光线从点（﹣1，1）出发，经x轴反射到圆C：（x﹣2）2+（y﹣3）2=1上的最短路径长度是（　　）‎ A．4 B．5 C．3 D．2‎ ‎【考点】与直线关于点、直线对称的直线方程．‎ ‎【分析】‎ 求出点A关于x轴的对称点A′，则要求的最短路径的长为A′C﹣r（圆的半径），计算求得结果．‎ ‎【解答】解：由题意可得圆心C（2，3），半径为r=1，‎ 点A关于x轴的对称点A′（﹣1，﹣1），‎ 求得A′C==5，‎ 则要求的最短路径的长为A′C﹣r=5﹣1=4，‎ 故选A．‎ ‎　‎ ‎11．点P（2，﹣1）为圆（x﹣1）2+y2=25的弦AB的中点，则直线AB的方程为（　　）‎ A．x+y﹣1=0 B．2x+y﹣3=0 C．x﹣y﹣3=0 D．2x﹣y﹣5=0‎ ‎【考点】直线与圆相交的性质．‎ ‎【分析】由垂径定理，得AB中点与圆心C的连线与AB互相垂直，由此算出AB的斜率k=1，结合直线方程的点斜式列式，即可得到直线AB的方程．‎ ‎【解答】解：∵AB是圆（x﹣1）2+y2=25的弦，圆心为C（1，0）‎ ‎∴设AB的中点是P（2，﹣1）满足AB⊥CP 因此，PQ的斜率k===1‎ 可得直线PQ的方程是y+1=x﹣2，化简得x﹣y﹣3=0‎ 故选：C ‎　‎ ‎12．四面体P﹣ABC中，若PA=PB=PC，则点P在平面ABC内的射影点O是三角形ABC的（　　）‎ A．内心 B．外心 C．垂心 D．重心 ‎【考点】棱锥的结构特征．‎ ‎【分析】由已知条件推导出△POA≌△POB≌△POC，由此能求出点P在平面ABC内的射影点O是三角形ABC的外心．‎ ‎【解答】解：设P在平面ABC射影为O，‎ ‎∵PA=PB=PC，PO=PO=PO，（公用边），∠POA=∠POB=∠POC=90°，‎ ‎∴△POA≌△POB≌△POC，‎ ‎∴OA=OB=OC，‎ ‎∴O是三角形ABC的外心．‎ 故选：B．‎ ‎　‎ 二、填空题（本题包括4个小题，每小题5分，共20分）‎ ‎13．已知⊙O1：x2+y2=1与⊙O2：（x﹣3）2+（y+4）2=9，则⊙O1与⊙O2的位置关系为　相离　．‎ ‎【考点】圆与圆的位置关系及其判定．‎ ‎【分析】先根据圆的方程得出圆的圆心坐标和半径，求出圆心距和半径之和等，再根据数量关系来判断两圆的位置关系即可．‎ ‎【解答】解：根据题意，得 ‎⊙O1的半径为r=1，⊙O2的半径为R=3，O1O2=5，‎ R+r=4，R﹣r=2，‎ 则4＜5，‎ 即R+r＜O1O2，‎ ‎∴两圆相离．‎ 故答案为：相离．‎ ‎　‎ ‎14．圆柱的侧面展开图是边长分别为2a，a的矩形，则圆柱的体积为　或　．‎ ‎【考点】棱柱、棱锥、棱台的体积．‎ ‎【分析】‎ 有两种形式的圆柱的展开图，分别求出底面半径和高，分别求出体积．‎ ‎【解答】解：圆柱的侧面展开图是边长为2a与a的矩形，‎ 当母线为a时，圆柱的底面半径是，此时圆柱体积是π×（）2×a=；‎ 当母线为2a时，圆柱的底面半径是，此时圆柱的体积是π×（）2×2a=，‎ 综上所求圆柱的体积是：或．‎ 故答案为：或；‎ ‎　‎ ‎15．若l为一条直线，α，β，γ为三个互不重合的平面，给出下面四个命题：①α⊥γ，β⊥γ，则α⊥β；②α⊥γ，β∥γ，则α⊥β；③l∥α，l⊥β，则α⊥β．④若l∥α，则l平行于α内的所有直线．其中正确命题的序号是 　②③　．（把你认为正确命题的序号都填上）‎ ‎【考点】四种命题的真假关系；空间中直线与平面之间的位置关系；平面与平面之间的位置关系．‎ ‎【分析】若α⊥γ，β⊥γ，则α与β可能平行与可能相交，可判断①的正误；‎ 由两个平行的平面与第三个平面的夹角相同，可判断②的正误；‎ 根据面面垂直的判断定理，我们判断③的正误；‎ 若l∥α，则l与α内的直线平行或异面，可判断④的正误；‎ 逐一分析后，即可得到正确的答案．‎ ‎【解答】解：①中，若α⊥γ，β⊥γ，则α与β可能平行与可能相交，故①错误；‎ ‎②中，若α⊥γ，β∥γ，则α⊥β，故②正确；‎ ‎③中，若l∥α，l⊥β，则α中存在直线a平行l，即 a⊥β，由线面垂直的判定定理，得则α⊥β，故③正确；‎ ‎④中，若l∥α，则l与α内的直线平行或异面，故④的错误；‎ 故答案：②③‎ ‎　‎ ‎16．如图2﹣①，一个圆锥形容器的高为a，内装有一定量的水．如果将容器倒置，这时所形成的圆锥的高恰为（如图2﹣②），则图2﹣①中的水面高度为　a﹣　．‎ ‎【考点】旋转体（圆柱、圆锥、圆台）．‎ ‎【分析】圆锥正置与倒置时，水的体积不变，另外水面是平行于底面的平面，此平面截得的小圆锥与原圆锥成相似体，它们的体积之比为对应高的立方比．‎ ‎【解答】解：令圆锥倒置时水的体积为V′，圆锥体积为V ‎ 则=‎ 正置后：V水=V 则突出的部分V空=V 设此时空出部分高为h，则 h3：，‎ ‎∴‎ 故水的高度为：a﹣‎ 故答案为：a﹣‎ ‎　‎ 三、解答题（本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤）‎ ‎17．已知直线l经过直线3x+4y﹣2=0与直线2x+y+2=0的交点P，且垂直于直线x﹣2y﹣1=0．求：‎ ‎（Ⅰ）直线l的方程；‎ ‎（Ⅱ）直线l与两坐标轴围成的三角形的面积S．‎ ‎【考点】直线的一般式方程；两条直线的交点坐标．‎ ‎【分析】（Ⅰ）联立两直线方程得到方程组，求出方程组的解集即可得到交点P的坐标，根据直线l与x﹣2y﹣1垂直，利用两直线垂直时斜率乘积为﹣1，可设出直线l的方程，把P代入即可得到直线l的方程；‎ ‎（Ⅱ）分别令x=0和y=0求出直线l与y轴和x轴的截距，然后根据三角形的面积函数间，即可求出直线l与两坐标轴围成的三角形的面积．‎ ‎【解答】解：（Ⅰ）由解得由于点P的坐标是（﹣2，2）．‎ 则所求直线l与x﹣2y﹣1=0垂直，可设直线l的方程为2x+y+m=0．‎ 把点P的坐标代入得2×（﹣2）+2+m=0，即m=2．‎ 所求直线l的方程为2x+y+2=0．‎ ‎（Ⅱ）由直线l的方程知它在x轴．y轴上的截距分别是﹣1．﹣2，‎ 所以直线l与两坐标轴围成三角形的面积．‎ ‎　‎ ‎18．如果一个几何体的主视图与左视图都是全等的长方形，边长分别是4cm与2cm如图所示，俯视图是一个边长为4cm的正方形．‎ ‎（1）求该几何体的全面积．‎ ‎（2）求该几何体的外接球的体积．‎ ‎【考点】由三视图求面积、体积．‎ ‎【分析】三视图复原的几何体是底面是正方形的正四棱柱，根据三视图的数据，求出几何体的表面积，求出对角线的长，就是外接球的直径，然后求它的体积即可．‎ ‎【解答】解：（1）由题意可知，该几何体是长方体，‎ 底面是正方形，边长是4，高是2，因此该 几何体的全面积是：‎ ‎2×4×4+4×4×2=64cm2‎ 几何体的全面积是64cm2．‎ ‎（2）由长方体与球的性质可得，长方体的对角线是球的直径，‎ 记长方体的对角线为d，球的半径是r，‎ d=所以球的半径r=3‎ 因此球的体积v=，‎ 所以外接球的体积是36πcm3．‎ ‎　‎ ‎19．已知直线l1：mx﹣y=0，l2：x+my﹣m﹣2=0．‎ ‎（1）求证：对m∈R，l1与l2的交点P在一个定圆上；‎ ‎（2）若l1与定圆的另一个交点为P1，l2与定圆的另一个交点为P2，求当m在实数范围内取值时，△PP1P2的面积的最大值及对应的m．‎ ‎【考点】直线与圆的位置关系；两条直线的交点坐标．‎ ‎【分析】（1）联立两条直线方程，消去m，即得到l1和l2的交点M的方程，判断对m∈R，l1与l2的交点P在一个定圆上；‎ ‎（2）由（1）得：（0，0），（2，1）．当P点在定圆上移动时，△PP1P2的底边P1P2为定值2r．当三角形的高最大时，△PP1P2的面积最大．‎ ‎【解答】解：（1）如图所示：l1：﹣y=0，过定点（0，0），=m；‎ l2：x+my﹣m﹣2=0，m（y﹣1）+x﹣2=0， =﹣‎ 令y﹣1=0，x﹣2=0．得y=1，x=2，∴过定点（2，1），‎ ‎∵•=﹣1，∴直线与直线互相垂直，‎ ‎∴直线与直线的交点必在以（0，0），（2，1）为一条直径端点的圆上，且圆心（1，），半径r==，‎ ‎∴圆的方程为（x﹣1）2+（y﹣）2=．‎ 即x2+y2﹣2x﹣y=0；‎ ‎（2）由（1）得：（0，0），（2，1）．当P点在定圆上移动时，△PP1P2的底边P1P2为定值2r．当三角形的高最大时，△PP1P2的面积最大．‎ 故三角形面积最大为•2r•r=‎ 又与圆的交点为P（，），且OP与P1P2的夹角是45°．‎ ‎∴|OP|==，即+=，解得：m=3或m=‎ 故当m=3或m=时，△PP1P2的面积取得最大值．‎ ‎　‎ ‎20．已知圆C同时满足下列三个条件：①与y轴相切；②在直线y=x上截得弦长为2；③圆心在直线x﹣3y=0上．求圆C的方程．‎ ‎【考点】圆的标准方程．‎ ‎【分析】设所求的圆C与y轴相切，又与直线y=x交于AB，由题设知圆心C（3a，a），R=3|a|，再由点到直线的距离公式和勾股定理能够求出a的值，从而得到圆C的方程．‎ ‎【解答】解设所求的圆C与y轴相切，又与直线y=x交于AB，‎ ‎∵圆心C在直线x﹣3y=0上，∴圆心C（3a，a），又圆 与y轴相切，∴R=3|a|．又圆心C到直线y﹣x=0的距离．‎ 在Rt△CBD中，，‎ ‎∴9a2﹣2a2=7．a2=1，a=±1，3a=±3．‎ ‎∴圆心的坐标C分别为（3，1）和（﹣3，﹣1），‎ 故所求圆的方程为（x﹣3）2+（y﹣1）2=9或（x+3）2+（y+1）2=9．‎ ‎　‎ ‎21．已知四棱锥P﹣ABCD，底面ABCD是∠A=60°、边长为a的菱形，又PD⊥底ABCD，且PD=CD，点M、N分别是棱AD、PC的中点．‎ ‎（1）证明：DN∥平面PMB；‎ ‎（2）证明：平面PMB⊥平面PAD；‎ ‎（3）求点A到平面PMB的距离．‎ ‎【考点】直线与平面平行的判定；平面与平面垂直的判定；点、线、面间的距离计算．‎ ‎【分析】（1）取PB中点Q，连接MQ、NQ，再加上QN∥BC∥MD，且QN=MD，于是DN∥MQ，再利用直线与平面平行的判定定理进行证明，即可解决问题；‎ ‎（2）易证PD⊥MB，又因为底面ABCD是∠A=60°、边长为a的菱形，且M为AD中点，然后利用平面与平面垂直的判定定理进行证明；‎ ‎（3）因为M是AD中点，所以点A与D到平面PMB等距离，过点D作DH⊥PM于H，由（2）平面PMB⊥平面PAD，所以DH⊥平面PMB，DH是点D到平面PMB的距离，从而求解．‎ ‎【解答】解：（1）证明：取PB中点Q，连接MQ、NQ，‎ 因为M、N分别是棱AD、PC中点，‎ 所以QN∥BC∥MD，且QN=MD，于是DN∥MQ．‎ ‎⇒DN∥平面PMB．‎ ‎（2）⇒PD⊥MB 又因为底面ABCD是∠A=60°、边长为a的菱形，且M为AD中点，‎ 所以MB⊥AD．‎ 又AD∩PD=D，‎ 所以MB⊥平面PAD. ⇒平面PMB⊥平面PAD．‎ ‎（3）因为M是AD中点，所以点A与D到平面PMB等距离．‎ 过点D作DH⊥PM于H，由（2）平面PMB⊥平面PAD，所以DH⊥平面PMB．‎ 故DH是点D到平面PMB的距离.．‎ ‎∴点A到平面PMB的距离为．‎ ‎　‎ ‎22．已知半径为5的圆的圆心在x轴上，圆心的横坐标是整数，且与直线4x+3y﹣29=0相切．‎ ‎（Ⅰ）求圆的方程；‎ ‎（Ⅱ）设直线ax﹣y+5=0（a＞0）与圆相交于A，B两点，求实数a的取值范围；‎ ‎（Ⅲ）在（Ⅱ）的条件下，是否存在实数a，使得弦AB的垂直平分线l过点P（﹣2，4），若存在，求出实数a的值；若不存在，请说明理由．‎ ‎【考点】直线和圆的方程的应用；圆的标准方程．‎ ‎【分析】（Ⅰ）设圆心为M（m，0）（m∈Z）．由于圆与直线4x+3y﹣29=0相切，且半径为5，所以，由此能求了圆的方程．‎ ‎（Ⅱ）把直线ax﹣y+5=0代入圆的方程，得（a2+1）x2+2（5a﹣1）x+1=0，由于直线ax﹣y+5=0交圆于A，B两点，故△=4（5a﹣1）2﹣4（a2+1）＞‎ ‎0，由此能求出实数a的取值范围．‎ ‎（Ⅲ）设符合条件的实数a存在，则直线l的斜率为，l的方程为，由于l垂直平分弦AB，故圆心M（1，0）必在l上，由此推导出存在实数使得过点P（﹣2，4）的直线l垂直平分弦AB．‎ ‎【解答】（本小题满分14分）‎ 解：（Ⅰ）设圆心为M（m，0）（m∈Z）．‎ 由于圆与直线4x+3y﹣29=0相切，且半径为5，‎ 所以，‎ 即|4m﹣29|=25．因为m为整数，故m=1．‎ 故所求圆的方程为（x﹣1）2+y2=25． …‎ ‎（Ⅱ）把直线ax﹣y+5=0，即y=ax+5，‎ 代入圆的方程，消去y，‎ 整理，得（a2+1）x2+2（5a﹣1）x+1=0，‎ 由于直线ax﹣y+5=0交圆于A，B两点，‎ 故△=4（5a﹣1）2﹣4（a2+1）＞0，‎ 即12a2﹣5a＞0，‎ 由于a＞0，解得a＞，‎ 所以实数a的取值范围是（）．‎ ‎（Ⅲ）设符合条件的实数a存在，‎ 则直线l的斜率为，‎ l的方程为，‎ 即x+ay+2﹣4a=0‎ 由于l垂直平分弦AB，故圆心M（1，0）必在l上，‎ 所以1+0+2﹣4a=0，解得．‎ 由于，故存在实数 使得过点P（﹣2，4）的直线l垂直平分弦AB．…‎ ‎　‎