2020届二轮复习平面向量数量积的物理背景及其含义课件（10张）（全国通用） 10页

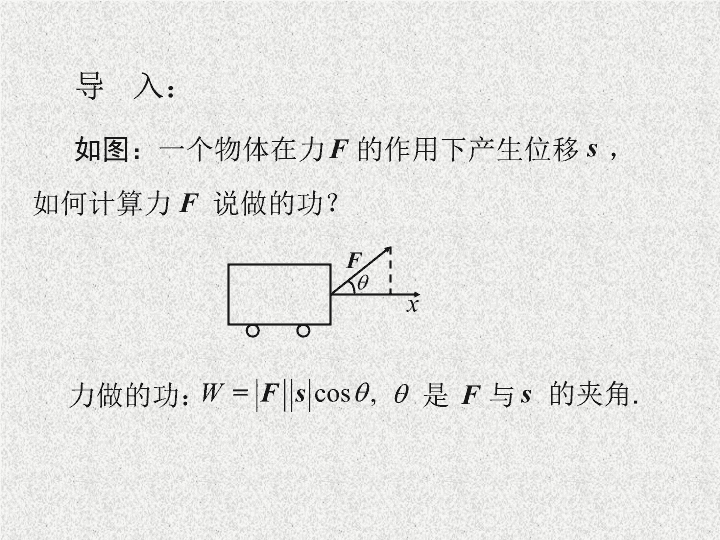
如图： 一个物体在力 的作用下产生位移 ， 如何计算力 说做的功？ 力做的功： 是 与 的夹角 . 导 入： 向量的数量积（或内积）定义 叫做向量 和 的数量积（或内积）， 记作 ，即 其中 是 与 的夹角 . 注意 : 两个向量的数量积是一个实数，可以是正数，负数，零 . 投影： 零向量与任一向量的数量积为 0 . 思考： 2. 投影的正负与什么有关？ 1. 投影是一个数量还是一个向量？ 向量的数量积的几何意义 由投影的意义，我们可以得到 的几何 意义：数量积 等于 的长度 与 在 的方向上的投影 的乘积 . 两个向量数量积的性质 数量积的运算律： 例 2 ：求证： 证明：