- 479.50 KB
- 2021-06-10 发布
- 1、本文档由用户上传，淘文库整理发布，可阅读全部内容。
- 2、本文档内容版权归属内容提供方，所产生的收益全部归内容提供方所有。如果您对本文有版权争议，请立即联系网站客服。
- 3、本文档由用户上传，本站不保证质量和数量令人满意，可能有诸多瑕疵，付费之前，请仔细阅读内容确认后进行付费下载。
- 网站客服QQ：403074932
2.4
正态分布
(
二
)
高二数学 选修
2-3
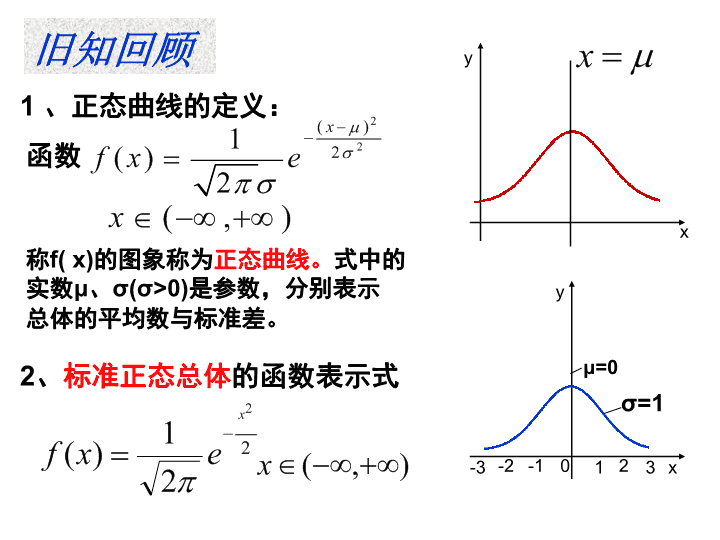
旧知回顾
函数
称
f( x)
的图象称为
正态曲线。
式中的
实数
μ
、
σ(σ>0)
是参数，分别表示
总体的平均数与标准差。
1
、正态曲线的定义：
x
y
2
、
标准正态总体
的函数表示式
0
1
2
-1
-2
x
y
-3
3
μ=0
σ=1
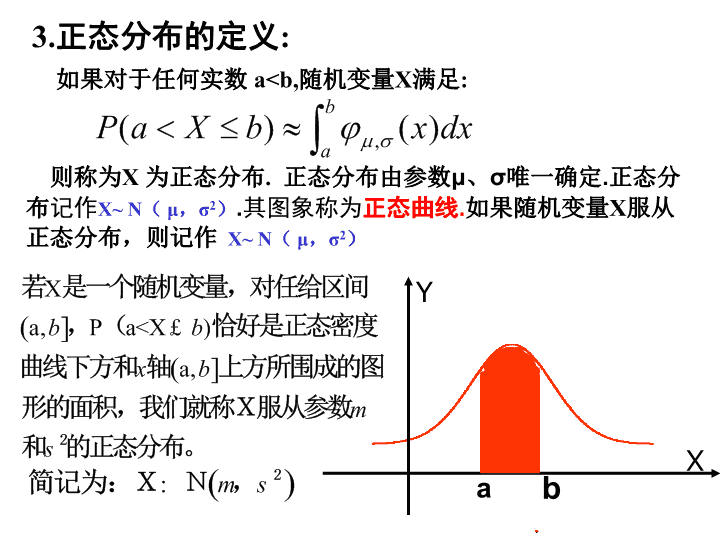
3.
正态分布的定义
:
如果对于任何实数
a0,
概率
为如图中的阴影部分的面积，对于固定的 和 而言，该面积随着 的减少而变大。这说明 越小
,
落在区间 的概率越大，即
X
集中在 周围概率越大。
特别地有
我们从上图看到，正态总体在 以外取值的概率只有
4.6
％，在 以外取值的概率只有
0.3
％。
由于这些概率值很小（一般不超过
5
％ ），通常称这些情况发生为
小概率事件
。
区 间
取值概率
（
μ
－
σ
，
μ
＋
σ]
68.3%
（
μ
－
2σ
，
μ
＋
2σ]
95.4%
（
μ
－
3σ
，
μ
＋
3σ]
99.7%
例
1
、在某次数学考试中，考生的成绩 服从一个正态分布，即
~N(90,100).
（
1
）试求考试成绩 位于区间
(70,110)
上的概率是多少？
（
2
）若这次考试共有
2000
名考生，试估计考试成绩在
(80,100)
间的考生大约有多少人？
练习：
1
、已知一次考试共有
60
名同学参加，考生的成绩
X~
，据此估计，大约应有
57
人的分数在下列哪个区间内？（ ）
(90,110] B. (95,125] C. (100,120] D.(105,115]
C
2
、已知
X~N (0,1)
，则
X
在区间 内取值的概率等于（ ）
A.0.9544 B.0.0456 C.0.9772 D.0.0228
3
、设离散型随机变量
X~N(0,1),
则
=
,
=
.
D
0.5
0.9544
4
、若已知正态总体落在区间 的概率为
0.5
，则相应的正态曲线在
x=
时达到最高点。
0.3
5
、已知正态总体的数据落在（
-3,-1
）里的概率和落在（
3,5
）里的概率相等，那么这个正态总体的数学期望是
。
1
例
3
、若
X~N(5,1),
求
P(6
微信/支付宝扫码支付下载-
关注微信公众号售出明细实时看