数学文卷·2019届山西省运城市康杰中学高二上学期第一次月考（2017-09） 9页

康杰中学2017—2018学年度第一学期月考 高二数学（文）试题 ‎2017.9‎ 一、选择题：（本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，选择一个符合题目要求的选项.）‎ ‎1. 下列各组几何体中是多面体的一组是 ‎ A. 三棱柱 四棱台 球 圆锥 ‎ B. 三棱柱 四棱台 正方体 圆台 ‎ C. 三棱柱 四棱台 正方体 六棱锥 ‎ D. 圆锥 圆台 球 半球 ‎2．正方体的内切球和外接球的半径之比为 ‎ A． B． C． D.‎ ‎3. 若一个三角形，采用斜二测画法作出其直观图，其直观图面积是原三角形面积的 A. 倍 B. 倍 C. 2倍 D.倍 ‎4. 一个四面体的所有棱长为，四个顶点在同一球面上，则此球的表面积为 A. 　　　　 B. 　　　　 C. 　　　 D. ‎ ‎5. 空间四边形SABC中，各边 及对角线长都相等，若E、F 分别为SC、AB的中点，那么异面直线EF与SA所成的角为 A. 300 B. 450 C. 600 D. 900‎ ‎6．设是两条不同的直线，是三个不同的平面，给出下列四个命题：‎ ‎ ①若，，则 ②若，，，则 ‎ ③若，，则 ④若，，则 ‎ 其中正确命题的序号是 ‎ ‎ A. ①和② B. ②和③ C. ③和④ D. 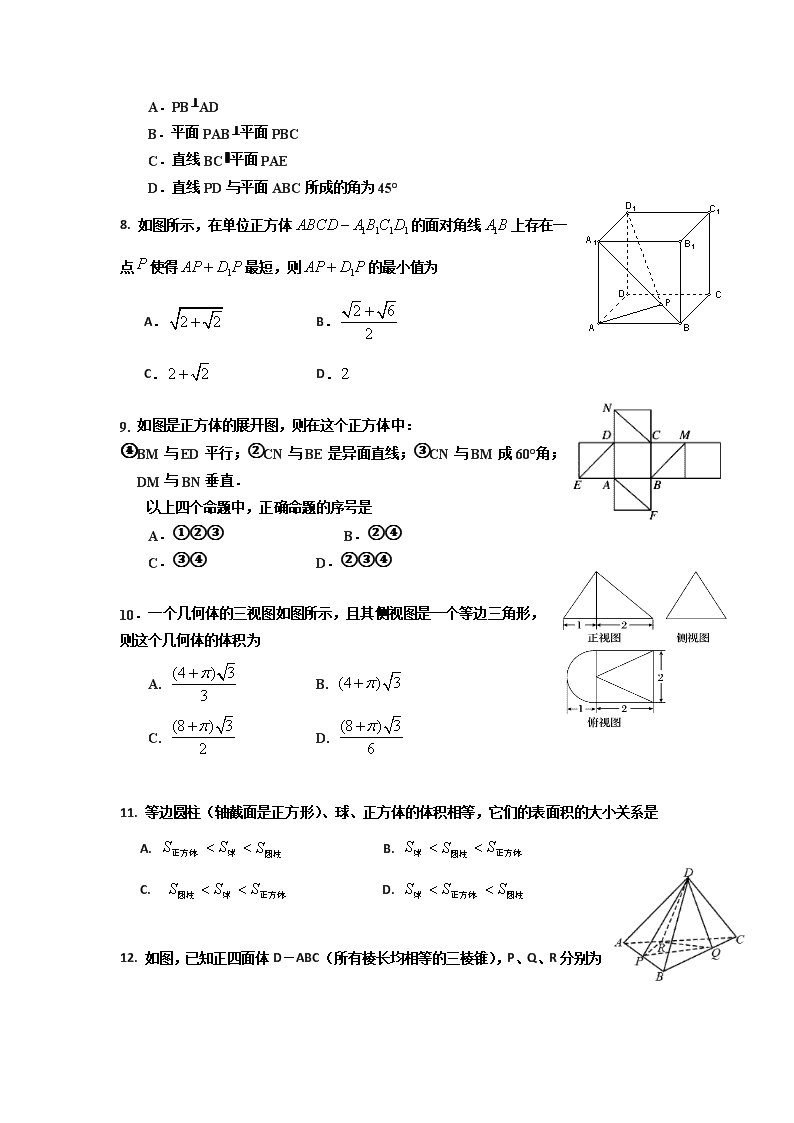①和④‎ ‎7. 如图，已知六棱锥P－ABCDEF的底面是正六边形，PA⊥平面ABC，PA＝2AB，则下列结论正确的是 A．PB⊥AD B．平面PAB⊥平面PBC C．直线BC∥平面PAE D．直线PD与平面ABC所成的角为45°‎ ‎8. 如图所示，在单位正方体的面对角线上存在一点使得最短，则的最小值为 A． B． ‎ C． D． ‎ ‎9. 如图是正方体的展开图，则在这个正方体中：‎ ‎①BM与ED平行；②CN与BE是异面直线；③CN与BM成60°角；④DM与BN垂直．‎ 以上四个命题中，正确命题的序号是 A．①②③ B．②④‎ C．③④ D．②③④‎ ‎10．一个几何体的三视图如图所示，且其侧视图是一个等边三角形，则这个几何体的体积为 A. B. ‎ C. D. ‎ ‎11. 等边圆柱（轴截面是正方形）、球、正方体的体积相等，它们的表面积的大小关系是 A. 　 B. ‎ C. D. ‎ ‎12.‎ ‎ 如图，已知正四面体D－ABC（所有棱长均相等的三棱锥），P、Q、R分别为AB，BC，CA上的点，AP＝PB，，分别记二面角D－PR－Q，D－PQ－R，D－QR－P的平面角为，则 A. B. C. D. ‎ 二、填空题（本大题共4小题，每小题5分，共20分）。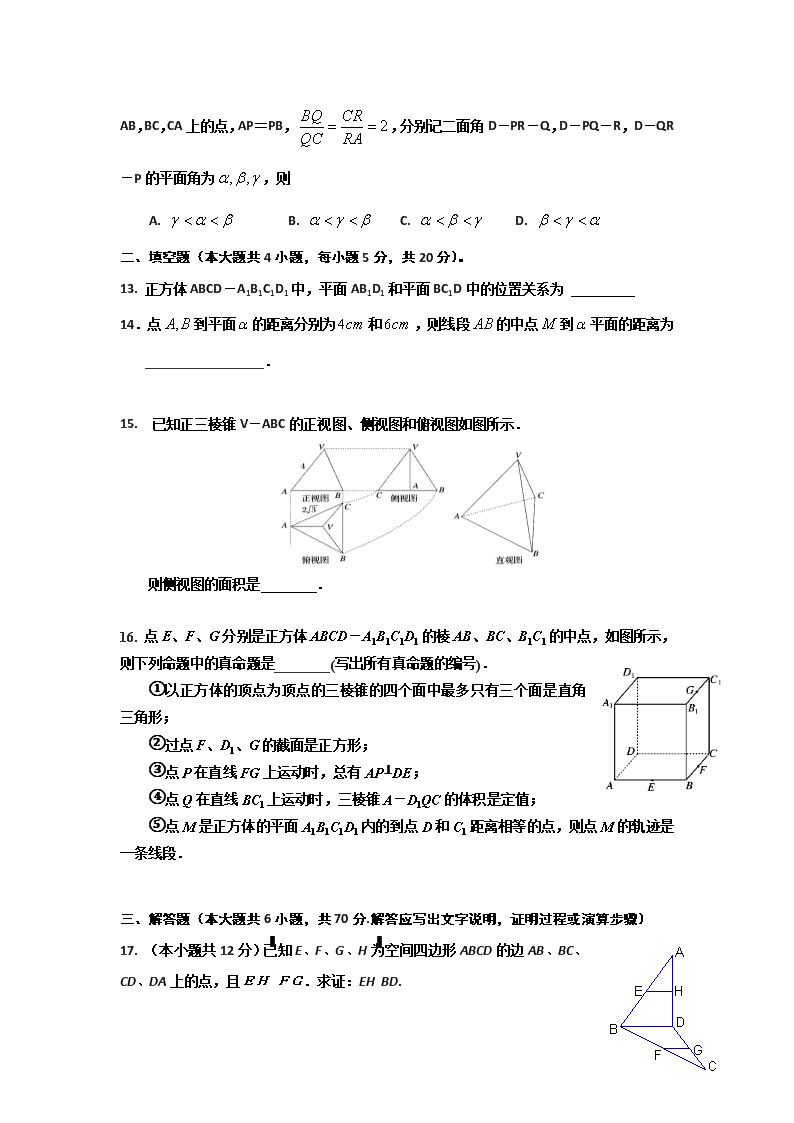‎ ‎13. 正方体ABCD－A1B1C1D1中，平面AB1D1和平面BC1D中的位置关系为 ‎ ‎14．点到平面的距离分别为和，则线段的中点到平面的距离为_________________．‎ ‎15. 已知正三棱锥V－ABC的正视图、侧视图和俯视图如图所示．‎ 则侧视图的面积是 ．‎ ‎16. 点E、F、G分别是正方体ABCD－A1B1C1D1的棱AB、BC、B1C1的中点，如图所示，则下列命题中的真命题是________(写出所有真命题的编号)．‎ ‎①以正方体的顶点为顶点的三棱锥的四个面中最多只有三个面是直角三角形；‎ ‎②过点F、D1、G的截面是正方形；‎ ‎③点P在直线FG上运动时，总有AP⊥DE；‎ ‎④点Q在直线BC1上运动时，三棱锥A－D1QC的体积是定值；‎ ‎⑤点M是正方体的平面A1B1C1D1内的到点D和C1距离相等的点，则点M的轨迹是一条线段．‎ 三、解答题（本大题共6小题，共70分.解答应写出文字说明，证明过程或演算步骤）‎ ‎17. （本小题共12分）已知E、F、G、H为空间四边形ABCD的边AB、BC、CD、DA上的点， 且ＥＨ∥ＦＧ．求证：EH∥BD. ‎ ‎18. （本小题12分）如图，在三棱锥P–ABC中，PA⊥AB，PA⊥BC，AB⊥BC，PA=AB=BC=2，D为线段AC的中点，E为线段PC上一点．‎ ‎（1）求证：PA⊥BD；‎ ‎（2）求证：平面BDE⊥平面PAC；‎ ‎（3）当PA∥平面BDE时，求三棱锥E–BCD的体积．‎ ‎19. 如图，四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，点E在线段AD上， 且CE∥AB.‎ ‎（1）求证：CE⊥平面PAD；‎ ‎（2）若PA=AB=1，AD=3，CD=，∠CDA=45°，‎ 求四棱锥P-ABCD的体积 ‎20.（本小题满分12分）在直三棱柱ABC－A1B1C1中，AB1⊥BC1，AB=CC1=1，BC=2.‎ ‎（1）求证：A1C1⊥AB；‎ ‎（2）求点B1到平面ABC1的距离.‎ ‎21.（本小题满分12分） 已知正四棱锥的底面边长和侧棱长均为，、分别是、上的点，且.‎ ‎（1）求证：直线∥平面；‎ ‎（2）求直线与平面所成的角的正切值；‎ ‎22.（本小题满分14分）已知△BCD中，∠BCD=90°，BC=CD=1，AB⊥平面BCD，∠ADB=60°，E、F分别是AC、AD上的动点，且.‎ ‎（1）求证：不论λ为何值，总有平面BEF⊥平面ABC；‎ ‎（2）当λ为何值时，平面BEF⊥平面ACD？ (14分)‎ 高二数学（文）答案 ‎1－5　CDBAB 6－10　ADACD 11－12　BB ‎13．平行 14.　1cm或5cm 15.　6　　　　　　16.　③④⑤‎ ‎17. 证明：面，面 面 ……………………6分 ‎ 又面，面面，‎ ‎ …………………………12分 ‎18.（1）因为PAAB，PABC，所以PA平面ABC，又因为BD平面ABC，‎ 所以PABD.‎ ‎（2）因为AB＝BC，D为AC中点，所以BDAC，‎ 由（1）知，PABD，所以BD平面PAC，‎ 所以平面BDE平面PAC.‎ ‎（3）因为PA//平面BDE，平面PAC平面BDE＝DE，所以PA//DE.‎ 因为D为AC的中点，所以DE＝PA＝1，BD＝DC＝.‎ 由（1）知，PA平面ABC，所以DE平面ABC.‎ 所以三棱锥E－BCD的体积V＝.‎ ‎19. 证明：（1）　　‎ 又平面ABCD，CE平面ABCD CEPA 又　平面PAD，平面PAD ‎（2）在四边形ABCD中，‎ ED＝EC＝1　　BC//AD　BC＝2‎ ‎　S四边形ABCD=　　‎ ‎20. 证明：（1）连结，则 又∵∴平面 ‎ ‎∴ ………4分 又∵ ∴平面 ‎∴ …………………4分 ‎（2）由（1）知 ∵‎ ‎ ∵ ‎ ‎∴ ‎ ‎∴ …………………6分 ‎ 设所求距离为 ‎∵∴‎ ‎∴ ∴ …………10分 ‎21.证明：（1）连结并延长与交于 ‎∵∽ ∴‎ ‎∴　∴∥………………5分 又∵平面 ‎∴∥平面……………6分 ‎（2）∵∥‎ ‎∴、与平面所成的角相等…………………8分 设、交于，连结、‎ ‎∵，∴为所求的角……………9分 ‎∵ ∴‎ 在中 ‎ ‎……10分 ‎ 又∵ ∴‎ 在中 …………………12分 ‎22.　证明：（Ⅰ）∵AB⊥平面BCD， ∴AB⊥CD，‎ ‎ ∵CD⊥BC且AB∩BC=B， ∴CD⊥平面ABC. …………3分 ‎ 又 ‎ ∴不论λ为何值，恒有EF∥CD，∴EF⊥平面ABC，EF平面BEF,‎ ‎ ∴不论λ为何值恒有平面BEF⊥平面ABC. …………6分 ‎（Ⅱ）由（Ⅰ）知，BE⊥EF，又平面BEF⊥平面ACD，‎ ‎∴BE⊥平面ACD，∴BE⊥AC. …………………………9分 ‎∵BC=CD=1，∠BCD=90°，∠ADB=60°，‎ ‎∴ …………………………11分 由AB2=AE·AC 得…………13分 ‎ 故当时，平面BEF⊥平面ACD. ………………14分