云南师范大学实验中学2020届高三毕业生复习统一检测数学（文）试题 14页

云南师范大学实验中学2020届高三毕业生复习统一检测文科数学试题卷 考试用时120 分钟，满分150分.‎ 第I卷(选择题共60分)‎ 一、选择题(本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项符合题目要求)‎ ‎1. 设集合A={1,3,5,7},B={x|2≤x≤5}, 则A∩B= ( )‎ A. {3,5} B. (3,5) C. {3,4,5} D. [3,5]‎ ‎2.设则|z|= ( )‎ A.0 B.1 D.3‎ ‎3.下图为某地区2007年~ 2019年地方财政预算内收入、城乡居民储蓄年末余额折线图.‎ 根据该折线图，下列结论正确的是()‎ A.财政预算内收入、城乡居民储蓄年末余额均呈增长趋势 B.财政预算内收入、城乡居民储蓄年末余额的逐年增长速度相同 C.财政预算内收入年平均增长量高于城乡居民储蓄年末余额年平均增长量 D.城乡居民储蓄年末余额与财政预算内收入的差额逐年增大 ‎4.若变量x,y满足约束条件则目标函数z=x-2y的最小值为( )‎ A.1 B.‎-2 ‎ C.-5 D. -7‎ ‎5.设,则f[f(11)]的值是()‎ A.1 B. 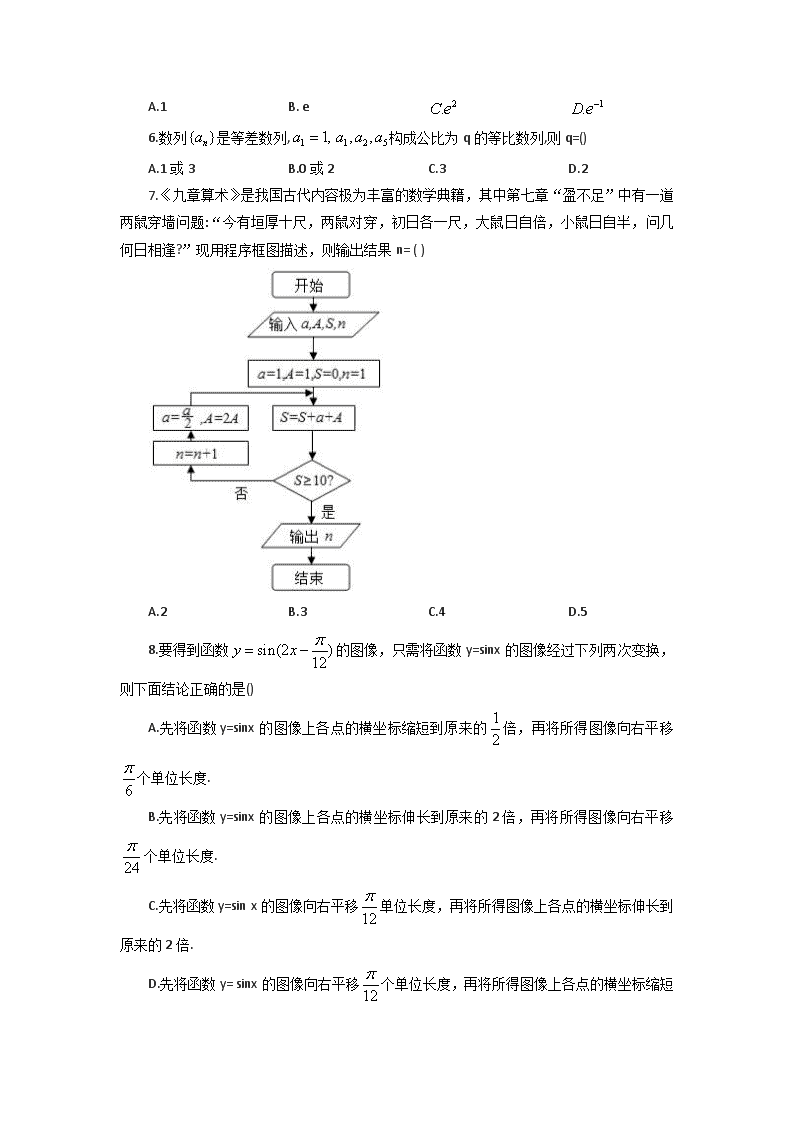e ‎ ‎6.数列是等差数列,构成公比为q的等比数列,则q=()‎ A.1或3 B.0或‎2 ‎ C.3 D.2‎ ‎7.《九章算术》是我国古代内容极为丰富的数学典籍，其中第七章“盈不足”中有一道两鼠穿墙问题:“今有垣厚十尺，两鼠对穿，初日各一尺，大鼠日自倍，小鼠日自半，问几何日相逢?”现用程序框图描述，则输出结果n= ( )‎ A.2 B‎.3 ‎ C.4 D.5‎ ‎8.要得到函数的图像，只需将函数y=sinx的图像经过下列两次变换，则下面结论正确的是()‎ A.先将函数y=sinx的图像上各点的横坐标缩短到原来的倍，再将所得图像向右平移个单位长度.‎ B.先将函数y=sinx的图像上各点的横坐标伸长到原来的2倍，再将所得图像向右平移个单位长度.‎ C.先将函数y=sin x的图像向右平移单位长度，再将所得图像上各点的横坐标伸长到原来的2倍.‎ D.先将函数y= sinx的图像向右平移 个单位长度，再将所得图像上各点的横坐标缩短到原来的倍.‎ ‎9.已知双曲线的右焦点为F,第一象限内的点A在双曲线C的渐近线上，O为坐标原点，若∠AOF=∠OAF,则△OAF的面积为( )‎ A.1 D.2‎ ‎10.在棱长为2的正方体中，点M是棱AD上一动点,则下列选项中不正确的是()‎ A.异面直线与所成的角的大小为 ‎ B.直线与平面一定平行 C.三棱锥的体积为定值4 ‎ ‎11.函数满足f(x+1)=f(1-x),且f(0)=3,则与的大小关系是()‎ A.与x有关,不确定 B . ‎ C . D . ‎ ‎12.已知是椭圆和双曲线的公共焦点, P是它们的一个公共点,且记椭圆和双曲线的离心率分别为，则的最大值为( )‎ ‎ D.1‎ 第II卷(非选择题共90分)‎ 二、填空题(本大题共4小题，每小题5分，共20分)‎ ‎13.某学校美术室收藏有4幅国画，分别为山水、花鸟各2幅，现从中随机抽取2幅进行展览，则恰好抽到2幅不同种类的概率为___.‎ ‎14.设向量且(则λ=___.‎ ‎15.已知圆柱的高为侧面积为它的两个底面的圆周在球心为O，半径为R的同一个球的球面上，则该球O的表面积为____.‎ ‎16.已知数列的前n项和为数列的前n项和为满足且若对恒成立，则实数λ 的最小值为___.‎ 三、解答题(本题共6小题，共70分.解答应写出文字说明，证明过程或演算步骤)‎ ‎17. (本小题满分12分)‎ 某微商对某种产品每天的销售量(x件)进行为期一个月的数据统计分析,并得出了该月销售量的直方图(一个月按30天计算)如图所示.假设用直方图中所得的频率来估计相应的事件发生的概率.‎ ‎(I)求频率分布直方图中的a的值;‎ ‎(II)求日销量的平均值(同一-组中的数据用该组区间的中点值作代表) ;‎ ‎(III)若微商在一天的销售量不低于25件,则上级商企会给微商赠送100元的礼金,估计该微商在一年内获得的礼金数.‎ ‎18.(本小题满分12分)‎ 如图，在四棱锥P-ABCD中，PD⊥平面ABCD，，AB//DC，∠BCD= 90°‎ ‎(I)求证:PC⊥BC ;‎ ‎(II)求点A到平面PBC的距离.‎ ‎19. (本小题满分12分)‎ 在锐角三角形ABC中,角A, B,C所对的边分别为a,b,c,若.‎ ‎(I)求角A的大小;‎ ‎(II)若2b，求△ABC面积的最大值.‎ ‎20. (本小题满分12分)‎ 已知M是抛物线上一点，F是抛物线C的焦点, |MF|=4.‎ ‎(I)求直线MF的斜率;‎ ‎(II) 已知动圆E的圆心E在抛物线C上，点D(2,0)在圆E上，且圆E与y轴交于A,B两点,令|DA|=m,|DB|=n,求的最大值.‎ ‎21.(本小题满分12分)‎ 已知函数 ‎(I)若函数f(x)在(1, f(1))处的切线与直线x-y=0平行,求实数a的值;‎ ‎(II)当a=2, k为整数, 且当x>1时，求k的最大值.‎ 选考题:‎ 请考生在第22、23两道题中任选一题作答.如果多做，则按所做的第一题计分.‎ ‎22. (本小题满分10分) [选修4-4:坐标系与参数方程]‎ 在直角坐标系xOy中，曲线C的参数方程为(α为参数),以坐标原点为极点，x轴的非负半轴为极轴建立极坐标系.‎ ‎(I)求曲线C的极坐标方程;‎ ‎(II) 设A,B为曲线C上两点(均不与O重合)，且满足求|OA|+|OB|的最大值.‎ ‎23. (本小题满分10分) [选修4-5:不等式选讲]‎ 已知函数f(x)=|x+1|+|x-1|‎ ‎(I)求不等式f(x)≤8的解集M ;‎ ‎(II)若m为M中的最大元素，正数a,b满足证明 ‎2020届高三毕业生复习统一检测 文科数学答案 一、 选择题 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ A B D C B A C D D C D B 二、 填空题 ‎13、 14、 3 15、 16、‎ 1. 集合，，故选A.‎ 2. ‎，则，故选B.‎ ‎3. 由图知，财政预算内收入08、09、10没有明显变化,故A错，B、C明显也错，故选D.‎ ‎ ‎ ‎4.由图知，z=x-2y在点处取得最小值-5.故选C.‎ ‎5.，，故选B.‎ ‎6.解析：设等差数列的公差为，构成公比为q的等比数列， 解得，于是q=1或3，故选择A.‎ ‎7.模拟执行程序，可得，，，，;‎ 不满足条件，执行循环体，，，，;‎ 不满足条件，执行循环体，，，，;‎ 不满足条件，执行循环体，，，，;‎ 满足条件，退出循环，输出的值为4．‎ 故选：C.‎ ‎8.先将的图像上各点的横坐标缩短到原来的倍，得到函数的图像，再将所得图像向右平移个单位长度，可得函数的图像；先将的图像向右平移个单位长度，得到函数的图像，再将所得图像上各点的横坐标缩短到原来的倍，可得函数的图像.故选D.‎ ‎9.如图，过作于点D，所以，因为，所以，‎ ‎,故选D.‎ ‎10.因为，所以为异面直线与所成的角，为等边三角形，所以，得异面直线与所成的角的大小为，A正确；平面平面，平面，所以平面，B正确；，C错误;正方体中，平面，平面，所以，D正确,故选C.‎ ‎11.由得，对称轴为，即，，，当时，，在上单调递减，所以；当时，，所以；当时，，在 上单调递增，所以；综上.故选D.‎ 12. 不妨设椭圆的方程为，双曲线方程为，点在第一象限，由椭圆和双曲线的定义得：，解得在中，由余弦定理得：，，当且仅当时，等号成立.‎ 所以的最大值为，所以选择B.‎ ‎13..‎ ‎14.，，解得.‎ ‎15.设圆柱的底面圆的半径为，由圆柱的侧面积为解得外接球的半径，球的表面积为.‎ ‎16.解析：当时，，解得.当时,由得.依据叠乘法（累乘法）可得.由得，‎ 于是.‎ 由于对恒成立，，故实数的最小值为.‎ 一、 解答题 ‎17 【解析】（I）由题意可得 ‎；……………4分 ‎（II）根据已知的频率分布直方图,日销售量的平均值为；……………8分 ‎（III）根据频率分布直方图,日销售量不低于25件的天数为,可获得的奖励为900元, 依次可以估计一年内获得的礼金数为元.……………12分 ‎18.【解析】（I）‎ ‎…………………2分 ‎ ……………………4分 ‎……………………………………6分 ‎（II）设点A到平面PBC的距离为h ‎，PD为三棱锥的高，………………8分 由，‎ 得，…………………………10分 即，解得，‎ 所以点A到平面PBC的距离为2. ……………………………12分 ‎19.【解析】（I）由及正弦定理得：，……………………2分 ‎，，所以，‎ ‎，；………………………4分 ‎（II）由正弦定理，‎ ‎，，…………6分 ‎ ‎ 由得：，即，由余弦定理得，，‎ ‎，解得，……………8分 ‎ ‎ 由余弦定理得，即，‎ 得，当且仅当时，取等号，……………10分 ‎，面积的最大值为.………………12分 ‎20.【解析】（I）设 ………………1分 ‎ ………………3分 所以直线的斜率为 ； ………………4分 ‎（II）设圆心圆E的方程为 ，化解得 ‎， ………………6分 令得，即，所以或，‎ 不妨设 ………………8分 ‎，，‎ ‎ ………………10分 ‎，‎ 当且仅当，‎ 所以的最大值为. ………………12分 ‎21.【解析】（I）因为,,所以 ……………4分 ‎（II）,且当时，等价于 ‎ 当时， …………………………………………6分 令，则 ………8分 ‎ 再令，则，‎ ‎ 所以，在上单调递增，且,‎ ‎ 所以，在(1,2)上有唯一的零点，设该零点为，则，且，‎ 当时，，即；当时，，即，‎ 所以，在单调递减，在单调递增 ……………10分 所以，，‎ ‎ 而，故且，为整数 ‎ 所以，的最大值为2. …………………………………………12分 ‎22.【解析】（I）曲线的参数方程为，‎ 曲线的普通方程为………………………………………………………2分 曲线的极坐标方程为…………………………………………………………………………5分 ‎（II）设，则，故，…………………………………6分 点A，B在曲线上，，，………………………7分 ‎，……8分 当时，取到最大值……………………………………10分 ‎23.【解析】（I）…………………1分 由得；………2分， 由得；…………………3分，‎ 由得………4分， 综上所述，……………5分 ‎（II）为中的最大元素，……………………………………6分 ‎，…………8分 ‎（当且仅当时等号成立）‎ 即…………………………………………………10分 ‎ ‎ ‎ ‎ ‎ ‎