2017-2018学年吉林省实验中学高二下学期期末考试数学（理）试题 Word版 9页

吉林省实验中学 2017---2018 学年度下学期 高二年级数学学科（理）期末考试试题 一．选择题：本大题共 12 小题，每小题 5 分，在每小题给出的四个选项中，只有一项是符合 题目要求的。 1．设集合 M＝{－1,1}，N＝{x|x2－x＜6}，则下列结论正确的是( ) A．N⊆M B．M∩N＝ C．M⊆N D．M∩N＝R 2．函数 f(x)＝ x＋3＋log2(6－x)的定义域是( ) A．(6，＋∞) B．(－3,6) C．(－3，＋∞) D．[－3,6) 3．sin1，cos1，tan1 的大小关系是( ) A．sin1＜cos1＜tan1 B．tan1＜sin1＜cos1 C．cos1＜tan1＜sin1 D．cos1＜sin1＜tan1 4.下列函数中，定义域是 R 且为增函数的是( ) A．.y＝e－x B．y＝x3 C．y＝ln x D．y＝|x| 5．集合 A＝{x|x－2＜0}，B＝{x|x＜a}，若 A∩B＝A，则实数 a 的取值范围是( ) A．(－∞，－2] B．[－2，＋∞) C．(－∞，2] D．[2，＋∞) 6．设等比数列{an}中，前 n 项和为 Sn，已知 S3＝8，S6＝7，则 a7＋a8＋a9 等于( ) A.1 8 B．－1 8 C.57 8 D．55 8 7．执行如图所示的程序框图，输出的 s 值为( ) A．2 B．3 2 C．5 3 D．8 5 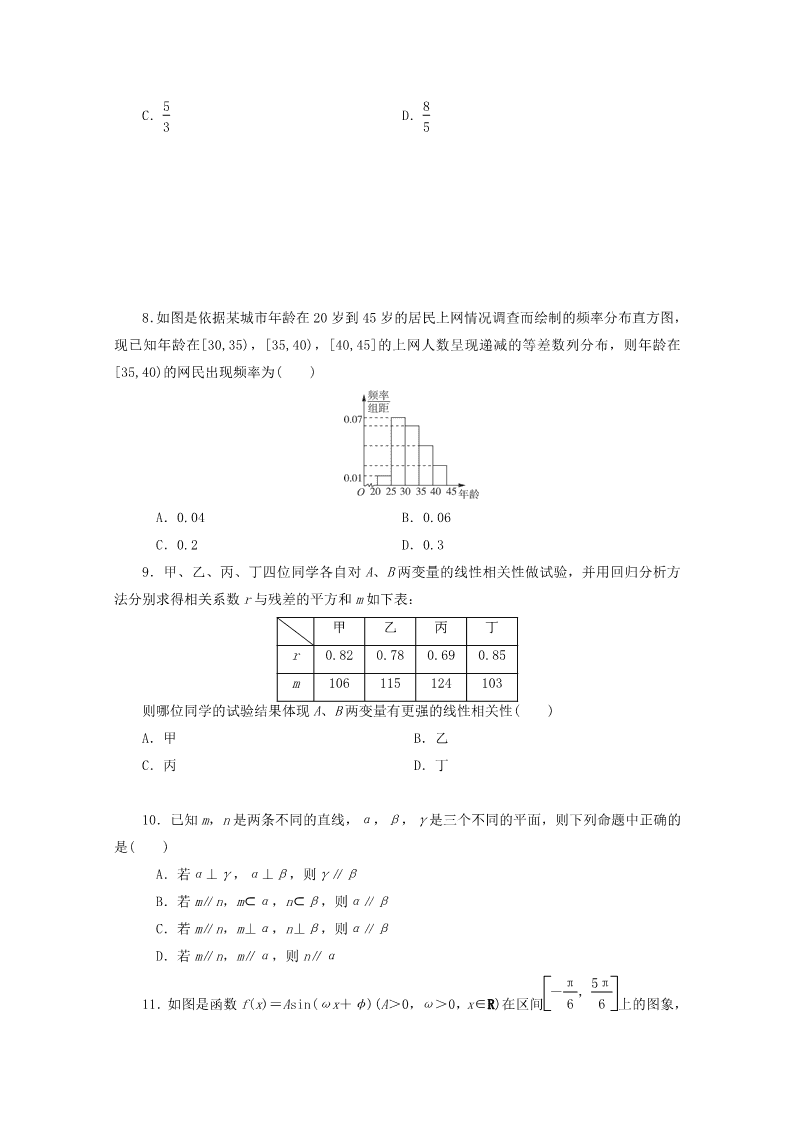8．如图是依据某城市年龄在 20 岁到 45 岁的居民上网情况调查而绘制的频率分布直方图， 现已知年龄在[30,35)，[35,40)，[40,45]的上网人数呈现递减的等差数列分布，则年龄在 [35,40)的网民出现频率为( ) A．0.04 B．0.06 C．0.2 D．0.3 9．甲、乙、丙、丁四位同学各自对 A、B 两变量的线性相关性做试验，并用回归分析方 法分别求得相关系数 r 与残差的平方和 m 如下表： 甲 乙 丙 丁 r 0.82 0.78 0.69 0.85 m 106 115 124 103 则哪位同学的试验结果体现 A、B 两变量有更强的线性相关性( ) A．甲 B．乙 C．丙 D．丁 10．已知 m，n 是两条不同的直线，α，β，γ是三个不同的平面，则下列命题中正确的 是( ) A．若α⊥γ，α⊥β，则γ∥β B．若 m∥n，m⊂α，n⊂β，则α∥β C．若 m∥n，m⊥α，n⊥β，则α∥β D．若 m∥n，m∥α，则 n∥α 11．如图是函数 f(x)＝Asin(ωx＋φ)(A＞0，ω＞0，x∈R)在区间 －π 6 ，5π 6 上的图象， 为了得到 y＝sinx(x∈R)的图象，只需将函数 f(x)的图象上所有的点( ) A．向左平移π 3 个单位长度，再把所得各点的横坐标缩短到原来的1 2 ，纵坐标不变 B．向右平移π 3 个单位长度，再把所得各点的横坐标伸长到原来的 2 倍，纵坐标不变 C．向左平移π 6 个单位长度，再把所得各点的横坐标缩短到原来的1 2 ，纵坐标不变 D．向右平移π 6 个单位长度，再把所得各点的横坐标伸长到原来的 2 倍，纵坐标不变 12．已知正棱锥 S－ABC 的底面边长为 4，高为 3，在正棱锥内任取一点 P，使得 VP－ABC<1 2 VS －ABC 的概率是( ) A.3 4 B．7 8 C．1 2 D．1 4 二．填空题：本大题共 4 小题，每小题 5 分。 13．已知向量 a＝(sinθ，－2)与 b＝(1，cosθ)互相垂直，其中θ∈ 0，π 2 ，则 cosθ＝________. 14.已知 f(x)是奇函数，g(x)＝ )( )(2 xf xf .若 g(2)＝3，则 g(－2)＝________. 15．如图，矩形 ABCD 中，AB＝2BC＝4，E 为边 AB 的中点，将△ADE 沿直线 DE 翻转成△A1DE. 若 M 为线段 A1C 的中点，则在△ADE 翻转过程中： ①|BM|是定值； ②点 M 在圆上运动； ③一定存在某个位置，使 DE⊥A1C； ④一定存在某个位置，使 MB∥平面 A1DE. 其中正确的命题是 16．若实数 x，y 满足 xy>0，则 x x＋y ＋ 2y x＋2y 的最大值为 三．解答题：解答应写出文字说明，证明过程或演算步骤。 17．（本小题满分 10 分） 已知函数 f(x)＝sin x＋π 12 ，x∈R. (1)求 f －π 4 的值； (2)若 cosθ＝4 5 ，θ∈ 0，π 2 ，求 f 2θ－π 3 的值． 18.（本小题满分 12 分） 数列{an}的前 n 项和 Sn＝2an－1，数列{bn}满足：b1＝3，bn＋1＝an＋bn(n∈N*)． (1)求证：数列{an}为等比数列； (2)求数列{bn}的前 n 项和 Tn. 19．（本小题满分 12 分） 已知|2x－3|≤1 的解集为[m，n]． (1)求 m＋n 的值； (2)若|x－a|＜m，求证：|x|＜|a|＋1. 20．（本小题满分 12 分） 海关对同时从 A，B，C 三个不同地区进口的某种商品进行抽样检测，从各地区进口 此种商品的数量(单位：件)如下表所示．工作人员用分层抽样的方法从这些商品中共抽 取 6 件样品进行检测. 地区 A B C 数量 50 150 100 (1)求这 6 件样品中来自 A，B，C 各地区商品的数量； (2)若在这 6 件样品中随机抽取 2 件送往甲机构进行进一步检测，求这 2 件商品来自相同 地区的概率． 21．（本小题满分 12 分） 在△ABC 中，角 A，B，C 的对边分别为 a，b，c，已知(a－3b)cosC＝c(3cosB－cosA)． (1)求sinB sinA 的值； (2)若 c＝ 7a，求角 C 的大小． 22．(本小题满分 12 分) 设函数 f(x)＝kax－a－x(a>0 且 a≠1)是定义域为 R 的奇函数． (1)若 f(1)>0，试求不等式 f(x2＋2x)＋f(x－4)>0 的解集； (2)若 f(1)＝3 2 ，且 g(x)＝a2x＋a－2x－4f(x)，求 g(x)在[1，＋∞)上的最小值． 吉林省实验中学 2017---2018 学年度下学期 高二年级数学学科（理）期末考试试题答案 1-6 CDDBDA 7-12 CCDCDB 13. 5 5 14.-1 15.①②④ 16.4－2. 17．已知函数 f(x)＝sin π 12，x∈R. (1)求 f π 4 的值；(2)若 cosθ＝ 4 5，θ∈ π 2 ，求 f π 3 的值． 解：(1)f π 4 ＝sin π 12＝sin π 6 ＝－ 1 2. (2)f π 3 ＝sin π 12＝sin π 4 ＝ 2 2(sin2θ－cos2θ)． 因为 cosθ＝ 4 5，θ∈ π 2 ，所以 sinθ＝ 3 5， 所以 sin2θ＝2sinθcosθ＝ 24 25，cos2θ＝cos2θ－sin2θ＝ 7 25， 所以 f π 3 ＝ 2 2(sin2θ－cos2θ)＝ 2 2× 7 25＝ 2 50. 18.数列{an}的前 n 项和 Sn＝2an－1，数列{bn}满足：b1＝3，bn＋1＝an＋bn (n∈N*)． (1)求证：数列{an}为等比数列；(2)求数列{bn}的前 n 项和 Tn. 解析 (1)证明：∵Sn＝2an－1，n∈N*，∴Sn＋1＝2an＋1－1.两式相减得 an＋1＝2an＋1－2an. ∴an＋1＝2an，n∈N*.由 a1＝1，知 an≠0， ∴ an＋1 an ＝2.由定义知{an}是首项为 1，公比为 2 的等比数列． (2)由(1)知，an＝2n－1，bn＋1＝2n－1＋bn， ∴bn＋1－bn＝2n－1. ∴b2－b1＝20，b3－b2＝21，b4－b3＝22，… bn－bn－1＝2n－2，等式左右两边相加得 bn＝b1＋20＋21＋…＋2n－2＝3＋ 1－2n－1 1－2 ＝2n－1＋2. ∴Tn＝(20＋2)＋(21＋2)＋…＋(2n－1＋2)＝(20＋21＋…＋2n－1)＋2n＝2n＋2n－1. 19．已知|2x－3|≤1 的解集为[m，n]． (1)求 m＋n 的值； (2)若|x－a|＜m，求证：|x|＜|a|＋1. 解：(1)不等式|2x－3|≤1 可化为－1≤2x－3≤1， 解得 1≤x≤2，所以 m＝1，n＝2，m＋n＝3. (2)证明：若|x－a|＜1，则|x|＝|x－a＋a|≤|x－a|＋|a|＜|a|＋1.即|x|＜|a|＋1. 20．海关对同时从 A，B，C 三个不同地区进口的某种商品进行抽样检测，从各地区进口 此种商品的数量(单位：件)如下表所示．工作人员用分层抽样的方法从这些商品中共抽取 6 件样品进行检测. 地区 A B C 数量 50 150 100 (1)求这 6 件样品中来自 A，B，C 各地区商品的数量； (2)若在这 6 件样品中随机抽取 2 件送往甲机构进行进一步检测，求这 2 件商品来自相同 地区的概率． 解析 (1)因为样本容量与总体中的个体数的比是 6 50＋150＋100＝ 1 50，所以样本中包含三 个地区的个体数量分别是 50× 1 50＝1,150× 1 5＝3,100× 1 50＝2. 所以 A，B，C 三个地区的商品被选取的件数分别为 1,3,2. (2)设 6 件来自 A，B，C 三个地区的样品分别为：A；B1，B2，B3；C1，C2. 则抽取的这 2 件商品构成的所有基本事件为： {A，B1}，{A，B2}，{A，B3}，{A，C1}，{A，C2}，{B1，B2}，{B1，B3}，{B1，C1}，{B1，C2}， {B2，B3}，{B2，C1}，{B2，C2}，{B3，C1}，{B3，C2}，{C1，C2}，共 15 个． 每个样品被抽到的机会均等，因此这些基本事件的出现是等可能的． 记事件 D：“抽取的这 2 件商品来自相同地区”， 则事件 D 包含的基本事件有 {B1，B2}，{B1，B3}，{B2，B3}，{C1，C2}，共 4 个． 所以 P(D)＝ 4 15，即这 2 件商品来自相同地区的概率为 4 15. 21．在△ABC 中，角 A，B，C 的对边分别为 a，b，c，已知(a－3b)cosC＝c(3cosB－cosA)． (1)求 sinB sinA的值； (2)若 c＝a，求角 C 的大小． 解：(1)由正弦定理得，(sinA－3sinB)cosC＝sinC(3cosB－cosA)， ∴sinAcosC＋cosAsinC＝3sinCcosB＋3cosCsinB， 即 sin(A＋C)＝3sin(C＋B)，即 sinB＝3sinA，∴ sinB sinA＝3. (2)由(1)知 b＝3a，∵c＝a， ∴cosC＝ a2＋b2－c2 2ab ＝ a2＋9a2－7a2 2×a×3a ＝ 3a2 6a2＝ 1 2，∵C∈(0，π)，∴C＝ π 3 . 22．(本小题满分 12 分) 设函数 f(x)＝kax－a－x(a>0 且 a≠1)是定义域为 R 的奇函数． (1)若 f(1)>0，试求不等式 f(x2＋2x)＋f(x－4)>0 的解集； (2)若 f(1)＝ 3 2，且 g(x)＝a2x＋a－2x－4f(x)，求 g(x)在[1，＋∞)上的最小值． 解析 ∵f(x)是定义域为 R 的奇函数，∴f(0)＝0，∴k－1＝0，∴k＝1. (1)∵f(1)>0，∴a－ 1 a>0. 又 a>0 且 a≠1，∴a>1. ∵k＝1，∴f(x)＝ax－a－x. 当 a>1 时，y＝ax 和 y＝－a－x 在 R 上均为增函数， ∴f(x)在 R 上为增函数． 原不等式可化为 f(x2＋2x)>f(4－x)，∴x2＋2x>4－x，即 x2＋3x－4>0. ∴x>1 或 x<－4. ∴不等式的解集为{x|x>1 或 x<－4}． (2)∵f(1)＝ 3 2，∴a－ 1 a＝ 3 2，即 2a2－3a－2＝0. ∴a＝2 或 a＝－ 1 2(舍去)． ∴g(x)＝22x＋2－2x－4(2x－2－x)＝(2x－2－x)2－4(2x－2－x)＋2. 令 t＝h(x)＝2x－2－x(x≥1)， 则 g(t)＝t2－4t＋2. ∵t＝h(x)在[1，＋∞)上为增函数(由(1)可知)， ∴h(x)≥h(1)＝ 3 2，即 t≥ 3 2. ∵g(t)＝t2－4t＋2＝(t－2)2－2，t∈[ 3 2，＋∞)， ∴当 t＝2 时，g(t)取得最小值－2，即 g(x)取得最小值－2，此时 x＝log2(1＋)． 故当 x＝log2(1＋)时，g(x)有最小值－2.