高一数学（人教A版）必修4能力提升：2-3-1 平面向量基本定理 8页

能 力 提 升 一、选择题 ‎1．在四边形ABCD中，＝a＋2b，＝－‎4a－b，＝－‎5a－3b，其中a、b不共线，则四边形ABCD为(　　)‎ A．平行四边形 B．矩形 C．梯形 D．菱形 ‎[答案]　C ‎[解析]　∵＝＋＋＝a＋2b－‎4a－b－‎5a－3b＝－‎8a－2b＝2(－‎4a－b)＝2，即＝2，‎ ‎∴AD∥BC且AD≠BC，故选C.‎ ‎2．已知＝a，＝b，C为线段AB上距A较近的一个三等分点，D为线段CB上距C较近的一个三等分点，则用a、b表示为(　　)‎ A.(‎4a＋5b)‎ B.(‎9a＋7b)‎ C.(‎2a＋b)‎ D.(‎3a＋b)‎ ‎[答案]　A ‎[解析]　利用向量加法和减法的几何意义和平面向量基本定理求解．‎ ‎∵＝＋，＝＋ ‎＝＋＝＋＝.‎ 而＝b－a，∴＝b－a，‎ ‎∴＝＋＝a＋(b－a)＝a＋b.‎ ‎3．如图所示，在平行四边形ABCD中，AC与BD交于点O，E是线段OD的中点，AE的延长线与CD交于点F.若＝a，＝b，则＝(　　)‎ A.a＋b B.a＋b C.a＋b D.a＋b ‎[答案]　D ‎[解析]　∵＝＋＝a＋＝a＋(b－a)＝a＋b.‎ ‎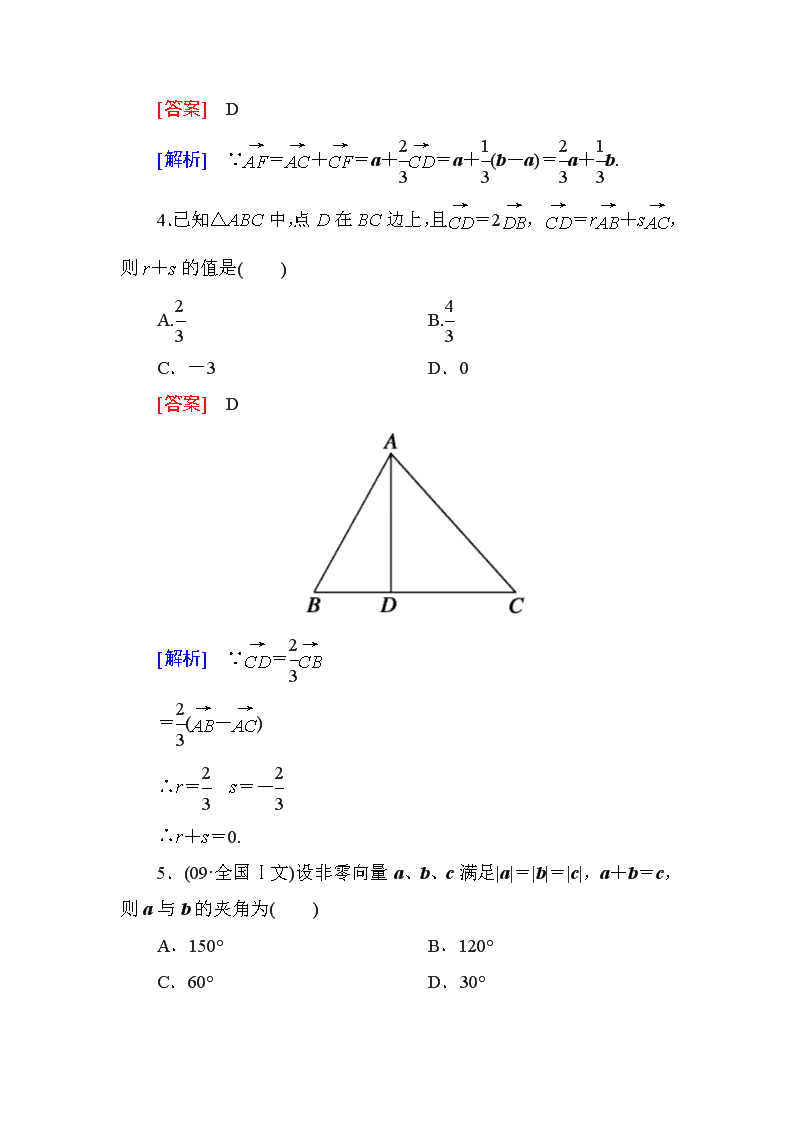4．已知△ABC中，点D在BC边上，且＝2，＝r＋s，则r＋s的值是(　　)‎ A. B. ‎ C．－3 D．0‎ ‎[答案]　D ‎[解析]　∵＝ ‎＝(－)‎ ‎∴r＝　s＝－ ‎∴r＋s＝0.‎ ‎5．(09·全国Ⅰ文)设非零向量a、b、c满足|a|＝|b|＝|c|，a＋b＝c，则a与b的夹角为(　　)‎ A．150° B．120° ‎ C．60° D．30°‎ ‎[答案]　B ‎[解析]　∵|a|＝|b|＝|c|≠0，且a＋b＝c ‎∴如图所示就是符合题设条件的向量，易知OACB是菱形，△‎ OBC和△OAC都是等边三角形．‎ ‎∴a与b的夹角为120°.‎ ‎6．(2011～2012·合肥市)如图，△ABC中，AD＝DB，AE＝EC，CD与BE交于F，设＝a，＝b，＝xa＋yb，则(x，y)为(　　)‎ A. B. C. D. ‎[答案]　C ‎[解析]　设＝λ，∵E、D分别为AC、AB的中点，∴＝＋＝－a＋b，‎ ＝＋＝(b－a)＋λ(a－b)‎ ‎＝a＋(1－λ)b，‎ ‎∵与共线，∴＝，∴λ＝，‎ ‎∴＝＋＝b＋＝b＋ ‎＝a＋b，故x＝，y＝.‎ 二、填空题 ‎7．向量a与b的夹角为25°，则‎2a与－b的夹角θ＝________.‎ ‎[答案]　155°‎ ‎[解析]　作＝a，＝b，则∠AOB＝25°，如图所示．‎ 延长OA到C，使OA＝AC，则＝‎2a.‎ 延长BO到D，使OD＝BO，则＝－b.‎ 则θ＝∠DOA，又∠DOA＋∠AOB＝180°，则∠DOA＝180°－25°＝155°，则θ＝155°.‎ ‎8．已知e1、e2是两个不共线的向量，而a＝k2e1＋(1－k)e2与b＝2e1＋3e2是两个共线向量，则实数k＝________.‎ ‎[答案]　－2或 ‎[解析]　由题设知＝，∴3k2＋5k－2＝0.‎ 解得k＝－2或.‎ ‎9．已知向量a和向量b不共线，且m＋n＝a，m－n＝b，则m＝________，n＝________.(用a、b表示)‎ ‎[答案]　　 ‎[解析]　解方程组 得m＝，n＝ 三、解答题 ‎10．如图，梯形ABCD中，AB∥CD，且AB＝2CD，M、N分别是DC和AB的中点，若＝a，＝b，试用a、b表示、，.‎ ‎[解析]　如图所示，连接CN，则四边形ANCD是平行四边形．‎ 则＝＝＝a，‎ ＝－＝－＝b－a，‎ ＝－＝－－ ‎＝－－ ‎＝a－b.‎ ‎11．已知|a|＝|b|＝2，且a与b的夹角为120°，求a＋b与a的夹角，a－b与a的夹角．‎ ‎[解析]　如图，作＝a，＝b，且∠AOB＝120°，‎ 以OA，OB为邻边作▱OACB，‎ 则＝＋＝a＋b，＝－＝a－b，‎ ＝＝a.‎ 因为|a|＝|b|＝2，所以△OAB为等腰三角形，‎ 所以∠OAB＝30°‎ 即a－b与a的夹角为30°.‎ 因为|a|＝|b|，所以平行四边形OACB为菱形，‎ 所以OC⊥AB，所以∠COA＝60°，‎ 即a＋b与a的夹角为60°.‎ ‎12．设M、N、P是△ABC三边上的点，它们使＝，＝，＝，若＝a，＝b，试用a、b将、、表示出来．‎ ‎[解析]　如图，＝－＝－－＝－－(－)＝－＝b－a.‎ 同理可得＝a－b，‎ ＝－＝－(＋)＝a＋b.‎