【数学】2019届文科一轮复习人教A版6-重点强化课3不等式及其应用教案 5页

重点强化课(三)　不等式及其应用 ‎ (对应学生用书第85页)‎ ‎ [复习导读]　本章的主要内容是不等式的性质，一元二次不等式及其解法，简单的线性规划问题，基本不等式及其应用，针对不等式具有很强的工具性，应用广泛，解法灵活的特点，应加强不等式基础知识的复习，要弄清不等式性质的条件与结论；一元二次不等式是解决问题的重要工具，如利用导数研究函数的单调性，往往归结为解一元二次不等式问题；函数、方程、不等式三者密不可分，相互转化，因此应加强函数与方程思想在不等式中应用的训练．‎ 重点1　一元二次不等式的综合应用 ‎　(1)(2018·烟台模拟)函数y＝的定义域为(　　)‎ A．(－∞，1]　　　　　　 B．[－1,1]‎ C．[1,2)∪(2，＋∞) D．∪ ‎(2)已知函数f(x)＝则满足不等式f(1－x2)>f(2x)的x的取值范围是__________．‎ ‎(1)D　(2)(－1，－1)　[(1)由题意得解得即－1≤x≤1且x≠－，所以函数的定义域为，故选D.‎ ‎(2)由题意得或 解得－10时，f(x)＝x2－4x，则不等式f(x)>x的解集用区间表示为__________. 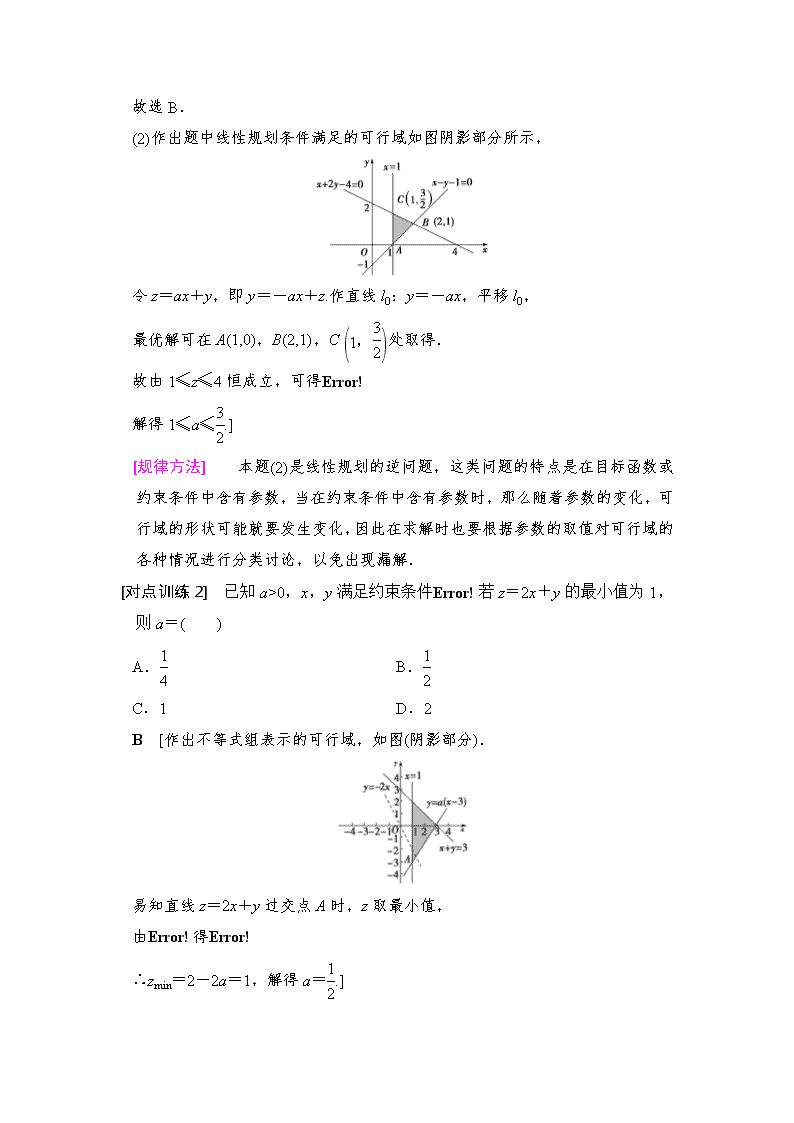【导学号：79170202】‎ ‎(－5,0)∪(5，＋∞)　[由于f(x)为R上的奇函数，‎ 所以当x＝0时，f(0)＝0；当x<0时，－x>0，‎ 所以f(－x)＝x2＋4x＝－f(x)，即f(x)＝－x2－4x，‎ 所以f(x)＝ 由f(x)>x，可得 或 解得x>5或－50，x，y满足约束条件若z＝2x＋y的最小值为1，则a＝(　　)‎ A． B． C．1 D．2‎ B　[作出不等式组表示的可行域，如图(阴影部分)．‎ 易知直线z＝2x＋y过交点A时，z取最小值，‎ 由得 ‎∴zmin＝2－2a＝1，解得a＝.]‎ 重点3　基本不等式的综合应用 ‎　(2016·江苏高考节选)已知函数f(x)＝ax＋bx(a>0，b>0，a≠1，b≠1)．设a＝2，b＝.‎ ‎(1)求方程f(x)＝2的根；‎ ‎(2)若对于任意x∈R，不等式f(2x)≥mf(x)－6恒成立，求实数m的最大值. ‎ ‎【导学号：79170203】‎ ‎[解]　因为a＝2，b＝，所以f(x)＝2x＋2－x. 2分 ‎(1)方程f(x)＝2，即2x＋2－x＝2，亦即(2x)2－2×2x＋1＝0，所以(2x－1)2＝0，即2x＝1，解得x＝0. 5分 ‎(2)由条件知f(2x)＝22x＋2－2x＝(2x＋2－x)2－2＝(f(x))2－2.‎ 因为f(2x)≥mf(x)－6对于x∈R恒成立，且f(x)>0，‎ 所以m≤对于x∈R恒成立. 8分 而＝f(x)＋≥2＝4，且＝4，所以m≤4，故实数m的最大值为4. 12分 ‎[规律方法]　　基本不等式综合应用中的常见类型及求解方法：‎ ‎(1)应用基本不等式判断不等式是否成立或比较大小．解决此类问题通常将所给不等式(或式子)变形，然后利用基本不等式求解．‎ ‎(2)条件不等式问题．通过条件转化成能利用基本不等式的形式求解．‎ ‎(3)求参数的值或范围．观察题目特点，利用基本不等式确定相关成立条件，从而得到参数的值或范围．‎ ‎[对点训练3]　(1)(2018·南昌模拟)已知x＞0，y＞0，x＋3y＋xy＝9，则x＋3y的最小值为________．‎ ‎(2)已知正数x，y满足x＋2y＝2，则的最小值为__________．‎ ‎(1)6　(2)9　[(1)法一：(消元法)‎ 因为x＞0，y＞0，所以0＜y＜3，‎ 所以x＋3y＝＋3y ‎＝＋3(y＋1)－6≥2－6＝6，‎ 当且仅当＝3(y＋1)，‎ 即y＝1，x＝3时，(x＋3y)min＝6.‎ 法二：(不等式法)‎ ‎∵x＞0，y＞0，‎ ‎9－(x＋3y)＝xy＝x·(3y)≤·2，‎ 当且仅当x＝3y时等号成立．‎ 设x＋3y＝t＞0，则t2＋12t－108≥0，‎ 解得t≥6或t≤－18(舍去)‎ 故当x＝3，y＝1时，x＋3y的最小值为6.‎ ‎(2)由已知得＝1.‎ 则＝＋＝ ‎＝≥(10＋2 )＝9，‎ 当且仅当x＝，y＝时取等号．]‎