【数学】2018届一轮复习人教A版实际问题的函数建模问题学案 8页

‎4.2　实际问题的函数建模 问题导学 一、二次函数模型的应用 活动与探究1‎ 某租赁公司出租同一型号的设备40套，当每套月租金为270元时，恰好全部租出．在此基础上，每套月租金每增加10元，就少租出1套设备，而未租出的设备每月需支付各种费用每套20元．设每套设备实际月租金为x元(x≥270元)，月收益为y元(总收益＝设备租金收入－未租出设备费用)．‎ ‎(1)求y与x之间的函数关系式；‎ ‎(2)当x为何值时，月收益最大？最大值是多少？‎ 迁移与应用 某旅游公司的最大接待量为1 000人，为保证公司正常运作，实际的接待量x要小于1 000，留出适当的空闲量(如：当接待量为800人时，则空闲量为200人)，空闲量与最大接待量的比值叫作空闲率．已知该公司4月份接待游客的月增加量y(人)和实际接待量x(人)与空闲率的乘积成正比．(设比例系数k＞0)‎ ‎(1)写出y关于x的函数关系式，并指出定义域；‎ ‎(2)当k＝时，求4月份游客日增加量的最大值．‎ 在函数模型中，二次函数模型占有重要的地位，根据实际问题列出二次函数解析式后，通常可利用配方法求出其最值，但应注意函数自变量的取值范围，即应在函数定义域的前提下求最值．‎ 二、分段函数模型 活动与探究2‎ 某医药研究所开发一种新药，如果成年人按规定的剂量服用，据监测，服药后每毫升血液中的含药量y(毫克)与时间t(小时)之间近似满足如图所示的曲线．‎ ‎(1)写出服药后y与t之间的函数关系式y＝f(t)；‎ ‎(2)进一步测定：每毫升血液中含药量不少于0.25毫克时，药物对治疗疾病有效．求服药一次治疗疾病的有效时间．‎ 迁移与应用 某公司生产一种电子仪器的固定成本为20 000元，每生产一台仪器需要增加投入100元，已知总收益满足函数：‎ R(x)＝其中x是仪器的月产量．‎ ‎(1)将利润表示为月产量的函数f(x)．‎ ‎(2)当月产量为何值时，公司所获利润最大？最大利润为多少元？(总收益＝总成本＋利润)‎ 分段函数模型应用的关键是确定分段的各边界点，即明确自变量的取值区间，对每一区间进行分类讨论，从而写出函数的解析式．需注意分段函数的最值，是各区间上解析式所得最值的最大者或最小者．‎ 三、指数函数模型的应用 活动与探究3[ ]‎ 有一种放射性元素，因放出射线，其质量在不断减少，经测算，每年衰减的百分率相同．若该元素最初的质量为‎50 g，经过一年后质量变为‎40 g.‎ ‎(1)设x(x≥0)年后，这种放射性元素的质量为y g，写出y关于x的表达式．‎ ‎(2)求经过多长时间，这种放射性元素的质量变为原来的一半？(精确到0.1年，参考数据：lg 2≈0.301 0，lg 3≈0.477 1)‎ 迁移与应用 某纯净水制造厂在净化水的过程中，每增加一次过滤可减少水中杂质20%.‎ ‎(1)写出水中杂质含量y与过滤的次数x之间的函数关系式；‎ ‎(2)要使水中杂质减少到原来的5%以下，则至少需要过滤几次？(参考数据：lg 2＝0.301 0)‎ 实际问题中，有关人口增长、银行利率、细胞分裂等增长率问题常可以用指数函数模型来表示，在建立函数模型时，注意用列举、归纳等方法来探求内在的规律．‎ 四、对数函数模型的应用 活动与探究4‎ 大西洋鲑鱼每年都要逆流而上2 ‎000 m，游回产地产卵．研究鲑鱼的科学家发现鲑鱼的游速可以表示为函数y＝log3，单位是m/s，其中x表示鲑鱼的耗氧量的单位数． ‎ ‎(1)当一条鲑鱼的耗氧量是8 100个单位时，它的游速是多少？‎ ‎(2)计算一条鲑鱼静止时耗氧量的单位数；[ ]‎ ‎(3)若鲑鱼A的游速大于鲑鱼B的游速，问这两条鲑鱼谁的耗氧量较大？并说明理由．‎ 迁移与应用 燕子每年秋天都要从北方飞向南方过冬，研究燕子的科学家发现，两岁燕子的飞行速度可以表示为函数v＝5log2，单位是m/s，其中Q表示燕子的耗氧量．‎ ‎(1)燕子静止时的耗氧量是多少个单位？‎ ‎(2)当一只燕子的耗氧量是80个单位时，它的飞行速度是多少？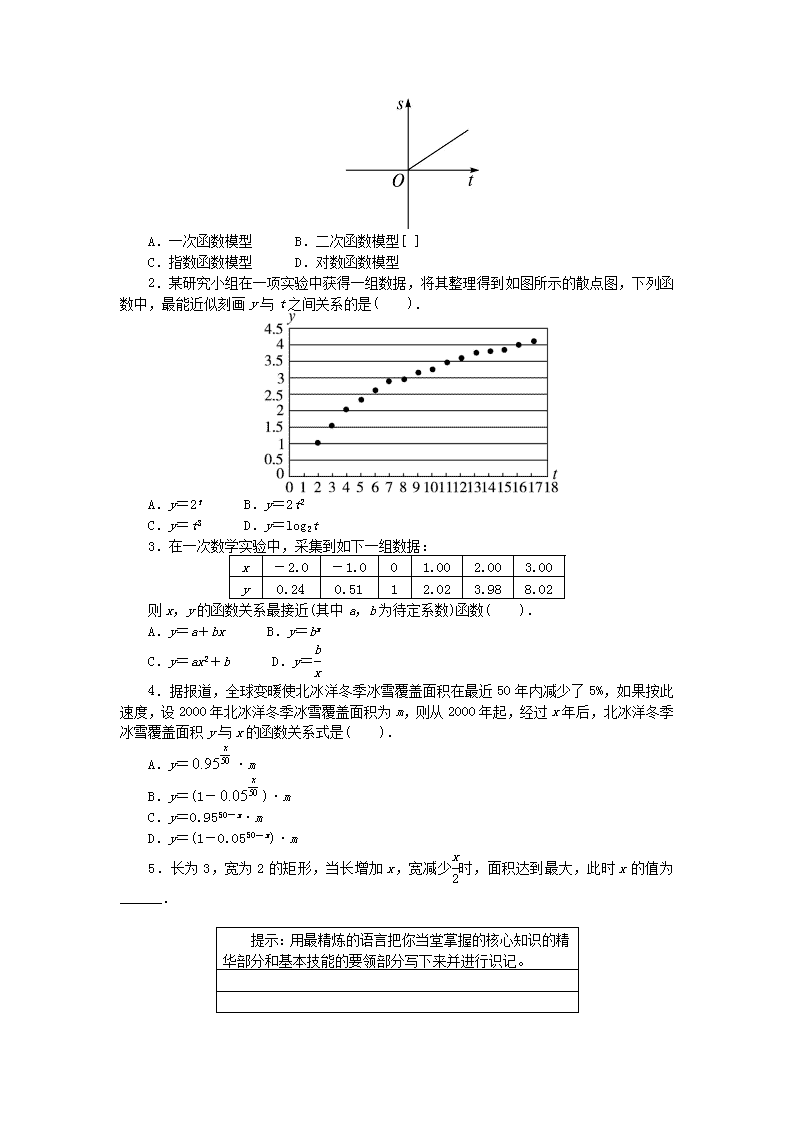‎ 有关对数函数的应用题一般都会给出函数关系式，要求根据实际情况求出函数关系式中的参数，或给出具体情境，从中提炼出数据，代入关系式求值，然后根据所求值回答其实际意义．‎ 当堂检测 ‎1．一辆汽车的行驶路程s关于时间t变化的图像如图所示，那么图像所对应的函数模型是(　　)．‎ A．一次函数模型 B．二次函数模型[ ]‎ C．指数函数模型 D．对数函数模型 ‎2．某研究小组在一项实验中获得一组数据，将其整理得到如图所示的散点图，下列函数中，最能近似刻画y与t之间关系的是(　　)．‎ A．y＝2t B．y＝2t2‎ C．y＝t3 D．y＝log2t ‎3．在一次数学实验中，采集到如下一组数据：‎ x ‎－2.0‎ ‎－1.0‎ ‎0‎ ‎1.00‎ ‎2.00‎ ‎3.00‎ y ‎0.24‎ ‎0.51‎ ‎1‎ ‎2.02‎ ‎3.98‎ ‎8.02‎ 则x，y的函数关系最接近(其中a，b为待定系数)函数(　　)．‎ A．y＝a＋bx B．y＝bx C．y＝ax2＋b D．y＝ ‎4．据报道，全球变暖使北冰洋冬季冰雪覆盖面积在最近50年内减少了5%，如果按此速度，设2000年北冰洋冬季冰雪覆盖面积为m，则从2000年起，经过x年后，北冰洋冬季冰雪覆盖面积y与x的函数关系式是(　　)．‎ A．y＝·m B．y＝(1－)·m C．y＝0.9550－x·m D．y＝(1－0.0550－x)·m ‎5．长为3，宽为2的矩形，当长增加x，宽减少时，面积达到最大，此时x的值为______．‎ 提示：用最精炼的语言把你当堂掌握的核心知识的精华部分和基本技能的要领部分写下来并进行识记。‎ 答案：‎ 课前预习导学 ‎【预习导引】‎ ‎1．f(a)·f(b)＜0　中点　小区间 ‎2．反号　中点　精度　任意一个数 ‎ 预习交流1　提示：利用二分法求得的零点也可能是准确值，例如f(x)＝x2－1在[0,2]上的零点；利用二分法求方程在[a，b]内的近似解时，如果方程的根有多个，那么一次只能求得其中的一个．‎ 预习交流2　提示：(1)要看清题目要求的精度，它决定着二分法步骤的结束．‎ ‎(2)初始区间的选定一般在两个整数间，不同的初始区间结果是相同的，但二分的次数却相差较大．‎ ‎(3)用二分法求出的零点一般是零点的近似值，但并不是所有函数都可以用二分法求零点，必须满足在区间[a，b]上连续不断，且f(a)·f(b)＜0这样条件的函数才能用二分法求得零点的近似值．‎ 课堂合作探究 ‎【问题导学】‎ 活动与探究1　(1)B　(2)1.437 5　解析：(1)从图像上可以看出B中的函数值在零点两侧都小于0，所以不能用二分法求函数的零点．‎ ‎(2)由于f(1.25)·f(1.5)＜0，所以近似解位于区间[1.25,1.5]，又f(1.375)·f(1.5)＜0，所以近似解位于区间[1.375,1.5]，因此下一次计算应取m＝＝1.437 5.‎ 迁移与应用　(1)B　(2)A　解析：(2)由于f(－2)＝(－2)3＋5＝－3＜0，f(1)＝13＋5＝6＞0，f(－2)·f(1)＜0，所以初始区间可取[－2,1]．‎ 活动与探究2　思路分析：先确定f(x)＝lg x－2－x＋1的零点所在的大致区间，再用二分法求解．‎ 解：令f(x)＝lg x－2－x＋1，函数f(x)的定义域为(0，＋∞)．‎ 因为函数f(x)在(0，＋∞)上是增函数(证明略)，所以f(x)至多有一个零点．‎ 又因为f(1)＝0.5＞0，f(0.1)≈－0.933＜0，所以方程在[0.1,1]内有唯一实数解．‎ 使用二分法求解，如下表：‎ 次数 左端点 左端点函数值 右端点 右端点函数值 第1次 ‎0.1‎ ‎－0.933 033‎ ‎1‎ ‎0.5‎ 第2次 ‎0.1‎ ‎－0.933 033‎ ‎0.55‎ ‎0.057 343‎ 第3次 ‎0.325‎ ‎－0.286 415‎ ‎0.55‎ ‎0.057 343‎ 第4次 ‎0.437 5‎ ‎－0.097 435‎ ‎0.55‎ ‎0.057 343‎ 第5次 ‎0.493 75‎ ‎－0.016 670‎ ‎0.55‎ ‎0.057 343‎ 至此，得到区间[0.493 75,0.55]，其长度0.55－0.493 75＝0.056 25＜0.1，由于要求的精度为0.1，则这一区间内的任一数都可作为方程的近似解，不妨取0.5作为方程的近似解．‎ 迁移与应用　解：用二分法逐次计算，列表如下：[ ‎ 次数 左端点 左端点函数值 右端点[ ]‎ 右端点函数值 第1次 ‎1‎ ‎－1‎ ‎1.5‎ ‎0.875‎ 第2次 ‎1.25‎ ‎－0.296 875‎ ‎1.5‎ ‎0.875‎ 第3次 ‎1.25‎ ‎－0.296 875‎ ‎1.375‎ ‎0.224 609‎ 第4次[ ]‎ ‎1.312 5‎ ‎－0.051 514‎ ‎1.375‎ ‎0.224 609‎ 由于区间[1.312 5,1.375]的长度1.375－1.312 5＝0.062 5＜0.1，所以当精度为0.1时，该区间内的每一个数都是函数的近似零点，不妨取1.3作为函数f(x)在[1,1.5]内的近似零点．‎ ‎【当堂检测】‎ ‎1．C　2．B ‎3．取区间[1,2]的中点c＝＝.‎ ‎4．[2,2.5]　解析：令f(x)＝x3－2x－5，f(2)＝－1＜0，f(2.5)＝2.53－10＞0，所以有根区间是[2,2.5]．‎ ‎5．2.53　解析：由于区间[2.531 25,2.539 062 5]的长度为2.539 062 5－2.531 25＝0.007 812 5＜0.01，所以精度为0.01时，方程的一个正的近似解是2.53.‎ ‎§2　实际问题的函数建模 课前预习导学 ‎【预习导引】‎ ‎1．函数 ‎2．性质　整体特征　函数表达式　实验　数据　拟合 ‎3．(1)方法　知识 预习交流　提示：(1)直线模型：一次函数模型y＝kx＋b(k≠0)，其图像增长特点是直线式上升(x的系数k＞0)，通过图像可以直观地认识它，特例是正比例函数模型y＝kx(k＞0)．‎ ‎(2)反比例函数模型：y＝(k＞0)型，其增长特点是y随x的增大而减小．‎ ‎(3)指数函数模型：y＝a·bx＋c(b＞0，且b≠1，a≠0)，其增长特点是随着自变量的增大，函数值增大的速度越来越快(底数b＞1，a＞0)，常形象地称为指数爆炸．‎ ‎(4)对数函数模型：y＝mlogax＋n(a＞0，a≠1，m≠0)，其增长特点是随着自变量的增大，函数值增大越来越慢(底数a＞1，m＞0)．‎ ‎(5)幂函数模型：y＝a·xn＋b(a≠0)，其中最常见的是二次函数模型：y＝ax2＋bx＋c(a≠0)，其特点是随着自变量的增大，函数值先减小后增大(a＞0)．‎ 在以上几种函数模型的选择与建立时，要注意函数图像的直观运用，分析图像特点，分析变量x的范围，同时还要与实际问题结合，如取整等．‎ 课堂合作探究 ‎【问题导学】‎ 活动与探究1　思路分析：(1)利用总收益＝设备租金收入－未租出设备费用列出函数关系式；‎ ‎(2)转化为求相应二次函数的最大值．‎ 解：(1)设每套设备实际月租金为x元(x≥270元)，则未租出的设备为套，未租出的设备费用为元；租出的设备为套，月租金总额为元．‎ 所以y＝x－×20‎ ‎＝－0.1x2＋65x＋540.‎ ‎(2)由(1)得y＝－0.1x2＋65x＋540＝－0.1(x－325)2＋11 102.5.所以当x＝325时，y取最大值为11 102.5，‎ 即当每套设备实际月租金为325元时，月收益达到最大值11 102.5元．‎ 迁移与应用　解：(1)由题意知，当实际接待量为x人时，空闲率为.故y关于x的函数关系式为y＝kx·(k＞0)，函数的定义域为0＜x＜1 000.‎ ‎(2)∵当k＝时，y＝x· ‎＝(－x2＋1 000x)‎ ‎＝[－(x－500)2＋250 000]‎ ‎＝－(x－500)2＋25，‎ ‎∴当x＝500时，ymax＝25.‎ ‎∴4月份游客日增加量的最大值为25人．‎ 活动与探究2　思路分析：(1)由于在t∈[0,1]，t∈(1，＋∞)上的函数模型已知，只须用待定系数法求出相应的k和a的值，即可用分段函数写出y＝f(t)．‎ ‎(2)令f(t)≥0.25，解出t的范围，进而确定治疗疾病的有效时间．‎ 解：(1)由函数图像可知，当t∈[0,1]时，函数的解析式为y＝kt(k≠0)，‎ 将M(1,4)代入得k＝4，所以y＝4t.‎ 又当t∈(1，＋∞)时，函数的解析式为y＝t－a，‎ 将点(3,1)代入得a＝3.所以y＝t－3.‎ 综上，y＝f(t)＝ ‎(2)当0≤t≤1时，由f(t)＝4t≥0.25，得≤t≤1；‎ 当t＞1时，由f(t)＝t－3≥0.25，得1＜t≤5，‎ 因此≤t≤5.‎ 所以服药一次治疗疾病的有效时间为5－＝(个)小时．‎ 迁移与应用　解：(1)每月产量为x台，‎ 则总成本为20 000＋100x，从而 f(x)＝ ‎(2)当0≤x≤400时，f(x)＝－(x－300)2＋25 000，‎ 所以当x＝300时，有最大值25 000；‎ 当x＞400时，f(x)＝60 000－100x是减少的，‎ f(x)＜60 000－100×400＝20 000＜25 000，‎ 所以当月产量为300台时，公司所获利润最大，最大利润为25 000元．‎ 活动与探究3　思路分析：本题属于降低率问题，可建立指数函数模型解决．‎ 解：(1)由题意知，每经过一年该放射性元素衰减的百分率为＝20%，‎ 所以y＝50(1－20%)x，即y＝50×0.8x(x≥0)．‎ ‎(2)由题意知50×0.8x＝25，‎ 即0.8x＝0.5.‎ 则lg 0.8x＝lg 0.5，‎ 所以xlg 0.8＝lg 0.5，‎ 即x＝＝≈≈3.1.‎ 故约经过3.1年，这种放射性元素的质量变为原来的一半．‎ 迁移与应用　解：(1)设刚开始水中杂质含量为1，‎ 第1次过滤后，y＝1－20%；‎ 第2次过滤后，y＝(1－20%)(1－20%)＝(1－20%)2；‎ 第3次过滤后，y＝(1－20%)2(1－20%)＝(1－20%)3；‎ ‎……‎ 第x次过滤后，y＝(1－20%)x.‎ 所以y＝(1－20%)x＝0.8x(x≥1，x∈N)．‎ ‎(2)由(1)得0.8x＜5%，‎ 所以x＞log0.80.05＝＝＝≈13.4.‎ 故至少需要过滤14次．‎ 活动与探究4　思路分析：(1)将x＝8 100代入函数关系式即可；(2)静止即游速为零；(3)由鲑鱼A的游速大于鲑鱼B的游速，可列出不等式，解该不等式即可．‎ 解：(1)将x＝8 100代入函数关系式，得y＝log381＝×4＝2，所以一条鲑鱼的耗氧量是8 100个单位时，它的游速是‎2 m/s.‎ ‎(2)令y＝0，得log3＝0，即＝1，则x＝100，‎ 所以一条鲑鱼静止时耗氧量为100个单位．‎ ‎(3)由yA＞yB，得log3＞log3，即log3xA＞log3xB，‎ 则xA＞xB，所以鲑鱼A的耗氧量较大． ‎ 迁移与应用　解：(1)由题意知，当燕子静止时，它的速度v＝0，‎ 可得0＝5log2，解得Q＝10，‎ 即燕子静止时的耗氧量是10个单位．‎ ‎(2)将耗氧量Q＝80代入所给公式，得 v＝5log2＝5log28＝15(m/s)，‎ 即当一只燕子的耗氧量是80个单位时，它的飞行速度为‎15 m/s.‎ ‎【当堂检测】‎ ‎1．A　解析：由图像是一条射线知其所对应的函数模型是一次函数模型．‎ ‎2．D ‎3．B　解析：散点图如图所示：‎ 由散点图可知，此函数图像不是直线，排除A；此函数图像是上升的，是增函数，排除C，D，故选B.‎ ‎4．A　解析：设北冰洋冬季冰雪覆盖面积每年为上一年的q%，则(q%)50＝0.95，∴q%＝，‎ 即x年后湖水量为y＝·m.‎ ‎5．　解析：由题意知面积S＝(3＋x)＝－＋＋6，‎ 当x＝－＝时，面积S最大．‎