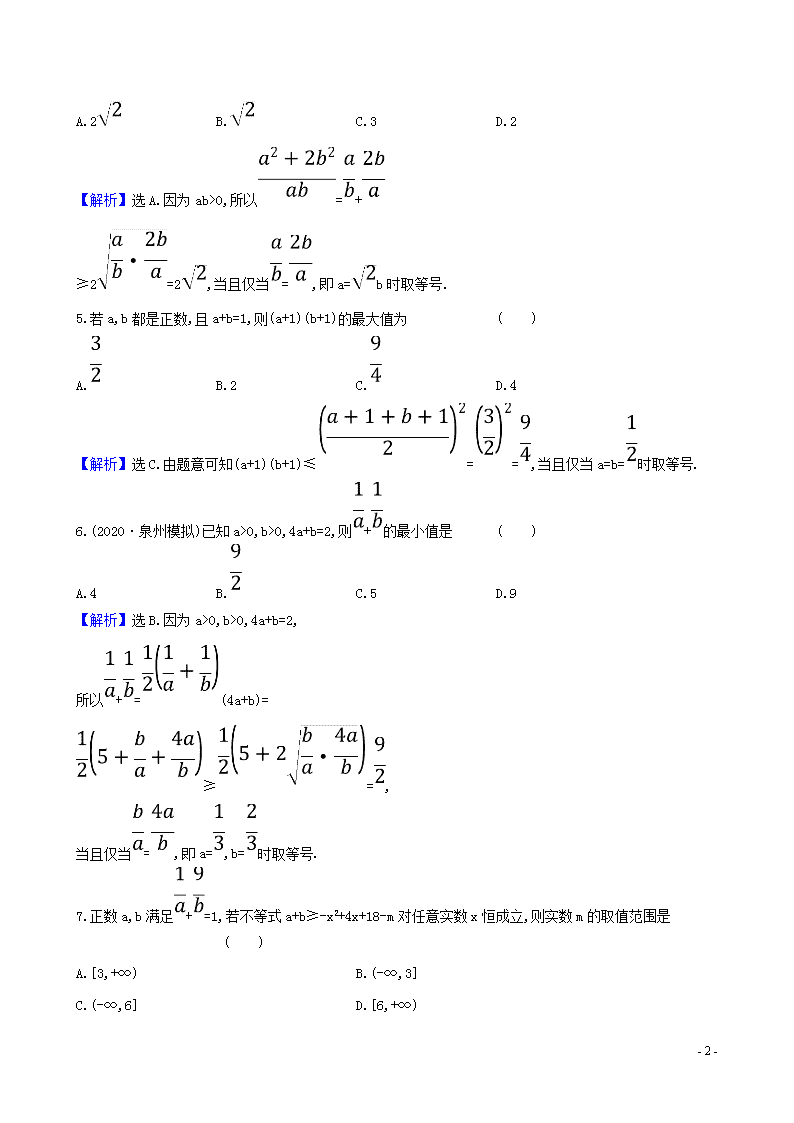2021版高考数学一轮复习核心素养测评三十一基本不等式理北师大版 7页

核心素养测评三十一 基本不等式 ‎(25分钟　50分)‎ 一、选择题(每小题5分,共35分)‎ ‎1.若a,b∈R,且ab>0,则下列不等式中,恒成立的是 (　　)‎ A.a+b≥2　 B.+>‎ C.+≥2　 D.a2+b2>2ab ‎【解析】选C.因为ab>0,所以>0,>0,所以+≥2=2,当且仅当a=b时取等号.‎ ‎2.(2020·宿州模拟)已知函数y=x-4+(x>-1),当x=a时,y取得最小值b,则2a+3b等于 (　　)‎ A.9　 B.7　 C.5　　 D.3‎ ‎【解析】选B.因为x>-1,所以x+1>0,‎ 所以y=x-4+=x+1+-5≥‎ ‎2-5=1,当且仅当x+1=,即x=2时取等号,‎ 所以y取得最小值b=1,此时x=a=2,所以2a+3b=7.‎ ‎3.若log2x+log2y=1,则2x+y的最小值为 (　　)‎ A.1 B.2 C.2 D.4‎ ‎【解析】选D.因为log2x+log2y=1,所以log2xy=1,所以xy=2,‎ 所以2x+y≥2=4,当且仅当2x=y,即x=1,y=2时取等号.所以2x+y的最小值为4.‎ ‎4.(2019·温州模拟)若ab>0,则的最小值为(　　)‎ - 7 -‎ A.2 B. C.3 D.2‎ ‎【解析】选A.因为ab>0,所以=+‎ ‎≥2=2,当且仅当=,即a=b时取等号.‎ ‎5.若a,b都是正数,且a+b=1,则(a+1)(b+1)的最大值为 (　　)‎ A.　 B.2　 C.　 D.4‎ ‎【解析】选C.由题意可知(a+1)(b+1)≤==,当且仅当a=b=时取等号.‎ ‎6.(2020·泉州模拟)已知a>0,b>0,4a+b=2,则+的最小值是 (　　)‎ A.4　　 B.　　 C.5　　　 D.9‎ ‎【解析】选B.因为a>0,b>0,4a+b=2,‎ 所以+=(4a+b)=‎ ‎≥=,‎ 当且仅当=,即a=,b=时取等号.‎ ‎7.正数a,b满足+=1,若不等式a+b≥-x2+4x+18-m对任意实数x恒成立,则实数m的取值范围是 (　　)‎ A.[3,+∞)　 B.(-∞,3]‎ C.(-∞,6]　 D.[6,+∞)‎ - 7 -‎ ‎【解析】选D.因为a>0,b>0,+=1,‎ 所以a+b=(a+b)=10++≥10+2=16,当且仅当=,即a=4,b=12时,等号成立.由题意,得16≥-x2+4x+18-m,‎ 即x2-4x-2≥-m对任意实数x恒成立,‎ 令f(x)=x2-4x-2,‎ 则f(x)=x2-4x-2=(x-2)2-6,‎ 所以f(x)的最小值为-6,‎ 所以-6≥-m,即m≥6.‎ 二、填空题(每小题5分,共15分)‎ ‎8.某公司购买一批机器投入生产,据市场分析,每台机器生产的产品可获得的总利润y(单位:万元)与机器运转时间x(单位:年)的关系式为y=-x2+18x-25(x∈N*),则当每台机器运转________________年时,年平均利润最大,最大值是________________万元. ‎ ‎【解析】每台机器运转x年的年平均利润为=18-,而x>0,故≤18-2=8,当且仅当x=5时等号成立,此时年平均利润最大,最大值为8万元.‎ 答案:5　8‎ ‎9.已知x,y为正实数,则+的最小值为________________. ‎ ‎【解析】因为x,y为正实数,则+‎ ‎=++1=++1,‎ - 7 -‎ 令t=,则t>0,所以+=+t+1=+t++≥2+=,当且仅当t=时取等号.‎ 所以+的最小值为.‎ 答案:‎ ‎10.(2019·阳泉模拟)函数y=(x<1)的最大值为________________.  ‎ ‎【解析】函数y==‎ ‎=x+1+=(x-1)++2 (x<1),‎ 因为(1-x)+≥2,当且仅当x=0时,取等号,‎ 所以(x-1)+≤-2,当且仅当x=0时,取等号.‎ 故函数y=的最大值为0.‎ 答案:0‎ ‎(15分钟　25分)‎ ‎1.(5分)设a>0,b>0,则下列不等式中不成立的是 (　　)‎ A.a+b+≥2‎ - 7 -‎ B.≥‎ C.≥a+b D.(a+b)≥4‎ ‎【解析】选B.因为a>0,b>0,‎ 所以a+b+≥2+≥2,当且仅当a=b且2=,即a=b=时取等号,故A成立;‎ 因为a+b≥2>0,所以≤,‎ 当且仅当a=b时取等号,‎ 所以≥不一定成立,故B不成立,‎ 因为≤=,当且仅当a=b时取等号,‎ ‎=‎ ‎=a+b-≥2-,当且仅当a=b时取等号,‎ 所以≥,所以≥a+b,‎ 故C一定成立,因为(a+b)=2++≥4,‎ 当且仅当a=b时取等号,故D一定成立.‎ ‎2.(5分)当00)有公共点的圆称之为C的“望圆”,则曲线C的所有“望圆”中半径最小值为 (　　)‎ A.4　　 B.　 C.8　　 D.2‎ ‎【解析】选D.根据题意,设为曲线C上任意一点,“望圆”的半径为r,若“望圆”与曲线C有公共点,则r2=(t+1)2+=t2++2+2≥2+2×2+2=8,当且仅当t=时,等号成立,则r的最小值为2.‎ ‎4.(5分)(2019·赣州模拟)已知正数x,y满足x+y=5,则+的最小值为________________.  ‎ ‎【解析】正数x,y满足x+y=5,所以(x+1)+(y+2)=8,‎ 则+=[(x+1)+(y+2)]‎ ‎=≥‎ ‎=,‎ - 7 -‎ 当且仅当x+1=y+2,即x=3,y=2时,上式取得最小值.‎ 答案:‎ ‎5.(5分)(2020·朝阳模拟)在△ABC中,内角A,B,C的对边分别为a,b,c,若a2+b2+ab=c2,且△ABC的面积为c,则ab的最小值为________________. ‎ ‎【解析】在△ABC中,a2+b2+ab=c2,结合余弦定理a2+b2-2abcos C=c2,‎ 可得cos C=- ,所以sin C=.‎ 由三角形面积公式,可得c=absin C代入化简可得c=,‎ 代入a2+b2+ab=c2中可得a2+b2=-ab,‎ 因为a2+b2≥2ab,所以-ab≥2ab,解不等式可得ab≥48,‎ 所以ab的最小值为48.‎ 答案:48‎ - 7 -‎