河北省邢台市2020届高三联考数学（文）试卷 13页

文科数学试卷 注意事项：‎ ‎1、答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。‎ ‎2、回答选择题时，选出每小题答案后，用 2B 铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。‎ ‎3、考试结束后，将本试卷和答题卡一并交回。‎ 一、选择题：本题共 12 小题，每小题 5 分，共 60 分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．已知集合 M = {x Î Z | -1 £ x £ 1}, N = {x Î Z | x(x - 2) £ 0} ，则 M Ç N = ( )‎ A．{-1,2}‎ ‎B.{0,1}‎ ‎C.{-1,0,1}‎ ‎D.{-1,0,1,2}‎ 2. 若 z = 3 + 4i + iz （ i 是虚数单位），则 z = （ ）‎ ‎1- i ‎3 5‎ A． B．2 C．‎ ‎2 2‎ ‎‎ D．3‎ ® ® ® ® ® ® ® ® 3. 已知向量 a ，b 满足 a = 2 ， b = 1 且 a+ b = 2 ，则 a 与 b 夹角的余弦值为（ ）‎ ‎2‎ ‎2‎ ‎2‎ ‎2‎ A． B． C． D．‎ ‎2 3 8 4‎ 4. 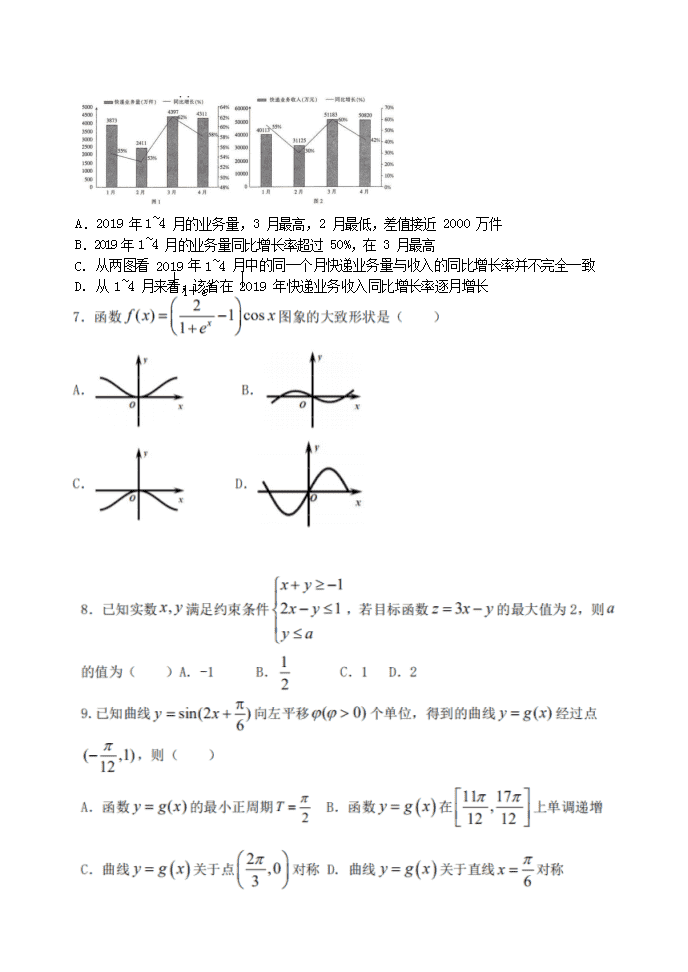已知数列{an }是公比不为 1 的等比数列， sn 为其前 n 项和，满足a2 = 2 ，且 ‎16a1 ,9a4 ,2a7 成等差数列，则 s3 = （ ）‎ A．5 B．6 C．7 D．9‎ A．2019 年 1~4 月的业务量，3 月最高，2 月最低，差值接近 2000 万件B．2019 年 1~4 月的业务量同比增长率超过 50%，在 3 月最高 C. 从两图看 2019 年 1~4 月中的同一个月快递业务量与收入的同比增长率并不完全一致 D. 从 1~4 月来看，该省在 2019 年快递业务收入同比增长率逐月增长 ç 1+ ex ÷ ‎10.在棱长为 1 的正方体 ABCD - A1B1C1D1 中， E, F 分别为线段CD 和 A1B1 上的动点 且满足CE = A1F ，则四边形 D1FBE 所围成的图形（如图所示阴影部分）分别在该正方体有公共顶点的三个面上的正投影的面积之和（ ）‎ ‎3‎ A. 有最小值 ‎2‎ ‎5‎ B. 有最大值 ‎2‎ ‎‎ C. 为定值 3 D．为定值 2‎ ‎11.斐波那契螺旋线，也称“黄金螺旋线”，是根据斐波那契数列 1，1，2，3，5，…画出来的螺旋曲线.如图，白色小圆内切于边长为 1 的正方形，黑色曲线就是斐波那契螺旋 线，它是依次在以 1，2，3，5 为边长的正方形中画一个圆心角为90o 的扇形，将其圆弧连接起来得到的.若在矩形 ABCD 内随机取一点，则此点取自阴影部分的概率是（ ）‎ p A． B．‎ ‎4‎ ‎39p ‎160‎ ‎19p+1‎ C．‎ ‎80‎ ‎19p+ 2‎ D．‎ ‎80‎ 二、填空题：本题共 4 小题，每小题 5 分，共 20 分．‎ ‎13.某单位有 360 名职工，现采用系统抽样方法，抽取 20 人做问卷调查，将 360 人按 ‎1，2，…，360 随机编号，则抽取的 20 人中，编号落入区间[181, 288] 的人数为 ．‎ ‎14.已知圆C : (x - 3)2 + ( y -1)2 = 3 及直线l : ax + y - 2a - 2 = 0 ，当直线l 被圆C 截得的弦长最短时，直线l 的方程为 .‎ ‎15.如图，矩形 ABCD 中， M 为 BC 的中点，将DABM 沿直线 AM 翻折成DAB1M ， 连结 B1D ， N 为 B1D 的中点，则在翻折过程中，下列说法中所有正确的序号是 .‎ ‎①存在某个位置，使得CN ^ AB ；‎ ‎②翻折过程中， CN 的长是定值；‎ ‎③若 AB = BM ，则 AM ^ B1D ；‎ ‎④若 AB = BM = 1 ，当三棱锥 B1 - AMD 的体积最大时，三棱锥 B1 - AMD 的外接球的表面积是 4p.‎ ‎16.在DABC 中，角 A, B, C 的对边分别为 a, b, c ，c = 4 ，a = 4 2 sin A ，且C 为锐角 ，则DABC 面积的最大值为 .‎ 三、解答题：共 70 分．解答应写出文字说明、证明过程或演算步骤．第 17~21 题为必考题，每个试题考生都必须作答．第 22，23 题为选考题，考生根据要求作答．‎ ‎（一）必考题：共 60 分．‎ ‎17．（12 分）已知等差数列{an } 的前 n 项和为 Sn ，若 S2 = 4 ， S5 = 25 ．‎ n n ‎（1）求数列{a }的通项公式；（2）记b = 1 ，求数列{b }的前 n 项和T ．‎ an+1a ‎n n n+2‎ ‎18．（12 分）如图，四边形 ABCD 为正方形， PD ^ 平面 ABCD ，点 E ， F 分别为 AD ， PC 的中点．‎ ‎PD = DC = 2 ，‎ ‎（Ⅰ）证明：‎ ‎DF / / 平面 PBE ；‎ ‎（Ⅱ）求点 F 到平面 PBE 的距离．‎ 城市 1‎ 城市 2‎ 城市 3‎ 城市 4‎ 城市 5‎ A 指标 ‎2‎ ‎4‎ ‎5‎ ‎6‎ ‎8‎ B 指标 ‎3‎ ‎4‎ ‎4‎ ‎4‎ ‎5‎ ‎19．（12 分）近年来，共享单车在我国各城市迅猛发展，为人们的出行提供了便利，但也给城市的交通管理带来了一些困难，为掌握共享单车在C 省的发展情况，某调查机构从该省抽取了 5 个城市，并统计了共享单车的 A 指标 x 和 B 指标 y ，数据如下表所示：‎ （1） 试求 y 与 x 间的相关系数 r ，并说明 y 与 x 是否具有较强的线性相关关系（若 ‎| r |³ 0.75 ，则认为 y 与 x 具有较强的线性相关关系，否则认为没有较强的线性相关关系）.‎ （2） 建立 y 关于 x 的回归方程，并预测当 A 指标为 7 时， B 指标的估计值.‎ （3） 若某城市的共享单车 A 指标 x 在区间( x - 3s, x + 3s) 的右侧，则认为该城市共享单车数量过多，对城市的交通管理有较大的影响交通管理部门将进行治理，直至 A 指标 x 在区间( x - 3s, x + 3s) 内现已知C 省某城市共享单车的 A 指标为 13，则该城市的交通管理部门是否需要进行治理？试说明理由.‎ 参考公式：回归直线 y = bx + a 中斜率和截距的最小二乘估计分别为 文科数学参考答案 一、 选择题 ‎1—5：BCDCD 6—10：DBCCD 11—12：DC 二、 填空题 ‎13：6 14： 15：②④ 16：‎ 三、 解答题 ‎17：（1）设等差数列的首项为，公差为，因为 ，，‎ 则：，解得，‎ 所以．---------------------------------------------------------------------（6分）‎ ‎（2）由于，‎ 所以．‎ 则．-------（12分）‎ ‎18：（Ⅰ）证明：取点是的中点，连接， ，则，且，‎ ‎∵且，‎ ‎∴且，‎ ‎∴四边形为平行四边形，‎ ‎∴，∴平面．----------（6分）‎ ‎（Ⅱ）解：由（Ⅰ）知平面，所以点到平面的距离与到平面的距离是相等的，故转化为求点到平面的距离，设为．‎ 利用等体积法： ，即， ，‎ ‎∵， ，∴，∴．--------------------（12分）‎ ‎19：（1）由题得，‎ 所以，，‎ 则.‎ 因为，所以与具有较强的线性相关关系.-------------------------------------（5分）‎ ‎（2）由（1）得，，‎ 所以线性回归方程为.------------------------------------------------------------（8分）‎ 当时，，‎ 即当指标为7时，指标的估计值为4.6.--------------------------------------------------（10分）‎ ‎（3）由题得，‎ 因为，所以该城市的交通管理部门需要进行治理.----------------------------------（12分）‎ ‎20：（1）直线的一般方程为.‎ 依题意，解得，故椭圆的方程式为.--------（4分）‎ ‎（2）假若存在这样的直线，‎ 当斜率不存在时，以为直径的圆显然不经过椭圆的左顶点，‎ 所以可设直线的斜率为，则直线的方程为.‎ 由，得.‎ 由，得.‎ 记，的坐标分别为，，‎ 则，，‎ 而 .---------------------------------（8分）‎ 要使以为直径的圆过椭圆的左顶点，则，‎ 即 ，‎ 所以 ，‎ 整理解得或，‎ 所以存在过的直线，使与椭圆交于，两点，且以为直径的圆过椭圆的左顶点，直线的方程为或.-------------------------------（12分）‎ ‎21：（1）函数的定义域为，，‎ 令，则，，‎ ‎（i）若，则恒成立，所以在上是增函数，------------（2分）‎ ‎（ii）若，则，‎ 当时，，是增函数，‎ 当时，，是减函数，‎ 当时，，是增函数，-----------------------------------------（4分）‎ ‎（iii）若，则，‎ 当时，，是增函数，‎ 当时，，是减函数，‎ 当时，，是增函数 综上所述：当时，在上是增函数，‎ 当，在上是增函数，在上是减函数，在上是增函数，‎ 当时，在上是增函数，在上是减函数，在上是增函数；‎ ‎--------------------------------------------------------------------------------------------------------（6分）‎ ‎（2）当时，‎ 在上是增函数，在上是减函数，在上是增函数，‎ 所以的极小值为，‎ 的极大值为,‎ 设，其中，‎ ‎,‎ 所以在上是增函数，‎ 所以，‎ 因为，‎ 所以有且仅有1个，使.‎ 所以当时，有且仅有1个零点.------------------------------------------（12分）‎ ‎22：（1）曲线，，‎ 曲线的直角坐标方程为，即，‎ 直线的参数方程为：（为参数），‎ 直线的普通方程为：----------------------------------------------（5分）‎ ‎（2）直线的参数方程为：（为参数），‎ 代入，得，‎ ‎，‎ ‎．---------------------------------（10分）‎ ‎23：（I）因为，所以. ‎ ‎① 当时，得，解得，所以; ‎ ‎② 当时，得，解得，所以;‎ ‎③ 当时，得，解得，所以; ‎ 综上所述，实数的取值范围是 ------------------------------------------------（6分）‎ ‎（II） ，因为,‎ 所以 -----------------------------------------------（10分）‎