江苏省淮安市六校联盟2020届高三第三次学情调查数学（文）试题 16页

‎2019-2020学年江苏省淮安市六校联盟高三第三次学情调查数学试卷（文科）‎ 一、填空题（本大题共14小题，每小题5分，共计70分）‎ ‎1．已知集合A＝{﹣3，﹣1，1，2}，集合B＝[0，+∞），则A∩B＝　 　．‎ ‎2．若复数z＝（1+i）（3﹣ai）（i为虚数单位）为纯虚数，则实数a＝　 　．‎ ‎3．函数y＝的定义域为　 　．‎ ‎4．“x＞‎2”‎是“x2+3x﹣4＞‎0”‎的　 　条件．（从“充要”，“充分不必要”，“必要不充分”，“既不充分又不必要”中选择一个正确的填写）‎ ‎5．已知等差数列{an}，a4+a6＝10，前5项的和S5＝5，则其公差为　 　．‎ ‎6．已知 f（x）是定义在R上的奇函数，当 x＜0时f（x）＝log2（2﹣x），则f（0）+f（2）＝　 　．‎ ‎7．在平面直角坐标系xOy中，若中心在坐标原点的双曲线的一条准线方程为，且它的一个顶点与抛物线y2＝﹣4x的焦点重合，则该双曲线的渐近线方程为　 　．‎ ‎8．如图所示，长方体ABCD﹣A1B‎1C1D1的体积为36，E为线段B‎1C上的一点，则棱锥A﹣DED1的体积为　 　．‎ ‎9．若曲线C1：y＝ax3﹣6x2+12x与曲线C2：y＝ex在x＝1处的两条切线互相垂直，则实数a的值为　 　．‎ ‎10．已知正实数x，y满足xy﹣x﹣2y＝1，则x+2y的最小值为　 　．‎ ‎11．已知菱形ABCD的边长为2，∠BAD＝120°，点E、F分别在边BC、DC上，＝λ，＝μ．若＝1，•＝﹣，则λ+μ＝　 　．‎ ‎12．已知点A（﹣1，0），B（2，0），直线l：kx﹣y﹣5k＝0上存在点P，使得PA2+2PB2＝9成立，则实数k的取值范围是　 　．‎ ‎13．在三角形ABC中，角A、B、C、所对的边分别为a、b、c，若b＝3，2sin‎2A+sin2B+‎ C，则sinC的最大值是　 　．‎ ‎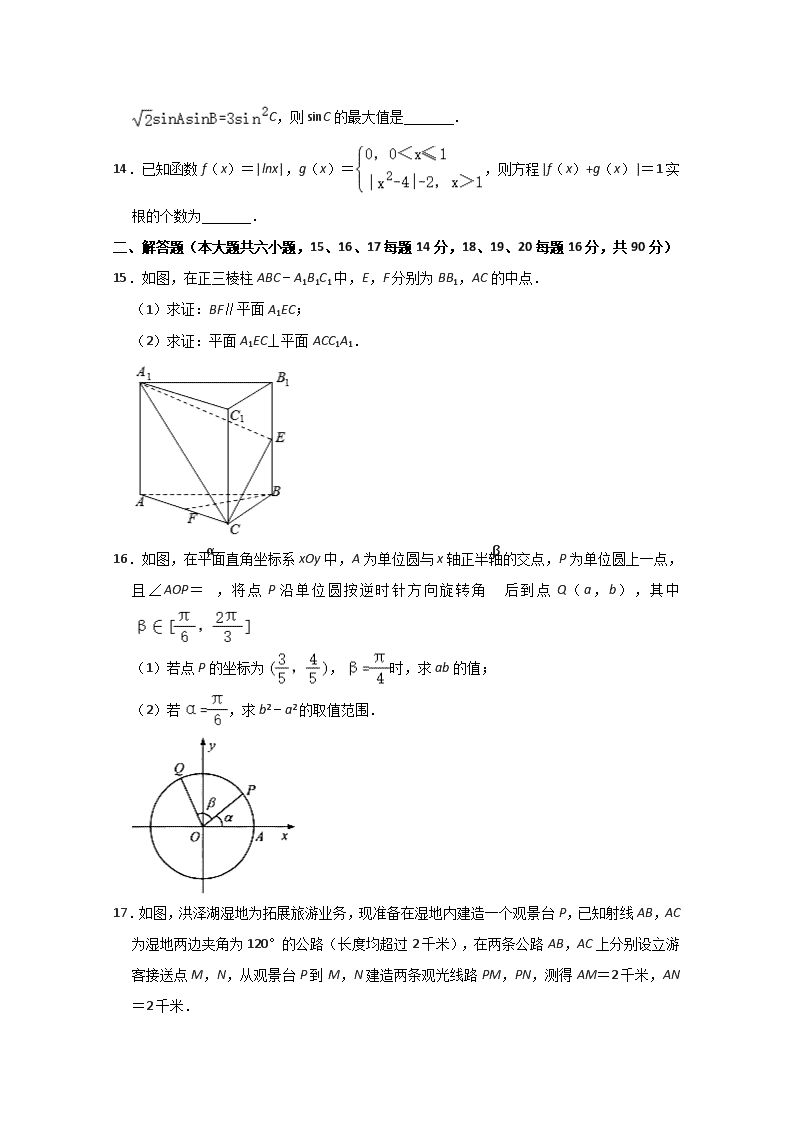14．已知函数f（x）＝|lnx|，g（x）＝，则方程|f（x）+g（x）|＝1实根的个数为　 　．‎ 二、解答题（本大题共六小题，15、16、17每题14分，18、19、20每题16分，共90分）‎ ‎15．如图，在正三棱柱ABC﹣A1B‎1C1中，E，F分别为BB1，AC的中点．‎ ‎（1）求证：BF∥平面A1EC；‎ ‎（2）求证：平面A1EC⊥平面ACC‎1A1．‎ ‎16．如图，在平面直角坐标系xOy中，A为单位圆与x轴正半轴的交点，P为单位圆上一点，且∠AOP＝α，将点P沿单位圆按逆时针方向旋转角β后到点Q（a，b），其中 ‎（1）若点P的坐标为，时，求ab的值；‎ ‎（2）若，求b2﹣a2的取值范围．‎ ‎17．如图，洪泽湖湿地为拓展旅游业务，现准备在湿地内建造一个观景台P，已知射线AB，AC为湿地两边夹角为120°的公路（长度均超过‎2千米），在两条公路AB，AC上分别设立游客接送点M，N，从观景台P到M，N建造两条观光线路PM，PN，测得AM＝‎2千米，AN＝‎2千米．‎ ‎（1）求线段MN的长度；‎ ‎（2）若∠MPN＝60°，求两条观光线路PM与PN之和的最大值．‎ ‎18．（16分）在平面直角坐标系xOy中，已知椭圆C：+＝1（a＞b＞0）的左、右焦点分别为F1、F2，焦距为2，一条准线方程为x＝2．P为椭圆C上一点，直线PF1交椭圆C于另一点Q．‎ ‎（1）求椭圆C的方程；‎ ‎（2）若点P的坐标为（0，b），求过P、Q、F2三点的圆的方程；‎ ‎（3）若＝λ，且λ∈（，2），求•的最大值．‎ ‎19．（16分）已知数列{an}和{bn}满足：a1＝λ，an+1＝+n﹣4，bn＝（﹣1）n（an﹣3n+21），其中λ为实数，n为正整数．‎ ‎（1）对任意实数λ，证明：数列{an}不是等比数列；‎ ‎（2）证明：当λ≠18时，数列 {bn} 是等比数列；‎ ‎（3）设Sn为数列 {bn} 的前n项和，是否存在实数λ，使得对任意正整数n，都有Sn＞﹣12？若存在，求λ的取值范围；若不存在，说明理由．‎ ‎20．（16分）已知函数f（x）＝lnx﹣ax2+x，a∈R．‎ ‎（1）若a＝2，求函数f（x）的单调区间；‎ ‎（2）若关于x的不等式f（x）≤ax﹣1恒成立，求整数a的最小值．‎ ‎（3）若a＝﹣2，正实数x1，x2满足f（x1）+f（x2）+x1x2＝0，证明：x1+x2≥．‎ ‎2019-2020学年江苏省淮安市六校联盟高三（上）第三次学情调查数学试卷（文科）（12月份）‎ 参考答案与试题解析 一、填空题（本大题共14小题，每小题5分，共计70分）‎ ‎1．已知集合A＝{﹣3，﹣1，1，2}，集合B＝[0，+∞），则A∩B＝　{1，2}　．‎ ‎【解答】解：∵A＝{﹣3，﹣1，1，2}，B＝[0，+∞），‎ ‎∴A∩B＝{1，2}，‎ 故答案为：{1，2}．‎ ‎2．若复数z＝（1+i）（3﹣ai）（i为虚数单位）为纯虚数，则实数a＝　﹣3　．‎ ‎【解答】解：复数z＝（1+i）（3﹣ai）＝3+a+（3﹣a）i，‎ ‎∵复数z为纯虚数，‎ ‎∴，解得a＝﹣3．‎ 故答案为：﹣3．‎ ‎3．函数y＝的定义域为　[2，+∞）　．‎ ‎【解答】解：由2x﹣4≥0，得2x≥4，则x≥2．‎ ‎∴函数y＝的定义域为[2，+∞）．‎ 故答案为：[2，+∞）．‎ ‎4．“x＞‎2”‎是“x2+3x﹣4＞‎0”‎的　充分　条件．（从“充要”，“充分不必要”，“必要不充分”，“既不充分又不必要”中选择一个正确的填写）‎ ‎【解答】解：x2+3x﹣4＞0，‎ 解得：x＞1或x＜﹣4．‎ ‎∴x＞‎2”‎是“x2+3x﹣4＞‎0”‎的充分不必要条件．‎ 故答案为：充分．‎ ‎5．已知等差数列{an}，a4+a6＝10，前5项的和S5＝5，则其公差为　2　．‎ ‎【解答】解：∵等差数列{an}，a4+a6＝10，前5项的和S5＝5，设公差为d．‎ 由题意可得 ‎2a1+8d＝10，‎5a1+＝5，‎ 解方程组求得d＝2，‎ 故答案为 2．‎ ‎6．已知 f（x）是定义在R上的奇函数，当 x＜0时f（x）＝log2（2﹣x），则f（0）+f（2）＝　﹣2　．‎ ‎【解答】解：f（x）是定义在R上的奇函数，当 x＜0时f（x）＝log2（2﹣x），‎ 则f（0）+f（2）＝0﹣f（﹣2）＝﹣log2（2+2）＝﹣2，‎ 故答案为：﹣2．‎ ‎7．在平面直角坐标系xOy中，若中心在坐标原点的双曲线的一条准线方程为，且它的一个顶点与抛物线y2＝﹣4x的焦点重合，则该双曲线的渐近线方程为　y＝x　．‎ ‎【解答】解：设双曲线的方程为，‎ ‎∵抛物线y2＝﹣4x中2p＝4‎ ‎∴抛物线y2＝﹣4x的焦点F（﹣1，0），‎ ‎∵双曲线的一个顶点与抛物线y2＝﹣4x的焦点重合 ‎∴a＝1，‎ 又∵双曲线的一条准线方程为，‎ ‎∴，解得c＝2，‎ ‎∴b2＝4﹣1＝3，即 ‎∴双曲线的渐近线方程为y＝x，‎ 故答案为：y＝x．‎ ‎8．如图所示，长方体ABCD﹣A1B‎1C1D1的体积为36，E为线段B‎1C上的一点，则棱锥A﹣DED1的体积为　1　．‎ ‎【解答】解：∵长方体ABCD﹣A1B‎1C1D1的体积为36，E为线段B‎1C上的一点，‎ ‎∴棱锥A﹣DED1的体积为：‎ ‎＝＝＝1．‎ 故答案为：1．‎ ‎9．若曲线C1：y＝ax3﹣6x2+12x与曲线C2：y＝ex在x＝1处的两条切线互相垂直，则实数a的值为　﹣　．‎ ‎【解答】解：由y＝ax3﹣6x2+12x，得y′＝3ax2﹣12x+12，‎ ‎∴y′|x＝1＝‎3a，‎ 由y＝ex，得y′＝ex，‎ ‎∴y′|x＝1＝e．‎ ‎∵曲线C1：y＝ax3﹣6x2+12x与曲线C2：y＝ex在x＝1处的切线互相垂直，‎ ‎∴‎3a•e＝﹣1，解得：a＝﹣．‎ 故答案为：﹣．‎ ‎10．已知正实数x，y满足xy﹣x﹣2y＝1，则x+2y的最小值为　4+2　．‎ ‎【解答】解：正实数x，y满足xy﹣x﹣2y＝1，xy＝x+2y+1，‎ 由基本不等式可得，xy＝x•（2y），当且仅当x＝2y时取等号，‎ ‎∴x+2y+1，‎ ‎∵x+2y＞0‎ 解不等式可得，x+2y 故答案为：4+2‎ ‎11．已知菱形ABCD的边长为2，∠BAD＝120°，点E、F分别在边BC、DC上，＝λ，＝μ．若＝1，•＝﹣，则λ+μ＝　　．‎ ‎【解答】解：由题意可得若•＝（+）•（+），‎ ‎＝•+•+•+• ‎ ‎＝2×2×cos120°+•μ+λ•+λ•μ ‎＝﹣2+4μ+4λ+λμ×2×2×cos120°‎ ‎＝4λ+4μ﹣2λμ﹣2＝1，‎ ‎∴4λ+4μ﹣2λμ＝3 ①．‎ ‎•＝﹣•（﹣）＝•＝（1﹣λ）•（1﹣μ）‎ ‎＝（1﹣λ）•（1﹣μ）‎ ‎＝（1﹣λ）（1﹣μ）×2×2×cos120°＝（1﹣λ﹣μ+λμ）（﹣2）＝﹣，‎ 即﹣λ﹣μ+λμ＝﹣②．‎ 由①②求得λ+μ＝，‎ 故答案为：．‎ ‎12．已知点A（﹣1，0），B（2，0），直线l：kx﹣y﹣5k＝0上存在点P，使得PA2+2PB2＝9成立，则实数k的取值范围是　[]　．‎ ‎【解答】解：由题意得：直线l：y＝k（x﹣5），‎ 因此直线l经过定点（5，0）；‎ 设点P坐标为（x0，y0）；∵PA2+2PB2＝9，‎ ‎∴‎ 化简得：，‎ 因此点p为x2+y2﹣2x＝0与直线l：y＝k（x﹣5）的交点．‎ 所以应当满足圆心（1，0）到直线的距离小于等于半径 ‎∴‎ 解得：‎ 故答案为 ‎13．在三角形ABC中，角A、B、C、所对的边分别为a、b、c，若b＝3，2sin‎2A+sin2B+‎ C，则sinC的最大值是　　．‎ ‎【解答】解：∵b＝3，2sin‎2A+sin2B+C，‎ ‎∴由正弦定理可得：‎2a2+b2+ab＝‎3c2，可得c2＝，‎ 所以cosC＝＝＝≥＝，当且仅当a＝b＝3时取等号，‎ 故sinCmax＝＝．‎ 故答案为：．‎ ‎14．已知函数f（x）＝|lnx|，g（x）＝，则方程|f（x）+g（x）|＝1实根的个数为　4　．‎ ‎【解答】解：由|f（x）+g（x）|＝1可得g（x）＝﹣f（x）±1．‎ g（x）与h（x）＝﹣f（x）+1的图象如图所示，图象有2个交点 g（x）与φ（x）＝﹣f（x）﹣1的图象如图所示，图象有两个交点；‎ 所以方程|f（x）+g（x）|＝1实根的个数为4．‎ 故答案为：4．‎ 二、解答题（本大题共六小题，15、16、17每题14分，18、19、20每题16分，共90分）‎ ‎15．如图，在正三棱柱ABC﹣A1B‎1C1中，E，F分别为BB1，AC的中点．‎ ‎（1）求证：BF∥平面A1EC；‎ ‎（2）求证：平面A1EC⊥平面ACC‎1A1．‎ ‎【解答】证明：（1）连接A‎1C与AC1交于点O，连接OF，‎ ‎∵F为AC的中点，‎ ‎∴OF∥C‎1C且OF＝C‎1C，‎ ‎∵E为BB1的中点，‎ ‎∴BE∥C‎1C且BE＝C‎1C，‎ ‎∴BE∥OF且BE＝OF，‎ ‎∴四边形BEOF是平行四边形，‎ ‎∴BF∥OE，‎ ‎∵BF⊄平面A1EC，OE⊂平面A1EC，‎ ‎∴BF∥平面A1EC ‎（2）∵AB＝CB，F为AC的中点，‎ ‎∴BF⊥AC 由（1）知BF∥OE，‎ ‎∴OE⊥AC，‎ ‎∵AA1⊥底面ABC，BF⊂底面ABC，‎ ‎∴AA1⊥BF，‎ ‎∵BF∥OE，‎ ‎∴OE⊥AA1，‎ ‎∵AA1∩AC＝A，‎ ‎∴OE⊥平面AA‎1C1C ‎∵OE⊂面A1EC，‎ ‎∴平面A1EC⊥平面AA‎1C1C．‎ ‎16．如图，在平面直角坐标系xOy中，A为单位圆与x轴正半轴的交点，P为单位圆上一点，且∠AOP＝α，将点P沿单位圆按逆时针方向旋转角β后到点Q（a，b），其中 ‎（1）若点P的坐标为，时，求ab的值；‎ ‎（2）若，求b2﹣a2的取值范围．‎ ‎【解答】解：（1）A为单位圆与x轴正半轴的交点，P为单位圆上一点，‎ 且∠AOP＝α，将点P沿单位圆按逆时针方向旋转角β后到点Q（a，b），其中，‎ 若点P的坐标为，时，‎ 则cosα＝，sinα＝，且a＝cos（α+），b＝sin（α+），‎ 故ab＝sin（α+）cos（α+）＝sin（2α+）＝cos2α＝（2cos2α﹣1）＝﹣．‎ ‎（2）若，则a＝cos（β+），b＝sin（β+），‎ ‎∴b2﹣a2 ＝﹣＝﹣cos（2β+）．‎ ‎∵，∴2β+∈[，]，∴cos（2β+）∈[﹣1，]，‎ ‎∴b2﹣a2 ＝﹣cos（2β+）∈[﹣，1]．‎ ‎17．如图，洪泽湖湿地为拓展旅游业务，现准备在湿地内建造一个观景台P，已知射线AB，AC为湿地两边夹角为120°的公路（长度均超过‎2千米），在两条公路AB，AC上分别设立游客接送点M，N，从观景台P到M，N建造两条观光线路PM，PN，测得AM＝‎2千米，AN＝‎2千米．‎ ‎（1）求线段MN的长度；‎ ‎（2）若∠MPN＝60°，求两条观光线路PM与PN之和的最大值．‎ ‎【解答】解：（1）在△AMN中，由余弦定理得，MN2＝AM2+AN2﹣2AM•ANcos120°…‎ ‎＝，‎ 所以千米． …‎ ‎（2）设∠PMN＝α，因为∠MPN＝60°，所以∠PNM＝120°﹣α 在△PMN中，由正弦定理得，．…‎ 因为＝，‎ 所以PM＝4sin（1200﹣α），PN＝4sinα…‎ 因此PM+PN＝4sin（1200﹣α）+4sinα…‎ ‎＝‎ ‎＝＝…‎ 因为0°＜α＜120°，所以30°＜α+30°＜150°．‎ 所以当α+300＝900，即α＝600时，PM+PN取到最大值．…‎ 答：两条观光线路距离之和的最大值为千米．…（16分）‎ ‎18．（16分）在平面直角坐标系xOy中，已知椭圆C：+＝1（a＞b＞0）的左、右焦点分别为F1、F2，焦距为2，一条准线方程为x＝2．P为椭圆C上一点，直线PF1交椭圆C于另一点Q．‎ ‎（1）求椭圆C的方程；‎ ‎（2）若点P的坐标为（0，b），求过P、Q、F2三点的圆的方程；‎ ‎（3）若＝λ，且λ∈（，2），求•的最大值．‎ ‎【解答】解：（1）由题意可得，解得c＝1，a2＝2，‎ ‎∴b2＝a2﹣c2＝1，‎ ‎∴椭圆C的方程为；‎ ‎（2）∵P（0，1），F1（﹣1，0），‎ ‎∴直线PF1的方程为x﹣y+1＝0，‎ 由，解得，或，‎ ‎∴点Q的坐标为（﹣，﹣），‎ 设过P，Q，F2三点的圆的方程为x2+y2+Dx+Ey+F＝0，‎ ‎∴，解得，‎ ‎∴所求圆的方程为x2+y2+；‎ ‎（3）设P（x1，y1），Q（x2，y2），‎ 则＝（x1+1，y1），＝（﹣1﹣x2，﹣y2 ），‎ ‎∵＝λ，‎ ‎∴，即，‎ ‎∴，解得x2＝，‎ ‎∴＝x1x2+y1y2‎ ‎＝x2（﹣1﹣λ﹣λx2）﹣‎ ‎＝﹣‎ ‎＝﹣‎ ‎＝，‎ ‎∵，‎ ‎∴，当且仅当，即λ＝1时取等号，‎ ‎∴，‎ 即的最大值为．‎ ‎19．（16分）已知数列{an}和{bn}满足：a1＝λ，an+1＝+n﹣4，bn＝（﹣1）n（an﹣3n+21），其中λ为实数，n为正整数．‎ ‎（1）对任意实数λ，证明：数列{an}不是等比数列；‎ ‎（2）证明：当λ≠18时，数列 {bn} 是等比数列；‎ ‎（3）设Sn为数列 {bn} 的前n项和，是否存在实数λ，使得对任意正整数n，都有Sn＞﹣12？若存在，求λ的取值范围；若不存在，说明理由．‎ ‎【解答】解：（1）证明：假设存在一个实数λ，使{an}是等比数列，则有a22＝a‎1a3，‎ 即（）2＝2，矛盾．‎ 所以{an}不是等比数列．‎ ‎（2）解：因为bn+1＝（﹣1）n+1[an+1﹣3（n+1）+21]＝（﹣1）n+1（an﹣2n+14）‎ ‎＝﹣（﹣1）n•（an﹣3n+21）＝﹣bn 当λ≠﹣18时，b1＝﹣（λ+18）≠0，由上可知bn≠0，∴（n∈N+）．‎ 故当λ≠﹣18时，数列{bn}是以﹣（λ+18）为首项，﹣为公比的等比数列 ‎（3）当λ＝﹣18时，bn＝0，从而Sn＝0．成立．‎ 当λ≠﹣18时，由（Ⅱ）得，于是，‎ 要使对任意正整数n，都有Sn＞﹣12．‎ 即．‎ 令 当n为正奇数时，‎ 当n为正偶数时，，∴．（16分）‎ 于是可得．‎ 综上所述，存在实数λ，使得对任意正整数n，都有Sn＞﹣12；λ的取值范围为（﹣∞，﹣6）．（18分）‎ ‎20．（16分）已知函数f（x）＝lnx﹣ax2+x，a∈R．‎ ‎（1）若a＝2，求函数f（x）的单调区间；‎ ‎（2）若关于x的不等式f（x）≤ax﹣1恒成立，求整数a的最小值．‎ ‎（3）若a＝﹣2，正实数x1，x2满足f（x1）+f（x2）+x1x2＝0，证明：x1+x2≥．‎ ‎【解答】解：（1）若a＝2，则f（x）＝lnx﹣x2+x，（x＞0），‎ f′（x）＝﹣2x+1＝﹣，‎ f′（x）＜0可得2x2﹣x﹣1＞0，又x＞0，解得x＞1，‎ 即有f（x）的减区间为（1，+∞），增区间为（0，1）；‎ ‎（2）f（x）≤ax﹣1恒成立，可得lnx﹣ax2+x﹣ax+1≤0恒成立，‎ 令g（x）＝lnx﹣ax2+x﹣ax+1，g′（x）═，‎ ‎①当a≤0时，∵x＞0，∴﹣ax2+（1﹣a）x+1＞0，∴g′（x）＞0‎ g（x）在（0，+∞）单调递增，且g（1）＝﹣，‎ 此时不等式f（x）≤ax﹣1不恒成立．‎ ‎②当a＞0时，g．‎ 当）时，g′（x）＞0，x时，g′（x）＜0‎ ‎∴g（x）在（0，）递增，在（）d递减，‎ 故g（x）max＝g（）＝‎ 令h（a）＝，（a＞0），显然函数h（a）在（0，+∞）递减．‎ 且h（1）＝．‎ ‎∴整数a的最小值为2．‎ ‎（3）证明：由f（x1）+f（x2）+x1x2＝0，‎ 即lnx1+x12+x1+lnx2+x22+x2+x1x2＝0，‎ 从而（x1+x2）2+（x1+x2）＝x1x2﹣ln（x1x2），‎ 令t＝x1x2，则由φ（t）＝t﹣lnt，‎ 由x1＞0，x2＞0，即x1+x2＞0．‎ φ′（t）＝．t＞0‎ 可知，φ（t）在区间（0，1）上单调递减，在区间（1，+∞）上单调递增．‎ 所以φ（t）≥φ（1）＝1，‎ 所以（x1+x2）2+（x1+x2）≥1，解得：x1+x2≥．或x1+x．‎ 因为x1＞0，x2＞0，‎ 因此x1+x2≥成立．‎