思想03 数形结合思想（文）02（测试卷）-2017年高考数学二轮复习精品资料（新课标版） 14页

思想三 数形结合思想 强化训练2‎ 一、选择题 ‎1.【广东省汕头市2017届高三上学期期末】假设你家订了一份牛奶，奶哥在早上6：00~7：00之间随机地把牛奶送到你家，而你在早上6：30~7：30之间随机第离家上学，则你在理考家前能收到牛奶的概率是（ ）‎ A． B． C. D．‎ ‎【答案】D ‎2. 【中原名校豫南九校2017届第四次质量考评】已知某几何体的三视图（单位：）如图所示，则该几何体的表面积是（ ）‎ A． B． C. D．‎ ‎【答案】C ‎【解析】如图所示，该几何体是棱长为2的正方体砍去两个小三棱柱得到的四棱柱，其表面积.选C.‎ ‎3. 【河南省豫北名校联盟2017届高三年级精英对抗赛】已知实数满足不等式组，若目标函数的最大值不超过4，则实数的取值范围是（ ）‎ A． B． C. D．‎ ‎【答案】D ‎4. 【广东省汕头市2017届高三上学期期末，12】在平面内，定点满足，，动点满足，，则的最大值是（ ）‎ A． B． C. 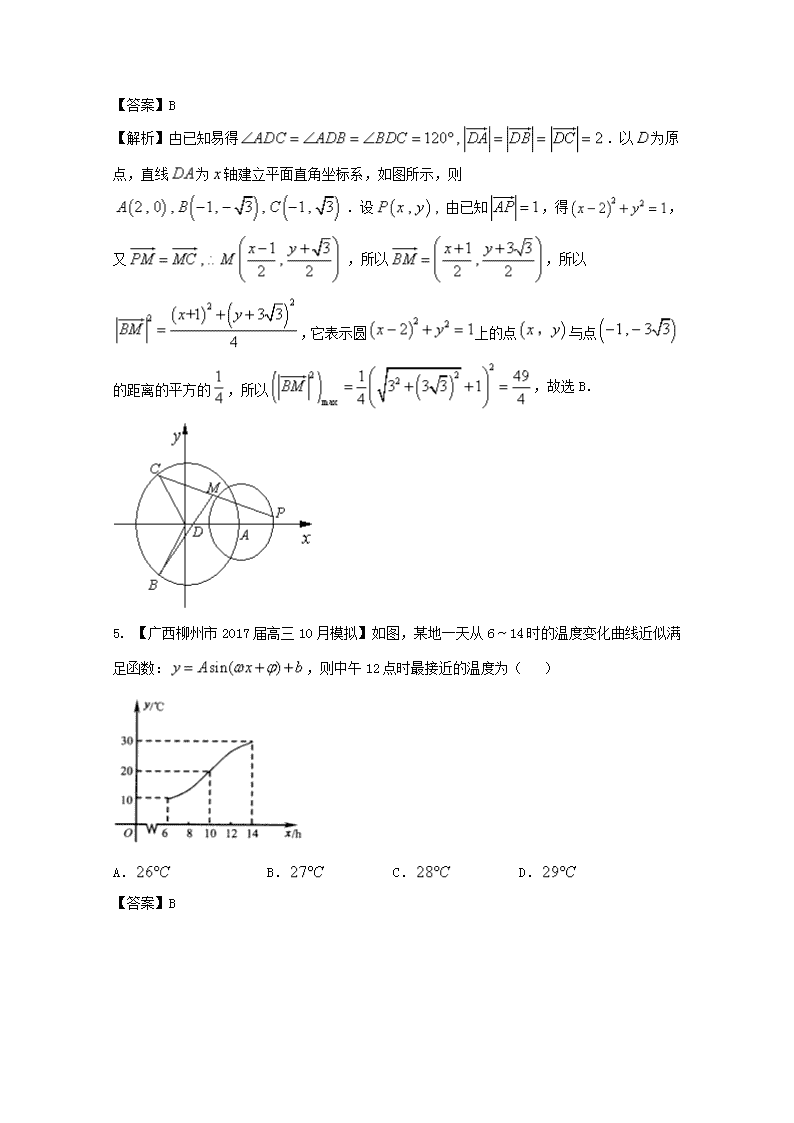D．‎ ‎【答案】B ‎【解析】甴已知易得．以为原点，直线为轴建立平面直角坐标系，如图所示，则．设由已知，得，又，所以，所以，它表示圆上的点与点的距离的平方的，所以，故选B．‎ ‎5. 【广西柳州市2017届高三10月模拟】如图，某地一天从614时的温度变化曲线近似满足函数：，则中午12点时最接近的温度为（ ）‎ A． B． C． D．‎ ‎【答案】B ‎6. 【河南省广东省佛山市2017届高三教学质量检测（一），12】已知函数，（是常数），若在上单调递减，则下列结论中：‎ ‎①；②；③有最小值.‎ 正确结论的个数为（ ）‎ A．0 B．1 C.2 D．3‎ ‎【答案】C ‎【解析】‎ 试题分析：由题意，得，若函数在上单调递减，则，即，所以，故②正确；不妨设，则，故①错；画出不等式组表示的平面区域，如图所示，令，则，①当，即时，抛物线与直线有公共点，联立两个方程消去得，，所以；当，即时，抛物线与平面区域必有公共点，综上所述，，所以有最小值，故③正确，故选C．‎ ‎7. 【2017届广东省珠海市高三上学期期末】在直角梯形中，，分别为的中点，以为圆心，为半径的圆弧中点为(如图所示).若，其中，则的值是（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】以为原点，为轴，为轴建立平面直角坐标系，则，，，，，∵，∴，∴，解得：，则，故选B.‎ ‎8. 【重庆市第八中学2017届高三上学期第二次适应性考试】已知函数若当方程有四个不等实根，，，‎ ‎（）时，不等式恒成立，则实数的最小值为（ ）‎ A． B． C． D．‎ ‎【答案】B ‎【解析】当时，，所以，由此画出函数的图象如下图所示，由于，故.且.所以，，由分离参数得，，令，则上式化为，即，此方程有实数根，判别式大于或等于零，即，解得，所以，故选B.‎ ‎9. 【福建省福州外国语学校2017届高三适应性考试（三）】已知函数，，当时，方程根的个数是（ ）‎ A．8 B．6 C．4 D．2‎ ‎【答案】B ‎10. 【安徽师范大学附属中学2017届高三上学期期中考查】已知正方体，则下列说法不正确的是（ ）‎ A.若点在直线上运动时，三棱锥的体积不变 B.若点是平面上到点和距离相等的点，则点的轨迹是过点的直线 C.若点在直线上运动时，直线与平面所成角的大小不变 D.若点在直线上运动时，二面角的大小不变 ‎【答案】C ‎【解析】试题分析：A选项中，由正方体的性质可得：,于是平面,因此直线上的点到平面的距离不变，点在直线上运动时，的面积不变，因此三棱锥的体积不变；B选项中，设正方体的棱长为，以为坐标原点，建立空间直角坐标系，则，由可得，整理可得，所以点的轨迹是过点的直线，故B正确；当点在直线上运动时，由A可知：直线上的点到平面 的距离不变，而的大小在改变，因此直线与平面所成角的大小会随点的移动而变化，故C错误；D选项中，当点在直线上运动时，由A可知：直线上的点到平面的距离不变，到的距离不变，因此二面角的大小不变，故D正确，故选C.‎ 二、填空题 ‎11. 【河南省豫北名校联盟2017届高三上学期精英对抗赛】已知圆:，若直线上至少存在一点，使得以该点为圆心，1为半径的圆与圆有公共点，则实数的取值范围为 ．‎ ‎【答案】‎ ‎【解析】配方得，直线过，画出图像如下图所示，由图可知，原命题“直线上至少存在一点，使得以该点为圆心，为半径的圆与圆有公共点”等价于“圆心到直线的距离不大于”，即，解得.‎ ‎12. 【河北省冀州中学2017届高三（复习班）上学期第二次阶段考试】函数在上的部分图象如图所示，则 的值为_____.‎ ‎【答案】‎ ‎13. 【2017届湖南省衡阳市高三上学期期末】表面积为的球面上有四点，且是边长为的等边三角形，若平面平面，则三棱锥体积的最大值是__________．‎ ‎【答案】‎ ‎【解析】∵，故当到面的距离最大时，三棱锥的体积最大，由图可知即当，为中点时，三棱锥的体积最大，作，面，连接，由，得，由于，得，故，，故，，， ，故答案为.‎ ‎14.【2017届江西省上饶市高三第一次模拟】已知在中，，，如图，动点 是在以点为圆心，为半径的扇形内运动（含边界）且；设，则的取值范围__________．‎ ‎【答案】‎ ‎【解析】由已知图形可知的夹角，所以，‎ 的夹角，所以，由平行四边形法则可知当点沿着圆弧由到移动时，负数逐渐增大，正数逐渐增大，所以当点在处时取得最小值，，，当点在处时取得最大值，，，所以的取值范围为.‎ 三、解答题 ‎15. 【湖南省五市十校教研教改共同体2017届高三12月联考】已知分别为三个内角的对边，且．‎ ‎（1）求；‎ ‎（2）若为边上的中线，，求的面积．‎ ‎16.【天津六校2017届高三上学期期中联考】如图，四棱锥中，平面，为线段上一点，为的中点．‎ ‎（1）证明：；‎ ‎（2）求四面体的体积．‎ ‎【解析】（1）由已知得，取的中点，连接，由为中点知，即，又，即，故四边形为平行四边形，于是，因为平面平面，所以平面. ‎ ‎17. 【2017届江西省上饶市高三第一次模拟】已知椭圆：，圆：的圆心在椭圆上，点到椭圆的右焦点的距离为2．‎ ‎（1）求椭圆的方程；‎ ‎（2）过点作直线交椭圆于，两点，若，求直线的方程．‎ ‎【解析】（1）因为椭圆的右焦点，，所以，因为在椭圆上，所以，‎ 由，得，，所以椭圆的方程为．‎ ‎（2）由得：，即，可得 ‎，‎ ‎①当垂直轴时，，此时满足题意，所以此时直线的方程为；‎ ‎②当不垂直轴时，设直线的方程为，由消去得，‎ 设，，所以，，代入可得：，‎ 代入，，得，代入化简得：，解得，‎ 经检验满足题意，则直线的方程为，综上所述直线的方程为或．‎ ‎ ‎