2018届二轮复习 坐标系与参数方程 课件理（全国通用） 30页

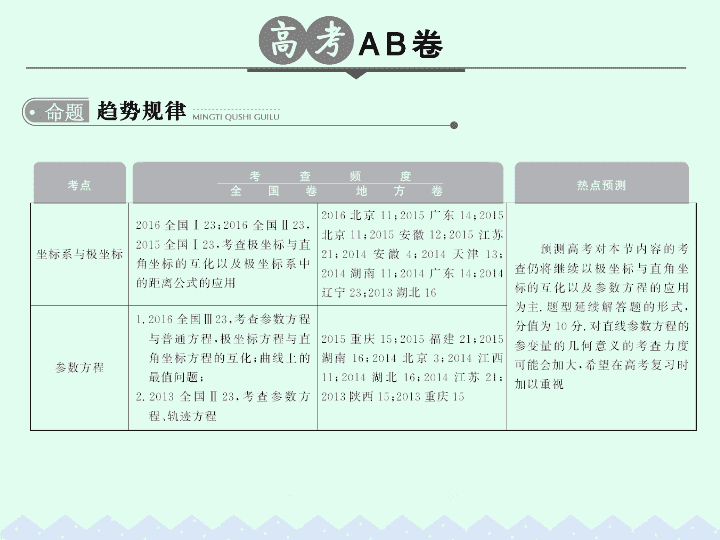
知识点一 极坐标与直角坐标 1. 极坐标系的概念 (1) 在平面内取一个定点 O ，叫作极点；自极点 O 引一条射线 Ox ，叫作极轴；再选定一个 单位、一个 单位 ( 通常取弧度 ) 及其 ( 通常取逆时针方向 ) ，这样就建立了一个极坐标系 . 长度 角度 正方向 (2) 设 M 是平面内一点，极点 O 与点 M 的距离 | OM | 叫作点 M 的极径，记为 ρ ；以极轴 Ox 为始边，射线 OM 为终边的角 xOM 叫作点 M 的极角，记为 θ ，有序数对 ( ρ ， θ ) 叫作点 M 的极坐标，记为 ( ρ ， θ ). 2. 极坐标与直角坐标的互化 ρ cos θ ρ sin θ x 2 ＋ y 2 3. 圆的极坐标方程 (1) 圆心在极点，半径为 R 的圆的极坐标方程为 ρ ＝ R . (2) 圆心在极轴上的点 ( a ， 0) 处，且过极点 O 的圆的极坐标方程为 ρ ＝ 2 a cos θ . (3) 圆心在点处，且过极点 O 的圆的极坐标方程为 ρ ＝ 2 a sin θ . ► 三个前提条件：极坐标与直角坐标互化的前提条件 . (1) [ ① 极点与原点重合； ② 极轴与 x 轴正方向重合； ③ 取相同的单位长度 ] 若曲线的极坐标方程为 ρ ＝ 2sin θ ＋ 4cos θ ，以极点为原点，极轴为 x 轴正半轴建立直角坐标系，则该曲线的直角坐标方程为 ________. 解析　 ∵ ρ ＝ 2sin θ ＋ 4cos θ ， ∴ ρ 2 ＝ 2 ρ sin θ ＋ 4 ρ cos θ ， ∴ x 2 ＋ y 2 ＝ 2 y ＋ 4 x ， 即 x 2 ＋ y 2 － 2 y － 4 x ＝ 0. 答案 　 x 2 ＋ y 2 － 4 x － 2 y ＝ 0 ► 两个易错点 ， 忽略点的极坐标不唯一性和变量范围致误 . (2) [ 在由点的直角坐标化为极坐标时 ， 要注意点所在的象限和极角的范围 ， 否则点的极坐标将不唯一 ] 点 M 的直角坐标为 ( －，－ 1) ，则其极坐标为 ________. (3) [ 在曲线的方程进行互化时 ， 要注意变量的范围 ， 注意转化的等价性 ] 极坐标方程 ( ρ － 1)( θ －π ) ＝ 0( ρ ≥ 0) 表示的图形是 ________( 填序号 ). ① 两个圆； ② 两条直线； ③ 一个圆和一条射线； ④ 一条直线和一条射线 . 解析　 由 ( ρ － 1)( θ －π ) ＝ 0( ρ ≥ 0) 得 ， ρ ＝ 1 或 θ ＝π . 其中 ρ ＝ 1 表示以极点为圆心 ， 半径为 1 的圆 ， θ ＝π表示以极点为起点与 Ox 反向的射线 . 答案 　 ③ ► 一类极坐标方程：直线的极坐标方程 . 答案 　 2 知识点 二 参数方程 1. 常见的参数方程 2. 参数方程与普通方程的互化 (1) 化参数方程为普通方程 消去参数方程中的参数，就可把参数方程化为普通方程，消去参数的常用方法有： ① 代入消元法； ② 加减消元法； ③ 乘除消元法； ④ 三角恒等式消元法 . ► 一个易错点：忽略直线方程的标准形式致误 . 答案 　 ( － 3 ， 6) 或 (5 ，－ 2) ► 四个结论：常用的四个消参结论 . 极坐标系与极坐标方程的应用突破方略 (1) 极坐标方程与直角坐标方程互化的思路 ① 对于简单的问题可直接代入公式 ρ cos θ ＝ x ， ρ sin θ ＝ y ， ρ 2 ＝ x 2 ＋ y 2 ，但有时需要作适当变化，如将式子两边平方或两边同乘 ρ 等 . ② 如果要判断曲线的形状，则可以将方程化为直角坐标方程后再进行判断 . (2) 求解与极坐标有关的问题的主要方法 ① 直接利用极坐标系求解，求解时可与数形结合思想结合使用； ② 转化为直角坐标系后，用直角坐标求解 . 使用后一种时应注意，若结果要求的是极坐标，还应将直角坐标化为极坐标 . 答案 　 D [ 点评 ] 　 在极坐标系中研究曲线的形状、性质时 ，最常用的方法是化极坐标方程为直角坐标方程，转化为熟悉的问题，对一些简单的直线或圆的有关问题，也可以直接用极坐标知识解决 . 解决参数方程问题要熟练掌握直线、圆、圆锥曲线的参数方程的建立过程，特别是要明晰直线的参数方程中参数的几何意义，熟练掌握参数方程与普通方程互化的常见方法，学会在互化中寻找解题方案、优化解题思路 . 参数方程的应用求解策略 (1) 求直线 l 的倾斜角； (2) 若直线 l 与曲线 C 交于 A ， B 两点，求 | AB |.  极坐标、参数方程的综合应用 (1) 写出圆 C 的标准方程和直线 l 的参数方程； (2) 设直线 l 与圆 C 相交于 A ， B 两点，求 | PA |·| PB | 的值 . [ 规律方法 ] 　 (1) 涉及参数方程和极坐标方程的综合题 ， 求解的一般方法是分别化为普通方程和直角坐标方程后求解 . 当然 ， 还要结合题目本身特点 ， 确定选择何种方程 . (2) 数形结合的应用 ， 即充分利用参数方程中参数的几何意义 ， 或者利用 ρ 和 θ 的几何意义 ， 直接求解 ， 能达到化繁为简的解题目的 .