2019高三数学文北师大版一轮课时分层训练21+正弦定理和余弦定理 9页

课时分层训练(二十一)　 正弦定理和余弦定理 (对应学生用书第 208 页) A 组　基础达标 (建议用时：30 分钟) 一、选择题 1．(2018·兰州模拟)设△ABC 的内角 A，B，C 所对的边分别为 a，b，c，若 bcos C＋ccos B＝asin A，则△ABC 的形状为(　　) A．锐角三角形 B．直角三角形 C．钝角三角形 D．不确定 B　[由正弦定理得 sin Bcos C＋sin Ccos B＝sin2A， ∴sin(B＋C)＝sin2A， 即 sin(π－A)＝sin2A，sin A＝sin2A． ∵A∈(0，π)，∴sin A＞0，∴sin A＝1，即 A＝π 2.] 2．在△ABC 中，已知 b＝40，c＝20，C＝60°，则此三角形的解的情况是(　　) A．有一解 B．有两解 C．无解 D．有解但解的个数不确定 C　[由正弦定理得 b sin B ＝ c sin C ， ∴sin B＝bsin C c ＝ 40 × 3 2 20 ＝ 3＞1. ∴角 B 不存在，即满足条件的三角形不存在．] 3．(2016·天津高考)在△ABC 中，若 AB＝ 13，BC＝3，∠C＝120°，则 AC＝ (　　) A．1　　　　 B．2　　　　 C．3　　　　 D．4 A　[由余弦定理得 AB 2 ＝AC 2 ＋BC 2 －2AC·BC·cos C，即 13＝AC 2 ＋9－ 2AC×3×cos 120°，化简得 AC2＋3AC－4＝0，解得 AC＝1 或 AC＝－4(舍去)．故 选 A．] 4．(2018·石家庄模拟)△ABC 中，AB＝ 3，AC＝1，∠B＝30°，则△ABC 的面积 等于(　　) 【导学号：00090111】 A． 3 2 B． 3 4 C． 3 2 或 3 D． 3 2 或 3 4 D　[由余弦定理得 AC2＝AB2＋BC2－2AB·BC·cos B， 即 1＝3＋BC2－3BC，解得 BC＝1 或 BC＝2， 当 BC＝1 时，△ABC 的面积 S＝1 2AB·BCsin B＝1 2 × 3×1×1 2 ＝ 3 4 . 当 BC＝2 时，△ABC 的面积 S＝1 2AB·BCsin B＝1 2 × 3×2×1 2 ＝ 3 2 . 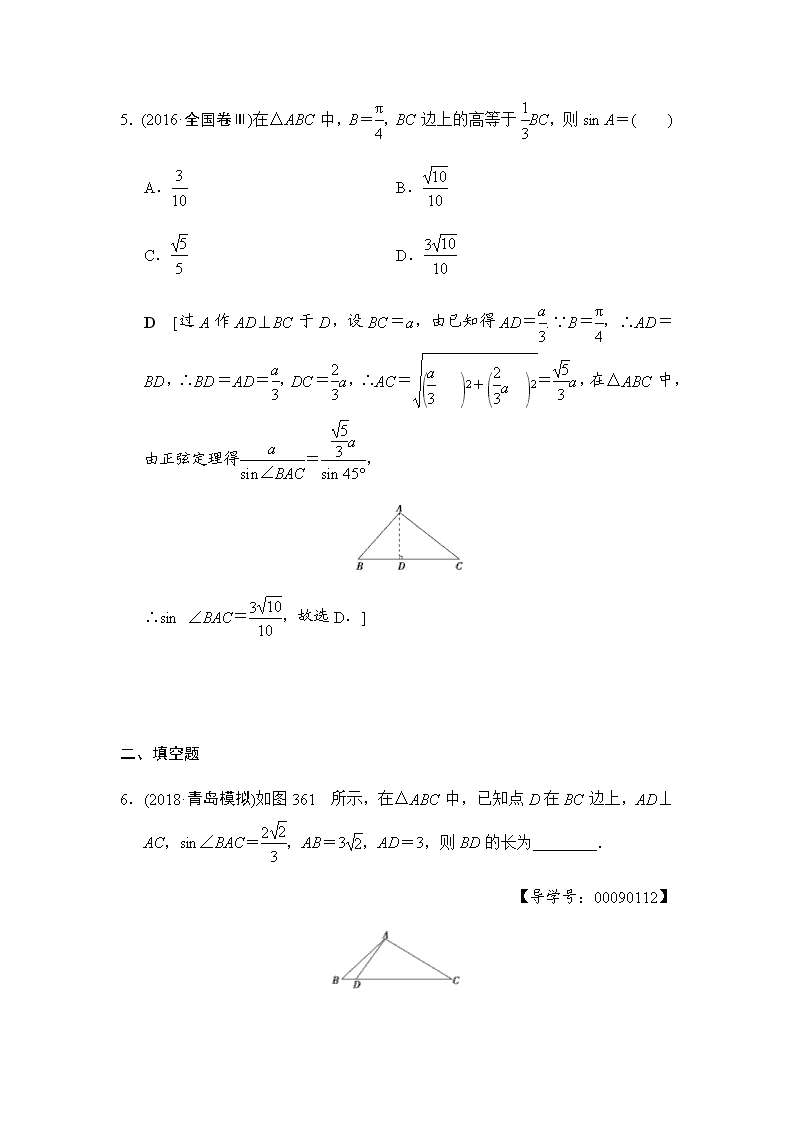总上之，△ABC 的面积等于 3 4 或 3 2 .] 5．(2016·全国卷Ⅲ)在△ABC 中，B＝π 4 ，BC 边上的高等于1 3BC，则 sin A＝(　　) A． 3 10 B． 10 10 C． 5 5 D．3 10 10 D　[过 A 作 AD⊥BC 于 D，设 BC＝a，由已知得 AD＝ a 3.∵B＝π 4 ，∴AD＝ BD，∴BD＝AD＝a 3 ，DC＝2 3a，∴AC＝ (a 3 )2＋(2 3a )2＝ 5 3 a，在△ABC 中， 由正弦定理得 a sin∠BAC ＝ 5 3 a sin 45° ， ∴sin ∠BAC＝3 10 10 ，故选 D．] 二、填空题 6．(2018·青岛模拟)如图 3­6­1 所示，在△ABC 中，已知点 D 在 BC 边上，AD⊥ AC，sin∠BAC＝2 2 3 ，AB＝3 2，AD＝3，则 BD 的长为________． 【导学号：00090112】 图 3­6­1 3　[∵sin∠BAC＝sin(90°＋∠BAD)＝cos∠BAD＝2 2 3 ， ∴在△ABD 中，有 BD2＝AB2＋AD－2AB·ADcos∠BAD， ∴BD2＝18＋9－2×3 2×3×2 2 3 ＝3， ∴BD＝ 3.] 7．已知△ABC 中，AB＝ 3，BC＝1，sin C＝ 3cos C，则△ABC 的面积为 ________． 3 2 　[由 sin C＝ 3cos C 得 tan C＝ 3＞0，所以 C＝π 3. 根据正弦定理可得 BC sin A ＝ AB sin C ，即 1 sin A ＝ 3 3 2 ＝2， 所以 sin A＝1 2.因为 AB＞BC，所以 A＜C，所以 A＝π 6 ，所以 B＝π 2 ，即三角形 为直角三角形， 故 S△ABC＝1 2 × 3×1＝ 3 2 .] 8．(2017·全国卷Ⅱ)△ABC 的内角 A，B，C 的对边分别为 a，b，c，若 2bcos B＝ acos C＋ccos A，则 B＝________. π 3 　[由 2bcos B＝acos C＋ccos A 及正弦定理， 得 2sin Bcos B＝sin Acos C＋sin Ccos A． ∴2sin Bcos B＝sin(A＋C)． 又 A＋B＋C＝π，∴A＋C＝π－B． ∴2sin Bcos B＝sin(π－B)＝sin B． 又 sin B≠0，∴cos B＝1 2.∴B＝π 3.] 三、解答题 9．(2018·陕西八校联考)已知△ABC 内接于单位圆，角 A，B，C 的对边分别为 a，b，c，且 2acos A＝ccos B＋bcos C． (1)求 cos A 的值； (2)若 b2＋c2＝4，求△ABC 的面积． [解]　(1)∵2acos A＝ccos B＋bcos C， ∴2sin A·cos A＝sin Ccos B＋sin Bcos C， 即 2sin A·cos A＝sin(B＋C)＝sin A． 4 分 又 0＜A＜π，∴sin A≠0. ∴2cos A＝1，cos A＝1 2. 6 分 (2)由(1)知 cos A＝1 2 ，∴sin A＝ 3 2 . ∵△ABC 内接于单位圆， a sin A ＝2R＝2，∴a＝2sin A＝ 3. 8 分 由 a2＝b2＋c2－2bccos A，得 bc＝b2＋c2－a2＝4－3＝1， 10 分 ∴S△ABC＝1 2bcsin A＝1 2 ×1× 3 2 ＝ 3 4 . 12 分 10．(2017·云南二次统一检测)△ABC 的内角 A，B，C 的对边分别为 a，b，c，m ＝(sin B,5sin A＋5sin C)与 n＝(5sin B－6sin C，sin C－sin A)垂直． (1)求 sin A 的值； (2)若 a＝2 2，求△ABC 的面积 S 的最大值． 【导学号：00090113】 [解]　(1)∵m＝(sin B,5sin A＋5sin C)与n＝(5sin B－6sin C，sin C－sin A)垂直， ∴m·n＝5sin2B－6sin Bsin C＋5sin2C－5sin2A＝0， 即 sin2B＋sin2C－sin2A＝6sin Bsin C 5 . 3 分 根据正弦定理得 b2＋c2－a2＝6bc 5 ， 由余弦定理得 cos A＝b2＋c2－a2 2bc ＝3 5. ∵A 是△ABC 的内角， ∴sin A＝ 1－cos2A＝4 5. 6 分 (2)由(1)知 b2＋c2－a2＝6bc 5 ， ∴6bc 5 ＝b2＋c2－a2≥2bc－a2. 8 分 又∵a＝2 2，∴bc≤10. ∵△ABC 的面积 S＝1 2bcsin A＝2bc 5 ≤4， ∴△ABC 的面积 S 的最大值为 4. 12 分 B 组　能力提升 (建议用时：15 分钟) 1．(2016·山东高考)△ABC 中，角 A，B，C 的对边分别是 a，b，c 已知 b＝c，a2 ＝2b2(1－sin A)，则 A＝(　　) A．3π 4 B．π 3 C．π 4 D．π 6 C　[∵b＝c，∴B＝C． 又由 A＋B＋C＝π 得 B＝π 2 －A 2. 由正弦定理及 a2＝2b2(1－sin A)得 sin2A＝2sin2B(1－sin A)， 即 sin2A＝2sin2(π 2 －A 2)(1－sin A)， 即 sin2A＝2cos2A 2(1－sin A)， 即 4sin2A 2cos2A 2 ＝2cos2A 2(1－sin A)， 整理得 cos2A 2(1－sin A－2sin2A 2)＝0， 即 cos2A 2(cos A－sin A)＝0. ∵0＜A＜π，∴0＜A 2 ＜π 2 ，∴cos A 2 ≠0， ∴cos A＝sin A．又 0＜A＜π，∴A＝π 4.] 2．如图 3­6­2，在△ABC 中，∠B＝45°，D 是 BC 边上的点，AD＝5，AC＝7，DC ＝3，则 AB 的长为________． 图 3­6­2 5 6 2 　[在△ADC 中，AD＝5，AC＝7，DC＝3， 由余弦定理得 cos ∠ADC＝AD2＋DC2－AC2 2AD·DC ＝－1 2 ， 所以∠ADC＝120°，∠ADB＝60°. 在△ABD 中，AD＝5，∠B＝45°，∠ADB＝60°， 由正弦定理得 AB sin ∠ADB ＝ AD sin B ， 所以 AB＝5 6 2 .] 3．(2018·昆明模拟)如图 3­6­3，在四边形 ABCD 中，∠DAB＝π 3 ，AD∶AB＝2∶ 3，BD＝ 7，AB⊥BC． 图 3­6­3 (1)求 sin∠ABD 的值； (2)若∠BCD＝2π 3 ，求 CD 的长. 【导学号：00090114】 [解]　(1)∵AD∶AB＝2∶3，∴可设 AD＝2k，AB＝3k. 又 BD＝ 7，∠DAB＝π 3 ， ∴由余弦定理，得( 7)2＝(3k)2＋(2k)2－2×3k×2kcosπ 3 ， 解得 k＝1，∴AD＝2，AB＝3， sin∠ABD＝ADsin∠DAB BD ＝ 2 × 3 2 7 ＝ 21 7 . (2)∵AB⊥BC，∴cos∠DBC＝sin∠ABD＝ 21 7 ， ∴sin∠DBC＝2 7 7 ，∴ BD sin∠BCD ＝ CD sin∠DBC ， ∴CD＝ 7 × 2 7 7 3 2 ＝4 3 3 .