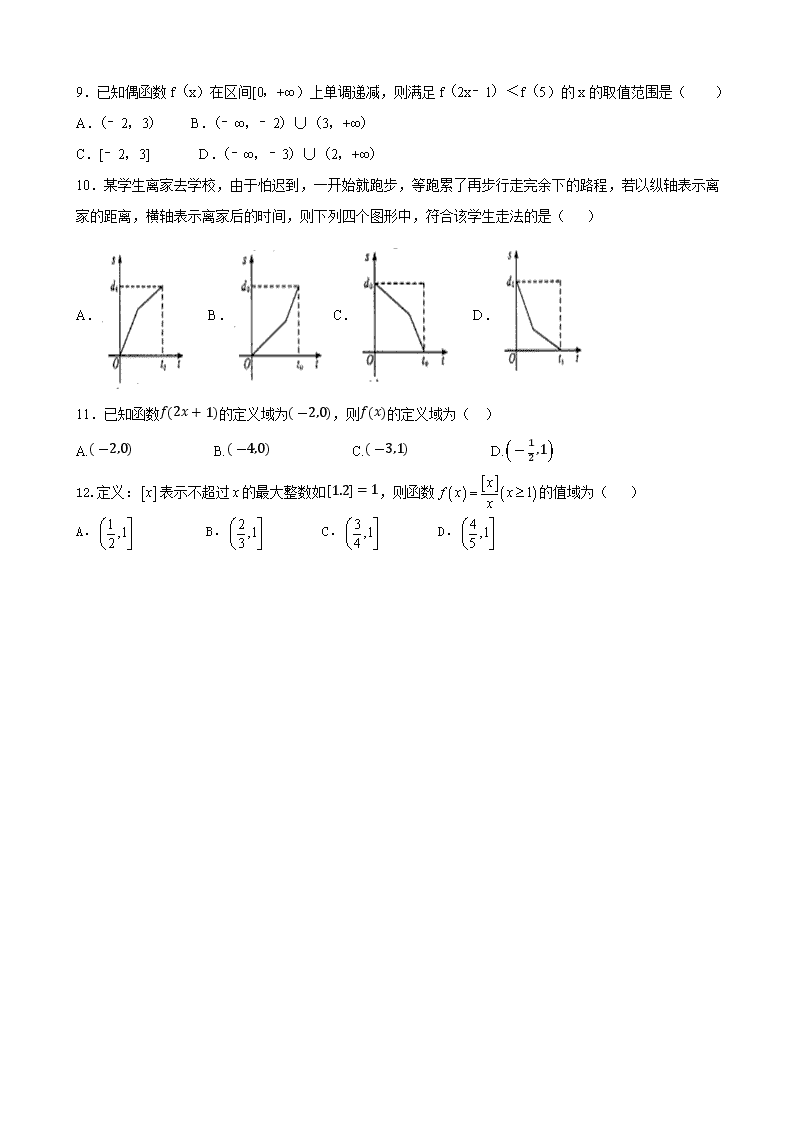2019-2020学年福建省华安一中、龙海二中高一上学期第一次联考试题 数学 5页

绝密★启用前 华安一中、龙海二中2019-2020学年上学期第一次月考 高一数学试题 ‎（考试时间：120分钟 总分：150分）‎ 一、选择题（本题共12个小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1．下列元素与集合的关系表示正确的是( )‎ ‎①N*；②∉Z；③∈Q；④π∈Q A．①② B．②③ C．①③ D．③④‎ ‎2.函数的定义域为（ ）‎ A． B． C． D． ‎ ‎3．已知函数f（x）=x‎2‎‎+1,(x≤0)‎‎-2x,(x>0)‎，则f（f（1））等于（　　）‎ A．3 B．4 C．5 D．6‎ ‎4．已知集合A={x|x＞1}，B={y|y=x2，x∈R}，则（　　）‎ A．A=B B．B‎⫋‎A C．A∩B=∅ D．A‎⫋‎B ‎5．函数的图像关于( )‎ A．y轴对称 B．直线y=x对称 C．直线y=-x对称 D．坐标原点对称 ‎6．下列哪组中的两个函数是同一函数 ( )‎ A．y=‎x+1‎‎2‎与y=‎x+1‎‎2‎ B．y=‎x‎4‎与y=‎x‎2‎ C．y=‎x‎2‎‎-1‎x-1‎与y=x+1‎ D．y=‎x与y=‎x‎2‎x ‎7．在下列由M到N的对应中构成映射的是　(　　)‎ A． B C D ‎8.若函数fx‎+1‎=x-‎x,则f（x）的解析式为（ ）‎ A．.fx=x‎2‎+3x+2‎ B.‎fx=x‎2‎-3x+2‎ C. .fx=x‎2‎+3x+2 (x≥1)‎ D. .fx=x‎2‎-3x+2 (x≥1)‎ ‎ ‎9．已知偶函数f（x）在区间[0，+∞）上单调递减，则满足f（2x﹣1）＜f（5）的x的取值范围是（　　）‎ A．（﹣2，3） B．（﹣∞，﹣2）∪（3，+∞）‎ C．[﹣2，3] D．（﹣∞，﹣3）∪（2，+∞）‎ ‎10．某学生离家去学校，由于怕迟到，一开始就跑步，等跑累了再步行走完余下的路程，若以纵轴表示离家的距离，横轴表示离家后的时间，则下列四个图形中，符合该学生走法的是（ ） ‎ A． B． C． D．‎ ‎11．已知函数f‎2x+1‎的定义域为‎-2,0‎，则fx的定义域为（ ）‎ A.‎-2,0‎ B.‎-4,0‎ C.‎-3,1‎ D.‎‎-‎1‎‎2‎,1‎ ‎12.定义：表示不超过的最大整数如‎1.2‎‎=1‎，则函数的值域为（ ）‎ A． B． C． D．‎ 二、填空题（本大题共4小题，每小题5分，共20分）‎ ‎13．集合A={－1，0，1}，B={a+1，2a}，若A∩B={0}，则实数a的值为________。‎ ‎14．函数（，）的图象恒过定点，则点的坐标为__________.‎ ‎15．定义在上的奇函数满足：当，则 ．‎ ‎16. 若函数在上为增函数，则取值范围为 .‎ 三、解答题（本题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤）‎ ‎17．计算：(1) ‎（‎9‎‎4‎‎）‎‎1‎‎2‎-‎-2.5‎‎0‎-‎8‎‎27‎‎2‎‎3‎+‎‎3‎‎2‎‎-2‎；‎ ‎(2) 已知.求： ；‎ ‎18．已知集合，或．‎ ‎（1）若，求；‎ ‎（2）若，求实数的取值范围.‎ ‎19．设a>0，且a≠1，函数y＝a2x＋2ax－1在[－1，1]上的最大值是14，则实数a的值 ‎20．已知函数，若在区间[2，3]上有最大值1.‎ ‎（1）求的值；‎ ‎（2）若在[2,4]上单调，求实数的取值范围.‎ ‎21.（12分）已知函数 ‎ ‎（1）求的值.‎ ‎（2）设求g(x)的值域.‎ ‎22．（本小题12分）已知函数y＝x＋有如下性质：如果常数t＞0，那么该函数在(0，]上是减函数，在[，＋∞)上是增函数．‎ ‎(1)已知f(x)＝x‎2‎‎-8x+4‎x，x∈[1,3]，利用上述性质，求函数f(x)的单调区间和值域；‎ ‎(2)对于(1)中的函数f(x)和函数g(x)＝－x－2a，若对任意x1∈[1,3]，总存在x2∈[0,1]，使得g(x2)＝f(x1)成立，求实数a的值．‎ 华安一中、龙海二中2019-2020学年上学期第一次月考 高一数学试题（参考答案）‎ 一、选择题：‎ BCCDD BCDBA CA 二. 填空题：‎ ‎（13）-1 （14）(1,2) （15） -3 （16）[1,2]‎ 三、解答题：‎ ‎17.(1)‎1‎‎2‎ (2) 11‎ ‎18.解：解：（1） ‎ ‎ （2）的取值范围为（1,3） ‎ ‎19.3 或‎1‎‎3‎ ‎20.（1）-1‎ ‎（2）（‎‎-∞，-6‎‎∪‎-2，+∞‎）‎ ‎21.（1）3.5‎ ‎ （2）‎‎1，+∞‎ ‎22．解　(1)y＝f(x)＝x‎2‎‎-8x+4‎x‎=x+‎4‎x-8‎，x∈[1,3]， ‎ 由已知性质得，当1≤x≤2时，f(x)单调递减， ‎ 当2≤x≤3时，f(x)单调递增， ‎ f(x)的值域为[－4，－3]．‎ ‎(2)g(x)＝－x－2a为减函数，‎ 故g(x)∈[－1－2a，－2a]，x∈[0,1]．‎ 由题意，f(x)的值域是g(x)的值域的子集，‎ ‎∴，∴a＝.‎