高中数学选修2-1公开课课件2_3_2双曲线的简单几何性质(二) 13页

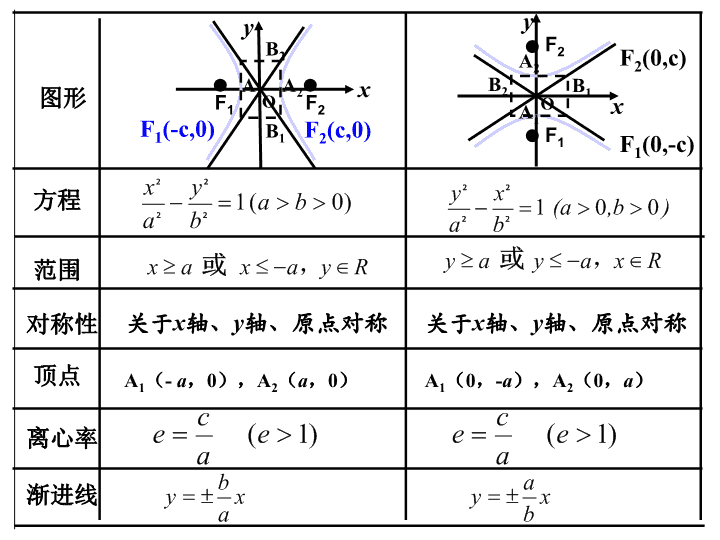
双曲线的性质 ( 二 ) 关于 x 轴、 y 轴、原点对称 图形 方程 范围 对称性 顶点 离心率 y x O A 2 B 2 A 1 B 1 . . F 1 F 2 y B 2 A 1 A 2 B 1 x O . . F 2 F 1 A 1 （ - a ， 0 ）， A 2 （ a ， 0 ） B 1 （ 0 ， -b ）， B 2 （ 0 ， b ） F 1 (-c,0) F 2 (c,0) F 1 (-c,0) F 2 (c,0) 关于 x 轴、 y 轴、原点对称 A 1 （ - a ， 0 ）， A 2 （ a ， 0 ） 渐进线 无 关于 x 轴、 y 轴、原点对称 图形 方程 范围 对称性 顶点 离心率 A 1 （ - a ， 0 ）， A 2 （ a ， 0 ） A 1 （ 0 ， - a ）， A 2 （ 0 ， a ） 关于 x 轴、 y 轴、原点对称 渐进线 . . y B 2 A 1 A 2 B 1 x O F 2 F 1 x B 1 y O . F 2 F 1 B 2 A 1 A 2 . F 1 (-c,0) F 2 (c,0) F 2 (0,c) F 1 (0,-c) 1 、“共渐近线”的双曲线 λ>0 表示焦点在 x 轴上的双曲线； λ<0 表示焦点在 y 轴上的双曲线。 2 、“共焦点”的双曲线 （ 1 ）与椭圆 有共同焦点的双曲线方程表 示为 （ 2 ）与双曲线 有共同焦点的双曲线方 程表示为 复习练习： 2. 求与椭圆 有共同焦点，渐近线方程为 的双曲线方程。 3 、求以椭圆 的焦点为顶点，以椭圆的 顶点为焦点的双曲线的方程。 例 1 、双曲线型自然通风塔的外形，是双曲线 　　的一部分绕其虚轴旋转所成的曲面，它的 　　最小半径为 12m, 上口半径为 13m, 下口半径 　　为 25m, 高 55m. 选择适当的坐标系，求出此 　　双曲线的方程 ( 精确到 1m). A′ A 0 x C′ C B′ B y 13 12 25 例题讲解 例 2 、点 M （ x,y ）与定点 F （ 5,0 ），的距离 和它到定直线　： 的距离的比是常 数 , 求点 M 的轨迹 . 　 y 0 d 直线与双曲线问题： 例 3 、如图，过双曲线 的右焦点 倾斜角为 的直线交双曲线于 A ， B 两点，求 |AB| 。 切点三角形 例 4 、由双曲线 上的一点 P 与左、右 两焦点 构成 ，求 的内切圆与 边 的切点坐标。 说明： 双曲线上一点 P 与双曲线的两个焦点 构成的三角形称之为 焦点三角形 ，其中 和 为三角形的三边。解决与这个三角形有关的问题，要充分利用双曲线的定义和三角形的边角关系、正弦定理、余弦定理。 例 5 、设双曲线 C ： 与直线 相交于两个不同的点 A 、 B 。 （ 1 ）求双曲线 C 的离心率 e 的取值范围。 （ 2 ）设直线 l 与 y 轴的交点为 P ，且 求 a 的值。 练习： 1 、已知双曲线 ，过点 P(1,1) 的直线 l 与 双曲线只有一个公共点，求直线 l 的斜率。