专题43+空间向量及其运算（押题专练）-2018年高考数学（理）一轮复习精品资料 8页

专题43+空间向量及其运算 ‎1．在空间直角坐标系中，A(1，2，3)，B(－2，－1，6)，C(3，2，1)，D(4，3，0)，则直线AB与CD的位置关系是(　　)‎ A．垂直　　　　　　　B．平行 C．异面 D．相交但不垂直 解析：由题意得，＝(－3，－3，3)，＝(1，1，－1)，‎ ‎∴＝－3，∴与共线，‎ 又与没有公共点．∴AB∥CD.‎ 答案：B ‎2．空间四边形ABCD的各边和对角线均相等，E是BC的中点，那么(　　)‎ A.·<· B.·＝· C.·>· D.·与·的大小不能比较 解析：取BD的中点F，连接EF，则EFCD.‎ 因为AE⊥BC，〈，〉＝〈，〉>90°.‎ 所以·＝0，·<0，‎ 因此·>·.‎ 答案：C ‎3． O为空间任意一点，若＝＋＋，则A，B，C，P四点(　　)‎ A．一定不共面 B．一定共面 C．不一定共面 D．无法判断 解析：∵＝＋＋，‎ 且＋＋＝1.所以P，A，B，C四点共面．‎ 答案：B ‎4．已知向量a＝(1，1，0)，b＝(－1，0，2)，且ka＋b与2a－b互相垂直，则k的值是(　　)‎ A．－1　　　B.　　　C.　　　D. 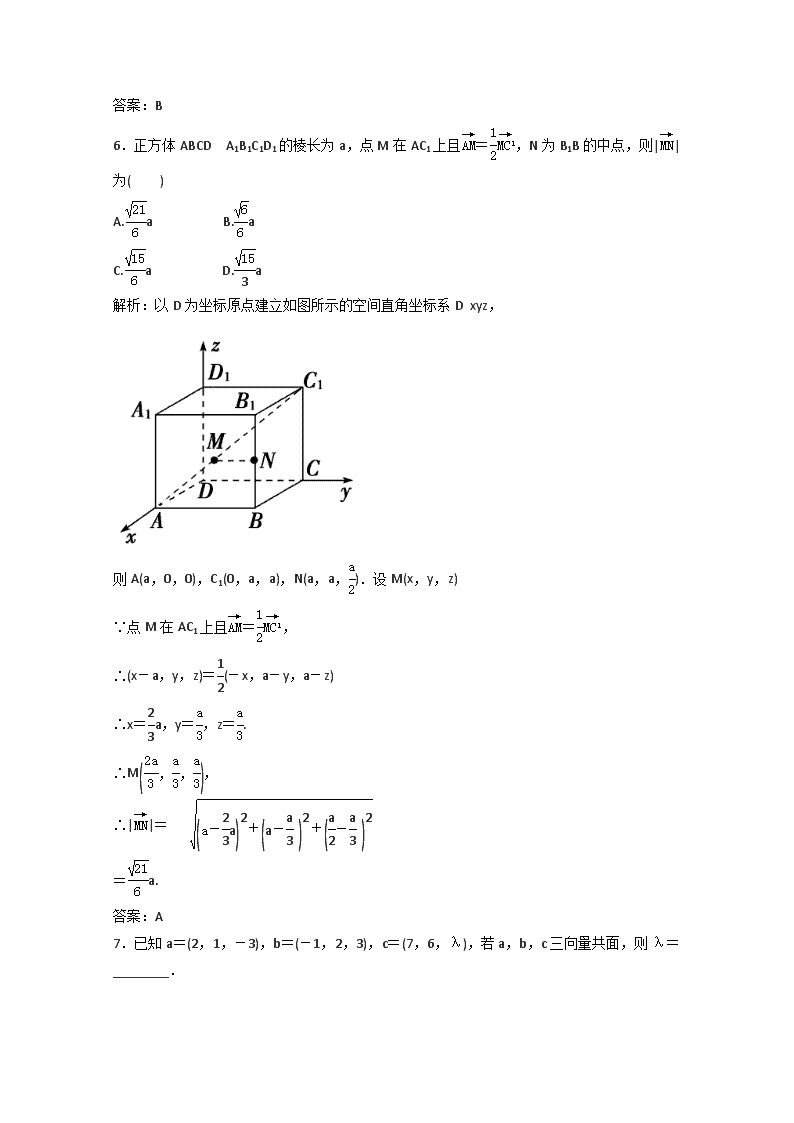‎5． 在空间四边形ABCD中，则·＋·＋·的值为 (　　)‎ A．－1 B．0 C．1 D．2‎ 解析：如图，令＝a，＝b，＝c.‎ 则·＋·＋· ‎＝a·(c－b)＋b·(a－c)＋c·(b－a)＝a·c－a·b＋b·a－b·c＋c·b－c·a＝0.‎ 答案：B ‎6．正方体ABCDA1B1C1D1的棱长为a，点M在AC1上且＝，N为B1B的中点，则||为(　　)‎ A.a B.a C.a D.a 解析：以D为坐标原点建立如图所示的空间直角坐标系Dxyz，‎ 则A(a，0，0)，C1(0，a，a)，N(a，a，)．设M(x，y，z)‎ ‎∵点M在AC1上且＝，‎ ‎∴(x－a，y，z)＝(－x，a－y，a－z)‎ ‎∴x＝a，y＝，z＝.‎ ‎∴M，‎ ‎∴||＝ ‎＝a.‎ 答案：A ‎7．已知a＝(2，1，－3)，b＝(－1，2，3)，c＝(7，6，λ)，若a，b，c三向量共面，则λ＝________．‎ ‎8．已知2a＋b＝(0，－5，10)，c＝(1，－2，－2)，a·c＝4，|b|＝12，则以b，c为方向向量的两直线的夹角为________．‎ 解析：由题意得，(2a＋b)·c＝0＋10－20＝－10.‎ 即2a·c＋b·c＝－10，又∵a·c＝4，∴b·c＝－18，‎ ‎∴cos〈b，c〉＝＝＝－，‎ ‎∴〈b，c〉＝120°，∴两直线的夹角为60°.‎ 答案：60°‎ ‎9．已知O(0，0，0)，A(1，2，3)，B(2，1，2)，P(1，1，2)，点Q在直线OP上运动，当·取最小值时，点Q的坐标是________．‎ ‎10．已知空间中三点A(－2，0，2)，B(－1，1，2)，C(－3，0，4)，设a＝，b＝.‎ ‎(1)若|c|＝3，且c∥，求向量c；‎ ‎(2)求向量a与向量b的夹角的余弦值．‎ 解：(1)∵c∥，＝(－3，0，4)－(－1，1，2)＝(－2，－1，2)，‎ ‎∴c＝m＝m(－2，－1，2)＝(－2m，－m，2m)，‎ ‎∴|c|＝＝3|m|＝3，‎ ‎∴m＝±1.‎ ‎∴c＝(－2，－1，2)或(2，1，－2)．‎ ‎(2)∵a＝(1，1，0)，b＝(－1，0，2)，‎ ‎∴a·b＝(1，1，0)·(－1，0，2)＝－1，‎ 又∵|a|＝＝，‎ ‎|b|＝＝，‎ ‎∴cos〈a，b〉＝＝＝－，‎ 即向量a与向量b的夹角的余弦值为－.‎ ‎11．如图，在棱长为a的正方体ABCDA1B1C1D1中，G为△BC1D的重心．‎ ‎(1)试证：A1，G，C三点共线；‎ ‎(2)试证：A1C⊥平面BC1D.‎ 证明：(1)＝＋＋＝＋＋，‎ 可以证明：＝(＋＋)＝，‎ ‎∴∥，即A1，G，C三点共线．‎ ‎(2)设＝a，＝b，＝c，则|a|＝|b|＝|c|＝a，‎ 且a·b＝b·c＝c·a＝0，‎ ‎∵＝a＋b＋c，＝c－a，‎ ‎∴·＝(a＋b＋c)·(c－a)＝c2－a2＝0，‎ 因此⊥，即CA1⊥BC1，同理CA1⊥BD，又BD与BC1是平面BC1D内的两相交直线，故A1C⊥平面BC1D.‎ ‎12．如图所示，在平行六面体ABCD－A1B1C1D1中，设＝a，＝b，＝c，M、N、P分别是AA1、BC、C1D1的中点，试用a，b，c表示以下各向量：‎ ‎ ‎ ‎(1)； (2)；(3)＋。‎ 解析：(1)∵P是C1D1的中点，‎ ‎∴＝＋＋＝a＋＋ ‎＝a＋c＋＝a＋c＋b。‎ ‎(2)∵N是BC的中点，‎ ‎∴＝＋＋＝－a＋b＋ ‎＝－a＋b＋＝－a＋b＋c。‎ ‎(3)∵M是AA1的中点，‎ ‎∴＝＋＝＋ ‎＝－a＋ ‎＝a＋b＋c。‎ 又＝＋＝＋ ‎＝＋＝c＋a，‎ ‎∴＋＝＋ ‎＝a＋b＋c。‎ ‎13．已知a＝(x,4,1)，b＝(－2，y，－1)，c＝(3，－2，z)，a∥b，b⊥c，求：‎ ‎(1)a，b，c；‎ ‎(2)(a＋c)与(b＋c)所成角的余弦值。‎ ‎14．如图所示，在空间直角坐标系中，BC＝2，原点O是BC的中点，点A的坐标是(，，0)，点D在平面yOz内，且∠BDC＝90°，∠DCB＝30°。‎ ‎ ‎ ‎(1)求的坐标；‎ ‎(2)设和的夹角为θ，求cosθ的值。‎ 解析：(1)如图所示，过D作DE⊥BC，垂足为E。在Rt△BDC中，由∠BDC＝90°，∠DCB＝30°，BC＝2，得BD＝1，CD＝。‎ ‎∴DE＝CDsin30°＝。‎ OE＝OB－BDcos60°＝1－＝。‎ ‎∴D点坐标为，‎ 即的坐标为(0，－，)。‎ ‎(2)依题意，＝，＝(0，－1,0)，＝(0,1,0)，‎ ‎∴＝－＝，＝－＝(0,2,0)。‎ 设和的夹角为θ，‎ 则cosθ＝ ‎＝ ‎＝＝－。‎ ‎∴cosθ＝－。‎ ‎ ‎