数学（文）卷·2018届黑龙江省牡丹江市一中高二上学期期末考试（2017-01） 9页

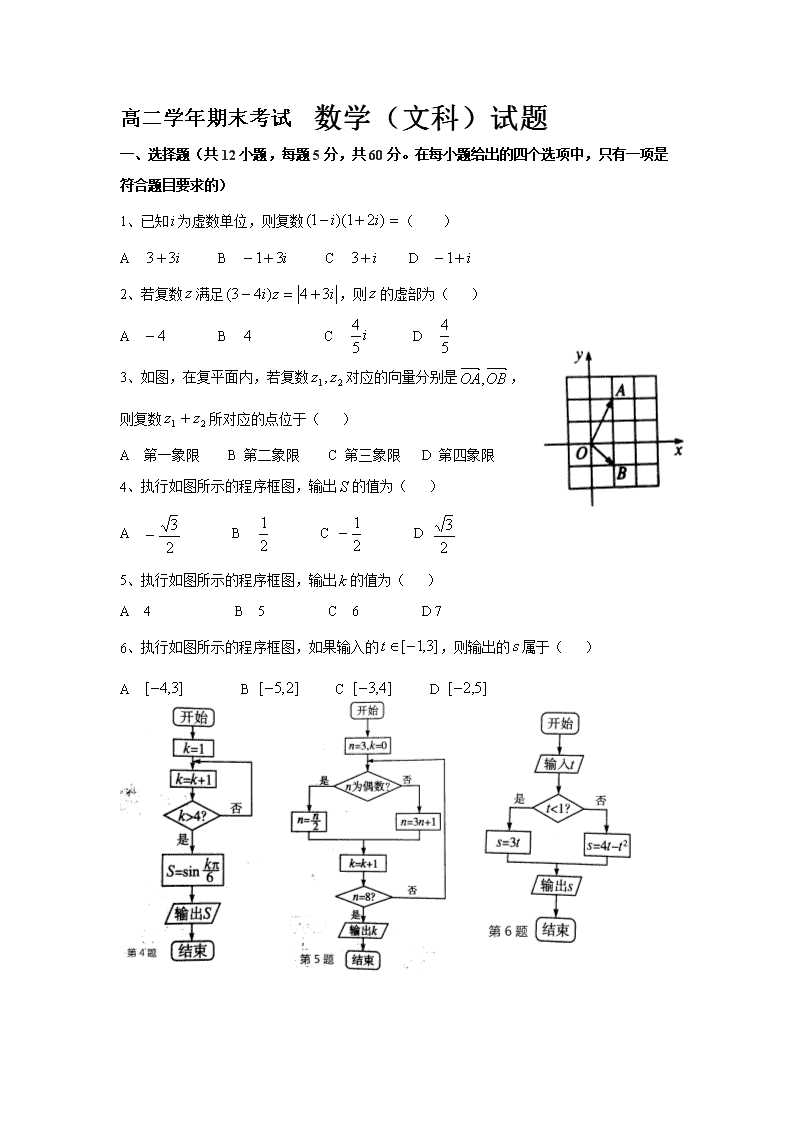
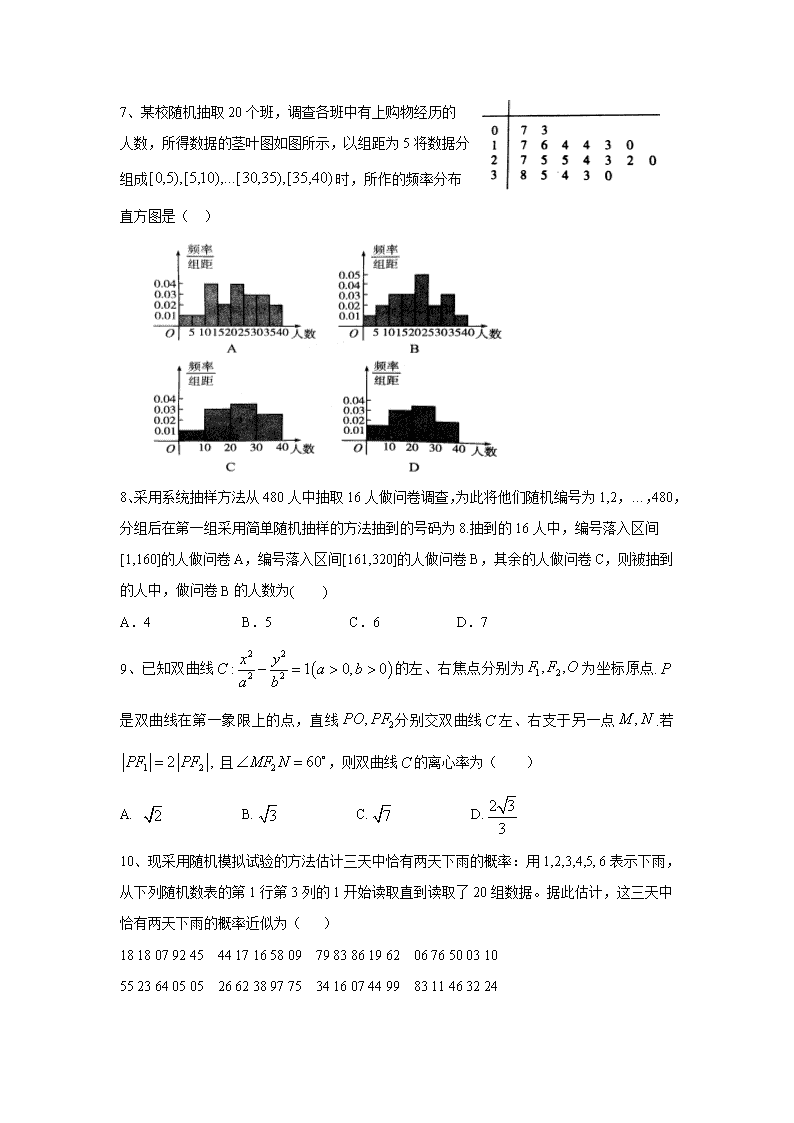
高二学年期末考试 数学（文科）试题 一、选择题（共12小题，每题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1、已知为虚数单位，则复数（ ）‎ A B C D ‎ ‎2、若复数满足，则的虚部为（ ）‎ A B C D ‎ ‎3、如图，在复平面内，若复数对应的向量分别是，‎ 则复数所对应的点位于（ ）‎ A 第一象限 B 第二象限 C 第三象限 D 第四象限 ‎4、执行如图所示的程序框图，输出的值为（ ）‎ A B C D ‎ ‎5、执行如图所示的程序框图，输出的值为（ ）‎ A 4 B 5 C 6 D 7‎ ‎6、执行如图所示的程序框图，如果输入的，则输出的属于（ ） ‎ A B C D ‎ ‎7、某校随机抽取20个班，调查各班中有上购物经历的 人数，所得数据的茎叶图如图所示，以组距为5将数据分 组成时，所作的频率分布 直方图是（ ）‎ ‎8、采用系统抽样方法从480人中抽取16人做问卷调查，为此将他们随机编号为1,2，…，480，分组后在第一组采用简单随机抽样的方法抽到的号码为8.抽到的16人中，编号落入区间[1,160]的人做问卷A，编号落入区间[161,320]的人做问卷B，其余的人做问卷C，则被抽到的人中，做问卷B的人数为(　　)‎ A．4 B．5 C．6 D．7‎ ‎9、已知双曲线的左、右焦点分别为为坐标原点. 是双曲线在第一象限上的点，直线分别交双曲线左、右支于另一点.若, 且，则双曲线的离心率为（ ）‎ A. B. C. D. ‎ ‎10、现采用随机模拟试验的方法估计三天中恰有两天下雨的概率：用1,2,3,4,5, 6表示下雨，从下列随机数表的第1行第3列的1开始读取直到读取了20组数据。据此估计，这三天中恰有两天下雨的概率近似为（ ）‎ ‎18 18 07 92 45 44 17 16 58 09 79 83 86 19 62 06 76 50 03 10‎ ‎55 23 64 05 05 26 62 38 97 75 34 16 07 44 99 83 11 46 32 24‎ A B C D ‎ ‎11、已知△ABC中，∠ABC=600，AB=2，BC=6，在BC上任取一点D，则使△ABD为钝角三角形的概率为（ ）‎ A B C D ‎ ‎12、抛掷一枚质地均匀的骰子，记第次正面向上的点数为，若抛掷次，满足，则称为“幸运数字”，则“幸运数字”为3的概率是（ ）‎ A B C D ‎ 二、填空题 （共4道小题，每题5分，共20分）‎ ‎13、某研究机构对学生的记忆力和判断力进行统计分析，得下表数据：‎ ‎6‎ ‎8‎ ‎10‎ ‎12‎ ‎2‎ ‎3‎ ‎5‎ ‎6‎ 根据上表提供的数据，用最小二乘法求出关于的线性回归方程中的的值为，则为 ‎ ‎14、现从甲、乙、丙3人中随机选派2人参加某项活动，则甲被选中的概率为 ‎ ‎15、2016年底，某高校对100名教师进行绩效考核，依考核分数分为Ⅰ、Ⅱ、Ⅲ、Ⅳ四种等级，其中分数在内为Ⅳ级，有15名；分数在内为Ⅲ级，有40名；分数在内为Ⅱ级，有20名；分数在内为Ⅰ级，有25名。考核评估后，得其频率分布直方图如图所示，估计这100名教师评估得分的中位数是 ‎ ‎16、已知是所在平面内一点， ，现将一点随机落在内，则该点落在内的概率是 ‎ 三、解答题（共6道题，第22题10分，其余各题每题12分，共70分）‎ ‎17、甲、乙两人参加某体育项目训练，近期的五次测试成绩得分统计情况如图 ‎（1）分别求出两人得分的平均数与方差；‎ ‎（2）根据统计图和（1）中得出的结果，请对两人的训练成绩作出评价。‎ ‎18、随着我国经济的发展，居民的储蓄存款逐年增长，设某地区城乡居民人民币储蓄存款（年底余额）如下表：‎ 年份 ‎2012‎ ‎2013‎ ‎2014‎ ‎2015‎ ‎2016‎ 时间代号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 储蓄存款(千亿元)‎ ‎5[‎ ‎6‎ ‎7‎ ‎8‎ ‎10‎ （1） 求关于的回归方程；‎ （2） 用所求回归方程预测该地区2017年（）的人民币储蓄存款。‎ ‎19、一条直线型街道上的两盏路灯之间的距离为120米，由于光线较暗，想在中间再随意安装两盏路灯，顺序为。问与、与、与 之间的距离都不小于30米的概率是多少？‎ ‎20、某工厂有25周岁及以上工人300名，25周岁以下工人200名。为研究工人的日平均生产量是否与年龄有关，现采用分层抽样的方法，从中抽取了100名工人，先统计了他们某月的日平均生产件数，然后按工人年龄在“25周岁及以上”和“25周岁以下”分为两组，再将两组工人的日平均生产件数分为5组：分别加以统计，得到如图所示的频率分布直方图。‎ ‎（1）从样本中日平均生产件数不足60件的工人中随机抽取2人，求至少抽到一名“25周岁以下组”工人的概率；‎ ‎（2）规定日平均生产件数不少于80件者为“生产能手”。请根据已知条件完成列联表，并判断能否在犯错误的概率不超过的前提下认为”生产能手与工人所在的年龄组有关”。‎ ‎21、如图，在平面直角坐标系中，椭圆（）的左、右焦点分别为，（在轴上方）为椭圆上一点，交椭圆于另一点，设 ‎（1）若点的坐标为，且的周长为16，求椭圆的方程；‎ ‎（2）若垂直于轴，且椭圆的离心率，求实数的取值范围。‎ ‎22、在平面直角坐标系中，以坐标原点为极点，轴正半轴为极轴建立坐标系，曲线的参数方程为， 曲线的极坐标方程为， ‎ ‎（1）求曲线的普通方程，曲线的直角坐标方程；‎ ‎（2）曲线与相交于两点，点，求的值。‎ 答案 ‎1--12‎ CDABA CABBD CA ‎13、 14、 15、78.75 16、‎ ‎17、（1） ， ‎ ‎ （2）由可知乙的成绩较稳定，从折线图看，甲的成绩基本呈上升状态，而乙的成绩上下波动，可知甲的成绩在不断提高，而乙的成绩则无明显提高。‎ ‎18、（1）‎ ‎（2）10.8千亿元 ‎19、‎ ‎20、（1）‎ ‎ (2)‎ 生产能手 非生产能手 合计 ‎25周岁及以上组 ‎15‎ ‎45‎ ‎60‎ ‎25周岁以下组 ‎15‎ ‎25‎ ‎40‎ 合计 ‎30‎ ‎70‎ ‎100‎ 因为，所以在犯错误不超过0.10的前提下不能推断“生产能手与工人所在的年龄组有关”。‎ ‎21、‎ ‎22、（1） ‎ ‎（2）‎