山东省学业水平考试数学模拟试题04 5页

山东省学业水平考试数学模拟试题04‎ 一、选择题（本大题有15小题，每小题3分，共45分。在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1满足条件M{0，1，2}的集合共有（　 ）A．3个　　B．6个　　　 C．7个　　D．8个 ‎2已知，，则=（ ）A、 B、 C、 D、‎ ‎3某公司在甲、乙、丙三个城市分别有180个、150个、120个销售点，公司为了调查产品销售的情况，需从这450个销售点中抽取一个容量为90的样本，记这项调查为①; 某学校高二年级有25名足球运动员，要从中选出5名调查学习负担情况，记这项调查为②；则完成①②这两项调查宜采用的抽样方法依次是（ 　） A．系统抽样，分层抽样B．简单随机抽样，分层抽样C．分层抽样，简单随机抽样 D．分层抽样，系统抽样 ‎4已知集合，，则集合等于（　　）‎ A． B． C． D．‎ ‎5在复平面中，已知点A（2，1），B（0，2），C（-2，1），O（0，0）．给出下面的结论：‎ ‎①直线OC与直线BA平行②③④．‎ 其中正确结论的个数是（ ）A．1个　　B．2个　 C．3个　　D．4个 ‎6下列不等式中, 错误的是（ ）A.B. C. D. ‎ ‎7 在等比数列中，若，则（ ）A．-2 B．2 C．-4 D．4‎ ‎8 的最小正周期为（ ）A B C D ‎ ‎9的值是（ ）A B C D 0‎ ‎10 函数的部分图象如右图，则、可以取的一组值是（ ）‎ x O y ‎1‎ ‎2‎ ‎3‎ ‎ A. B. ‎ ‎ C. D. ‎ ‎11 函数的图象是（ ） ‎ ‎12 在中，角,,的对边分别为,,，若,则角的值为（ ）A. B. C.或 D.或 ‎13已知，且，那么等于（ ）‎ A．－26 B．－18 C．－10 D．10‎ ‎14一条直线若同时平行于两个相交平面，那么这条直线与这两个平面的交线的位置关系是（ ）‎ A．异面 B．相交 C．平行 D．不能确定 ‎15 某农贸市场出售西红柿，当价格上涨时，供给量相应增加，而需求量相应减少，具体调查结果如下表：‎ ‎　 　 表1　市场供给量 表2　市场需求量 单价 ‎（元/kg）‎ ‎2‎ ‎2.4‎ ‎2.8‎ ‎3.2‎ ‎3.6‎ ‎4‎ 单价 ‎（元/kg）‎ ‎4‎ ‎3.4‎ ‎2.9‎ ‎2.6‎ ‎2.3‎ ‎2‎ 供给量 ‎（‎1000kg）‎ ‎50‎ ‎60‎ ‎70‎ ‎75‎ ‎80‎ ‎90‎ 需求量 ‎（‎1000kg）‎ ‎50‎ ‎60‎ ‎65‎ ‎70‎ ‎75‎ ‎80‎ 根据以上提供的信息，市场供需平衡点（即供给量和需求量相等时的单价）应在区间（ 　）‎ ‎ A.（2.3，2.6）内　　B．（2.4，2.6）内　　C．（2.6，2.8）内　　D．（2.8，2.9）内 二、填空题（本大题有5小题，每小题3分，共15分。把答案填在题中的横线上）‎ ‎16．长方体的三条侧棱长的比1：2：3，全面积是88，则长方体的体积是 ‎ ‎17直线得的劣弧所对的圆心角为 ‎ ‎18设、满足约束条件，则的最大值是 ‎ ‎19已知直线与相互平行，则它们之间的距离是 ‎ ‎20．已知的最大值是 ‎ 一、选择题答题卡：班级：_______姓名：___________考号：_______‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ ‎13‎ ‎14‎ ‎15‎ 答案 二、填空题答题卡： 16、_________17、_________18、__________ 19、__________20、__________‎ 三、解答题（本大题有5小题，共40分。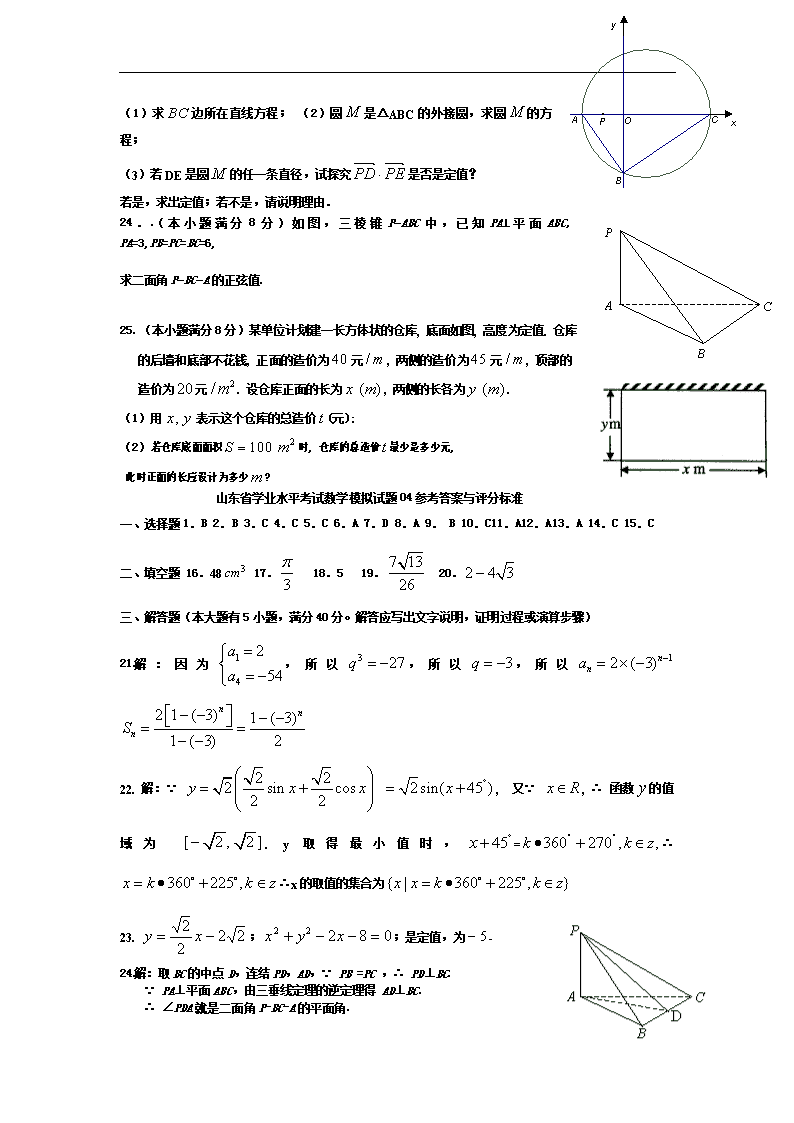解答应写出文字说明，证明过程或演算步骤）‎ ‎21．（本小题满分8分） 在等比数列中 ，求及前项和．‎ ‎22．（本小题满分8分）求函数的值域及y取得最小值时x的取值的集合.‎ ‎23．（本小题满分8分）如图，直角三角形的顶点坐标，直角顶点，顶点在轴上，点为线段的中点 ‎（1）求边所在直线方程； （2）圆是△ABC的外接圆，求圆的方程；‎ ‎（3）若DE是圆的任一条直径，试探究是否是定值？‎ 若是，求出定值；若不是，请说明理由．‎ ‎24．（本小题满分8分）如图，三棱锥P-ABC中，已知PA^平面ABC, PA=3,PB=PC=BC=6, ‎ 求二面角P-BC-A的正弦值 ‎ ‎25 （本小题满分8分）某单位计划建一长方体状的仓库, 底面如图, 高度为定值. 仓库的后墙和底部不花钱, 正面的造价为元, 两侧的造价为元, 顶部的造价为元. 设仓库正面的长为, 两侧的长各为. ‎ ‎（1）用表示这个仓库的总造价(元);‎ ‎（2）若仓库底面面积时, 仓库的总造价最少是多少元,‎ ‎ 此时正面的长应设计为多少?‎ ‎ 山东省学业水平考试数学模拟试题04参考答案与评分标准 一、选择题1．B 2．B 3．C 4．C 5．C 6．A 7．D 8．A 9． B 10．C11．A12．A13．A 14．C 15．C 二、填空题 16．48 17． 18．5 19． 20．‎ 三、解答题（本大题有5小题，满分40分。解答应写出文字说明，证明过程或演算步骤）‎ ‎21解：因为，所以，所以，所以 ‎ ‎22. 解：∵ , 又∵ , ∴ 函数的值域为 . y取得最小值时，=∴∴x的取值的集合为 ‎23. ；；是定值，为-‎ ‎24解：取BC的中点D，连结PD，AD，∵ PB =PC ，∴ PD⊥BC ‎　　∵ PA⊥平面ABC，由三垂线定理的逆定理得 AD⊥BC ‎ ‎　　∴ ∠PDA就是二面角P-BC-A的平面角 ‎ ‎　　∵ PB = PC = BC = 6 ，∴ PD = ‎ ‎　　sin∠PDA= 即二面角P-BC-A的正弦值是 ‎ ‎25. 解: 解：⑴ 由题意得仓库的总造价为：…… 3分 ‎⑵ 仓库底面面积时, ‎ ‎… 5分当且仅当时, 等号成立, … 6分又∵ , ∴ .… 7分 答：仓库底面面积时, 仓库的总造价最少是元, 此时正面的长应设计为. 8分 向量补练题 ‎1.下列向量组中，能作为平面内所有向量基底的是 ( )‎ A B. ‎ C.  D. ‎ ‎2.如图，若，，，则向量可用，表示为（ ）‎ A.B. C. D.‎ ‎3.下列各式计算正确的是（ ）‎ ‎(1)(－7)‎6a=-42a (2)7(a+b)－8b=‎7a+15b (3)a－2b+a+2b=2a (4)若a=m+n,b=‎4m+4n,则a∥b A．1个 B．2个 C．3个 D．4个 ‎4.若化简=（ ）A．B．C．D． 以上都不对 ‎5.已知、是实数，、是向量，对于一下命题正确的是__________．‎ ‎① ②‎ ‎③若，则 ④若，则 ‎6.=__________．‎ ‎7.已知向量，，且，则=__________．‎ ‎8.若向量，当＝_____时与共线且方向相同.‎ ‎9.则向量在向量方向上的投影为_________‎ ‎10. ABCD的3个顶点为A(a,b),B(-b,a),C(0,0)，则它的第4个顶点D的坐标是_________‎ ‎11. 已知向量=（2，2），，则向量的模的最大值是 ‎