2019届二轮复习算法初步学案（全国通用） 8页

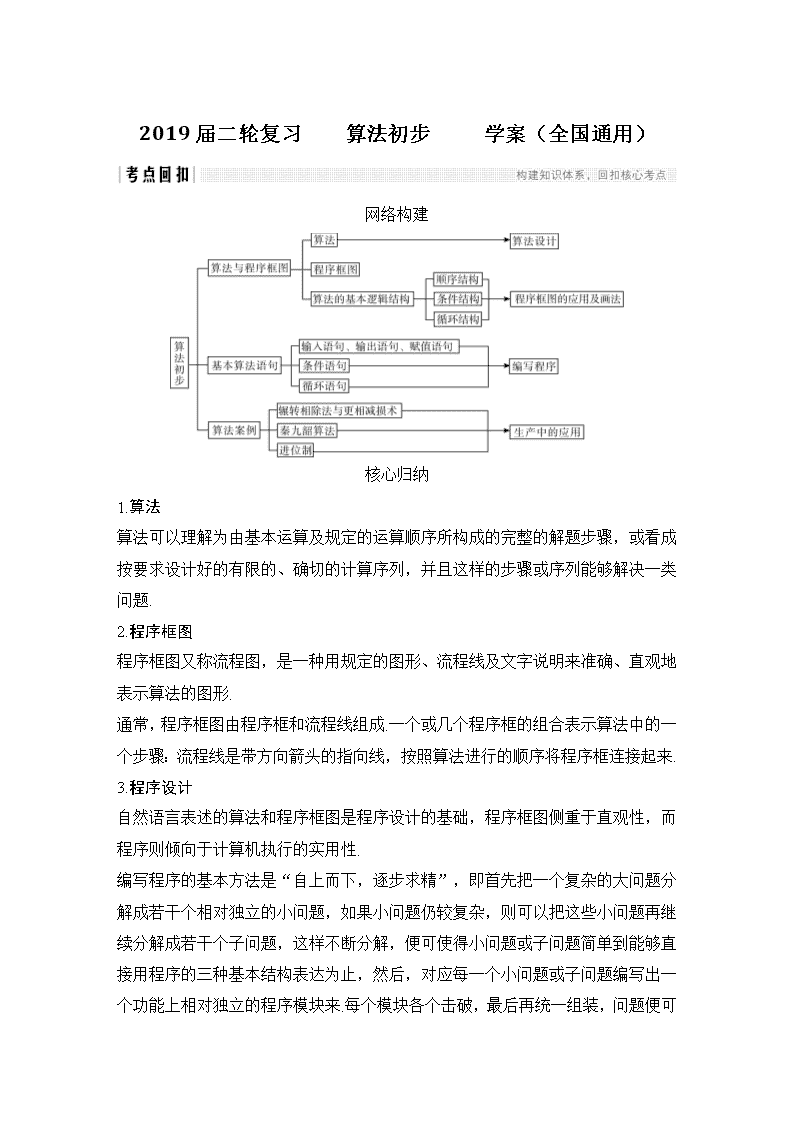
‎2019届二轮复习 算法初步 学案（全国通用）‎ 网络构建 核心归纳 ‎1.算法 算法可以理解为由基本运算及规定的运算顺序所构成的完整的解题步骤，或看成按要求设计好的有限的、确切的计算序列，并且这样的步骤或序列能够解决一类问题.‎ ‎2.程序框图 程序框图又称流程图，是一种用规定的图形、流程线及文字说明来准确、直观地表示算法的图形.‎ 通常，程序框图由程序框和流程线组成.一个或几个程序框的组合表示算法中的一个步骤：流程线是带方向箭头的指向线，按照算法进行的顺序将程序框连接起来.‎ ‎3.程序设计 自然语言表述的算法和程序框图是程序设计的基础，程序框图侧重于直观性，而程序则倾向于计算机执行的实用性.‎ 编写程序的基本方法是“自上而下，逐步求精”，即首先把一个复杂的大问题分解成若干个相对独立的小问题，如果小问题仍较复杂，则可以把这些小问题再继续分解成若干个子问题，这样不断分解，便可使得小问题或子问题简单到能够直接用程序的三种基本结构表达为止，然后，对应每一个小问题或子问题编写出一个功能上相对独立的程序模块来.每个模块各个击破，最后再统一组装，‎ 问题便可得到解决.‎ ‎4.算法在实际生活中的应用 算法的基本思想在我们的日常生活中是很有用的，随着计算机技术的发展，计算机技术在实际生活中的应用越来越广泛，特别是尖端科学技术更离不开它，算法在计算机科学和数学领域都有非常重要的地位.为此，我们在理解算法的基础上，要有意识地将算法思想应用到日常生活中，这样有利于提高解决具体问题的能力.‎ 要点一　算法的设计 算法设计的一般步骤 ‎(1)认真分析所给的问题，找出解决该类问题的一般方法.‎ ‎(2)借助于一般变量或参数对算法进行描述.‎ ‎(3)将解决问题的过程分解为若干个步骤.‎ ‎(4)用简洁的语言将各个步骤表述出来.‎ ‎【例1】　求两底面直径分别为2和4，且高为4的圆台的表面积及体积，写出解决该问题的算法.‎ 解　算法如下：第一步，取r1＝1，r2＝2，h＝4.‎ 第二步，计算l＝.‎ 第三步，计算S＝πr＋πr＋π(r1＋r2)l与V＝π(r＋r＋r1r2)h.‎ 第四步，输出计算结果.‎ ‎【训练1】　已知平面直角坐标系中的两点A(－1，0)，B(3，2)，写出求线段AB的垂直平分线的一个算法.‎ 解　算法如下：‎ 第一步，计算x0＝＝1，y0＝＝1，得线段AB的中点N(1，1).‎ 第二步，计算kAB＝＝.‎ 第三步，计算k＝－＝－2，即线段AB垂直平分线的斜率.‎ 第四步，由直线的点斜式方程得线段AB的垂直平分线的方程：y－1＝－2(x－1)，即2x＋y－3＝0.‎ 要点二　程序框图的画法及识图 画程序框图的规则 ‎(1)使用标准的图形符号.‎ ‎(2)框图一般按从上到下、从左到右的方向画.‎ ‎(3)除判断框外，大多数流程图符号只有一个进入点和一个退出点.判断框是具有超过一个退出点的唯一符号.‎ ‎(4)判断框分两大类，一类判断框是“是”与“否”两分支的判断，而且有且仅有两个结果；另一类是多分支判断，有几种不同的结果.‎ ‎(5)在图形符号内描述的语言要简练、清楚.‎ ‎【例2】　(1)阅读如图所示的程序框图，运行相应的程序，输出的结果是(　　)‎ A.32 B.16‎ C.8 D.4‎ ‎(2)求满足1＋2＋3＋4＋…＋n>500的最小的正整数n，画出执行该问题的程序框图.‎ ‎(1)解析　根据程序框图依次执行：S＝＝－，n＝2；S＝＝，n＝4；S＝＝3，n＝8，S＝3>1，故跳出循环，所以输出结果为8.‎ 答案　C ‎(2)解　程序框图：‎ ‎【训练2】　执行如图所示的程序框图，若输入x的值为2，则输出x的值为(　　)‎ A.25 B.24‎ C.23 D.22‎ 解析　x＝2，n＝1，进入循环；‎ x＝2×2＋1＝5，n＝2；‎ x＝2×5＋1＝11，n＝3；‎ x＝2×11＋1＝23，n＝4，此时，n>3，故跳出循环，输出的x的值为23.‎ 答案　C 要点三　算法语句的设计及应用 基本算法语句有输入语句、输出语句、赋值语句、条件语句和循环语句五种，用基本算法语句编写程序时，要注意各种语句的格式要求，特别是条件语句和循环语句，还要注意这两类语句中判断条件的表达及循环语句中有关变量的取值范围.‎ ‎【例3】　用砖砌一堵墙，第一层用了全部砖的一半多一块；第二层用了剩下砖的一半又多一块，以后每层都用了前一层砌完后剩下砖的一半多一块，到第二十层时恰好剩下一块砖，将其砌上，这堵墙也就砌完了.‎ 画出计算这堵墙用砖块数的程序框图并编写程序.‎ 解　第二十层砌前有砖：S20＝1(块)；‎ 第十九层砌前有砖：S19＝(1＋1)×2＝4(块)；‎ 第十八层砌前有砖：S18＝(1＋4)×2＝10(块)；‎ ‎……‎ 第一层砌前有砖：‎ S1＝(S2＋1)×2(块).‎ 所以递推关系式是：‎ S20＝1，Sn＝(Sn＋1＋1)×2，n＝1，2，…，19.‎ 故可用循环结构设计算法.‎ 程序框图如图所示.‎ ‎　‎ 程序如下：‎ S＝1‎ i＝1‎ WHILE　i＜20‎ S＝2*(S＋1)‎ i＝i＋1‎ WEND PRINT　S END ‎【训练3】　给出30个数：1，2，4，7，…，其规律是：第1个数是1，第2个数比第1个数大1，第3个数比第2个数大2，第4个数比第3个数大3，依此类推，要计算第30个数的大小，现在已给出了该问题算法的程序框图(如图).‎ ‎(1)请在图中判断框①处和执行框②处填上合适的语句，使之能完成该题算法功能；‎ ‎(2)根据程序框图写出程序.‎ 解　(1)①i>30？　②P＝P＋i ‎(2)程序如下：‎ P＝1‎ S＝0‎ i＝1‎ DO ‎　S＝S＋P ‎　P＝P＋i ‎　i＝i＋1‎ LOOP UNTIL i>30‎ PRINT S END 要点四　算法案例 算法案例包含三方面的内容：辗转相除法与更相减损术、秦九韶算法、进位制.利用辗转相除法或更相减损术可以求两个正数的最大公约数，利用秦九韶算法可以求多项式的值，利用进位制的知识，可以进行进位制之间的转化.‎ ‎【例4】　(1)把五进制数1231(5)化为七进制数为________.‎ ‎(2)378与90的最大公约数为________.‎ 解析　(1)1231(5)＝1×53＋2×52＋3×51＋1×50＝191，‎ 故1231(5)＝362(7).‎ ‎(2)∵378与90都是偶数，∴用2约简得189和45，‎ ‎189－45＝144，‎ ‎144－45＝99，‎ ‎99－45＝54，‎ ‎54－45＝9，‎ ‎45－9＝36，‎ ‎36－9＝27，‎ ‎27－9＝18，‎ ‎18－9＝9.‎ ‎∴378与90的最大公约数是2×9＝18.‎ 答案　(1)362(7)　(2)18‎ ‎【训练4】　用秦九韶算法求多项式f(x)＝2＋0.35x＋1.8x2－3.66x3＋6x4－5.2x5＋x6在x＝－1.3的值时，令v0＝a6，v1＝v0x＋a5，…，v6＝v5x＋a0时，v3的值为________.‎ 解析　∵v0＝1，v1＝x－5.2＝－1.3－5.2＝－6.5，‎ v2＝v1x＋6＝(－6.5)×(－1.3)＋6＝14.45，∴v3＝v2x－3.66＝14.45×(－1.3)－3.66＝－22.445.‎ 答案　－22.445‎