数学卷·2018届黑龙江省牡丹江一中高二上学期开学数学试卷 （解析版） 24页

‎2016-2017学年黑龙江省牡丹江一中高二（上）开学数学试卷 ‎　‎ 一、选择题：（每小题5分，共60分）‎ ‎1．算法的三种基本结构是（　　）‎ A．顺序结构、模块结构、条件结构 B．顺序结构、循环结构、模块结构 C．顺序结构、条件结构、循环结构 D．模块结构、条件结构、循环结构 ‎2．一个年级有12个班，每个班有50名同学，随机编号为1～50，为了了解他们在课外的兴趣，要求每班第40号同学留下来进行问卷调查，这里运用的抽样方法是（　　）‎ A．抽签法 B．分层抽样法 C．随机数表法 D．系统抽样法 ‎3．一个三位数字的密码锁，每位上的数字都在0到9这十个数字中任选，某人忘记了密码最后一个号码，那么此人开锁时，在对好前两位数码后，随意拨动最后一个数字恰好能开锁的概率为（　　）‎ A． B． C． D．‎ ‎4．设i为虚数单位，若复数z=（m2+2m﹣8）+（m﹣2）i是纯虚数，则实数m=（　　）‎ A．2 B．﹣4或2 C．2或﹣4 D．﹣4‎ ‎5．假设吉利公司生产的“远景”、“金刚”、“自由舰”三种型号的轿车产量分别是1600辆、6000辆和2000辆，为检验公司的产品质量，现从这三种型号的轿车中抽取48辆进行检验，这三种型号的轿车依次应抽取（　　）‎ A．16，16，16 B．8，30，10 C．4，33，11 D．12，27，9‎ ‎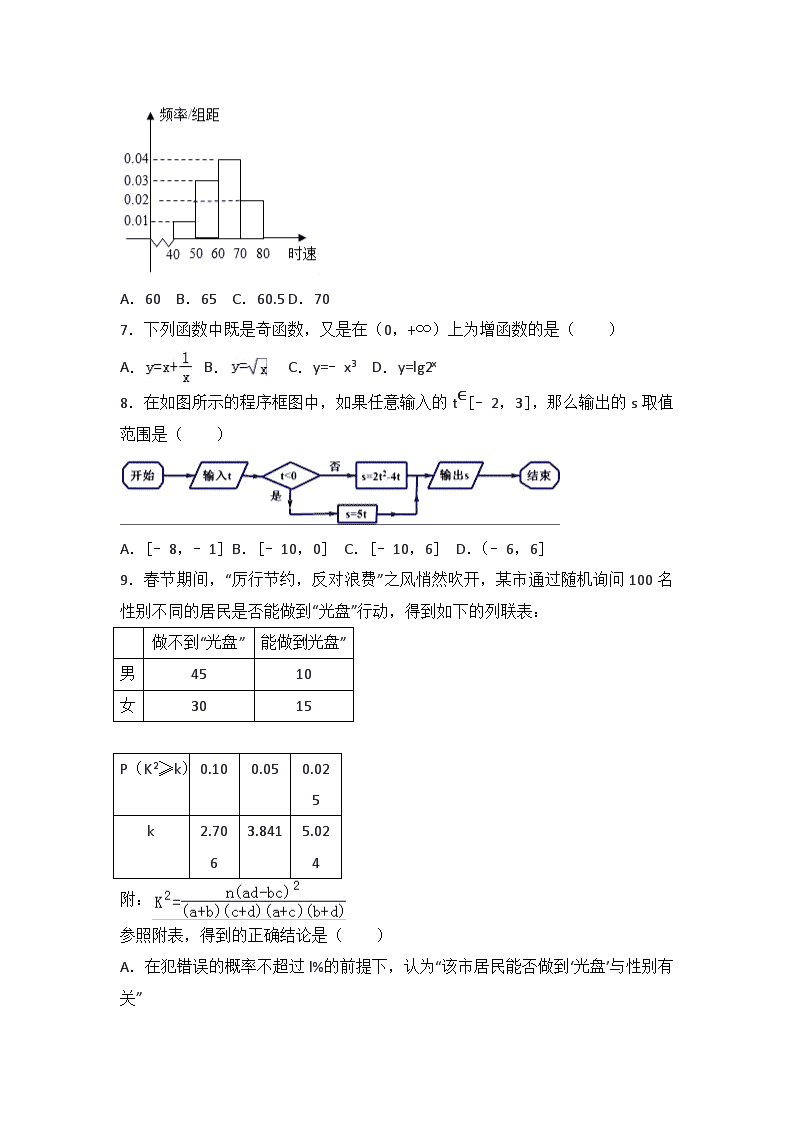6．已知200辆汽车通过某一段公路时的时速的频率分布直方图如图所示，估计这辆汽车在这段公路时速的众数是（　　）‎ A．60 B．65 C．60.5 D．70‎ ‎7．下列函数中既是奇函数，又是在（0，+∞）上为增函数的是（　　）‎ A． B． C．y=﹣x3 D．y=lg2x ‎8．在如图所示的程序框图中，如果任意输入的t∈[﹣2，3]，那么输出的s取值范围是（　　）‎ A．[﹣8，﹣1] B．[﹣10，0] C．[﹣10，6] D．（﹣6，6]‎ ‎9．春节期间，“厉行节约，反对浪费”之风悄然吹开，某市通过随机询问100名性别不同的居民是否能做到“光盘”行动，得到如下的列联表：‎ 做不到“光盘”‎ 能做到“光盘”‎ 男 ‎45‎ ‎10‎ 女 ‎30‎ ‎15‎ P（K2≥k）‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ k ‎2.706‎ ‎3.841‎ ‎5.024‎ 附：‎ 参照附表，得到的正确结论是（　　）‎ A．在犯错误的概率不超过l%的前提下，认为“该市居民能否做到‘光盘’与性别有关”‎ B．在犯错误的概率不超过l%的前提下，认为“该市居民能否做到‘光盘’与性别无关”‎ C．有90%以上的把握认为“该市居民能否做到‘光盘’与性别有关”‎ D．有90%以上的把握认为“该市居民能否做到‘光盘’与性别无关”‎ ‎10．某赛季甲、乙两名篮球运动员各13场比赛得分情况用茎叶图表示如下：根据上图，对这两名运动员的成绩进行比较，下列四个结论中，不正确的是（　　）‎ A．甲运动员得分的极差大于乙运动员得分的极差 B．甲运动员得分的中位数大于乙运动员得分的中位数 C．甲运动员的得分平均值大于乙运动员的得分平均值 D．甲运动员的成绩比乙运动员的成绩稳定 ‎11．过抛物线y2=4x（p＞0）的焦点作两条互相垂直的弦AB、CD，则=（　　）‎ A．2 B．4 C． D．‎ ‎12．已知函数f（x）=log2x﹣2log2（x+c），其中c＞0．若对于任意的x∈（0，+∞），都有f（x）≤1，则c的取值范围是（　　）‎ A． B． C． D．‎ ‎　‎ 二、填空题（每小题5分，共20分）‎ ‎13．已知点 F 是抛物线 y2=4x的焦点，M、N 是该抛物线上两点，‎ ‎|MF|+|NF|=6，则 MN中点的横坐标为　　．‎ ‎14．在棱长为3的正方体内任取一点P，则点P到正方体各个面的距离都不小于1的概率为　　．‎ ‎15．某单位为了了解用电量y度与气温x℃之间的关系，随机统计了某四天的用电量与当天气温，列表如下：‎ 由表中数据得到回归直线方程=﹣2x+a．据此预测当气温为﹣4°C时，用电量为　　（单位：度）．‎ 气温（x℃）‎ ‎18‎ ‎13‎ ‎10‎ ‎﹣1‎ 用电量（度）‎ ‎24‎ ‎34‎ ‎38‎ ‎64‎ ‎16．已知F1，F2是椭圆和双曲线的公共焦点，P是它们的一个公共点，且∠F1PF2=，椭圆的离心率为e1，双曲线的离心率e2，则=　　．‎ ‎　‎ 三、解答题（17题10分，其余每题12分，总计70分）‎ ‎17．对甲、乙的学习成绩进行抽样分析，各抽5门功课，得到的观测值如下：问：甲、乙谁的平均成绩最好？谁的各门功课发展较平衡？‎ 甲 ‎60‎ ‎80‎ ‎70‎ ‎90‎ ‎70‎ 乙 ‎80‎ ‎60‎ ‎70‎ ‎80‎ ‎75‎ ‎18．某校要从艺术节活动中所产生的4名书法比赛一等奖的同学和2名绘画比赛一等奖的同学中选出2名志愿者，参加广州亚运会的服务工作．求：‎ ‎（1）选出的2名志愿者都是获得书法比赛一等奖的同学的概率；‎ ‎（2）选出的2名志愿者中1名是获得书法比赛一等奖，另1名是获得绘画比赛一等奖的同学的概率．‎ ‎19．选修4﹣4：坐标系与参数方程 在直角坐标系xOy中，过点作倾斜角为α的直线l与曲线C：x2+y2=1相交于不同的两点M，N．‎ ‎（Ⅰ）写出直线l的参数方程；‎ ‎（Ⅱ）求的取值范围．‎ ‎20．某校从参加高一年级期末考试的学生中抽出60名学生，将其成绩（均为整数）分成六段[40，50），[50，60）…[90，100]后画出如图部分频率分布直方图．观察图形的信息，回答下列问题：‎ ‎（1）求第四小组的频率，并补全这个频率分布直方图；‎ ‎（2）估计这次考试的及格率（60分及以上为及格）和平均分．‎ ‎21．已知曲线C的极坐标方程是ρ=2cosθ，以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，直线L的参数方程是（t为参数）．‎ ‎（1）求曲线C的直角坐标方程和直线L的普通方程；‎ ‎（2）设点P（m，0），若直线L与曲线C交于A，B两点，且|PA|•|PB|=1，求实数m的值．‎ ‎22．动点P（x，y）到定点F（1，0）与到定直线，x=2的距离之比为．‎ ‎（Ⅰ）求P的轨迹方程；‎ ‎（Ⅱ）过点F（1，0）的直线l（与x轴不重合）与（Ⅰ）中轨迹交于两点M、N．探究是否存在一定点E（t，0），使得x轴上的任意一点（异于点E、F）到直线EM、EN的距离相等？若存在，求出t的值；若不存在，说明理由．‎ ‎　‎ ‎2016-2017学年黑龙江省牡丹江一中高二（上）开学数学试卷 参考答案与试题解析 ‎　‎ 一、选择题：（每小题5分，共60分）‎ ‎1．算法的三种基本结构是（　　）‎ A．顺序结构、模块结构、条件结构 B．顺序结构、循环结构、模块结构 C．顺序结构、条件结构、循环结构 D．模块结构、条件结构、循环结构 ‎【考点】排序问题与算法的多样性．‎ ‎【分析】本题是概念型题，算法的三种基本结构是顺序结构、条件结构、循环结构，由此对比四个选项得出正确选项即可．‎ ‎【解答】解：算法的三种基本结构是顺序结构、条件结构、循环结构，‎ 故答案为：C．‎ ‎　‎ ‎2．一个年级有12个班，每个班有50名同学，随机编号为1～50，为了了解他们在课外的兴趣，要求每班第40号同学留下来进行问卷调查，这里运用的抽样方法是（　　）‎ A．抽签法 B．分层抽样法 C．随机数表法 D．系统抽样法 ‎【考点】系统抽样方法．‎ ‎【分析】当总体容量N较大时，采用系统抽样，将总体分成均衡的若干部分指的是将总体分段，分段的间隔要求相等，预先制定的规则指的是：在第1段内采用简单随机抽样确定一个起始编号，在此编号的基础上加上分段间隔的整倍数即为抽样编号．‎ ‎【解答】解：当总体容量N较大时，采用系统抽样，‎ 将总体分成均衡的若干部分指的是将总体分段，‎ 在第1段内采用简单随机抽样确定一个起始编号，‎ 在此编号的基础上加上分段间隔的整倍数即为抽样编号．‎ 故选D．‎ ‎　‎ ‎3．一个三位数字的密码锁，每位上的数字都在0到9这十个数字中任选，某人忘记了密码最后一个号码，那么此人开锁时，在对好前两位数码后，随意拨动最后一个数字恰好能开锁的概率为（　　）‎ A． B． C． D．‎ ‎【考点】古典概型及其概率计算公式．‎ ‎【分析】由已知中一个三位数字的密码锁，每位上的数字都在0到9这十个数字中任选，某人忘记了密码最后一个号码，我们易求出基本事件总数为10，满足条件的基本事件个数为1，代入古典概型概率计算公式，即可求出答案．‎ ‎【解答】解：由于最后一位上取值在0到9这十个数字中任选，‎ 则基本事件共有10种，‎ 其中随意拨动最后一个数字恰好能开锁的基本事件只有一种 故随意拨动最后一个数字恰好能开锁的概率为 故选C．‎ ‎　‎ ‎4．设i为虚数单位，若复数z=（m2+2m﹣8）+（m﹣2）i是纯虚数，则实数m=（　　）‎ A．2 B．﹣4或2 C．2或﹣4 D．﹣4‎ ‎【考点】复数的基本概念．‎ ‎【分析】由实部等于0且虚部不等于0联立不等式组求得实数m的值．‎ ‎【解答】解：∵z=（m2+2m﹣8）+（m﹣2）i是纯虚数，‎ ‎∴，解得：m=﹣4．‎ 故选：D．‎ ‎　‎ ‎5．假设吉利公司生产的“远景”、“金刚”、“自由舰”三种型号的轿车产量分别是1600辆、6000辆和2000辆，为检验公司的产品质量，现从这三种型号的轿车中抽取48辆进行检验，这三种型号的轿车依次应抽取（　　）‎ A．16，16，16 B．8，30，10 C．4，33，11 D．12，27，9‎ ‎【考点】分层抽样方法．‎ ‎【分析】由题意先求出抽样比例，再由此比例计算出在三种型号的轿车抽取的数目．‎ ‎【解答】解：因总轿车数为9600辆，而抽取48辆进行检验，抽样比例为 =，‎ 而三种型号的轿车有显著区别，根据分层抽样分为三层按比例，‎ ‎∵“远景”型号的轿车产量是1600辆，应抽取辆，‎ 同样，得分别从这三种型号的轿车依次应抽取8辆、30辆、10辆．‎ 故选B．‎ ‎　‎ ‎6．已知200辆汽车通过某一段公路时的时速的频率分布直方图如图所示，估计这辆汽车在这段公路时速的众数是（　　）‎ A．60 B．65 C．60.5 D．70‎ ‎【考点】频率分布直方图．‎ ‎【分析】根据频率分布直方图，结合众数的定义，求出这组数据的众数即可．‎ ‎【解答】解：根据频率分布直方图，得；‎ 众数是频率分布直方图中最高的条形图底边中点的横坐标，‎ ‎∴估计汽车通过这段公路时速的众数应是=65．‎ 故选：B．‎ ‎　‎ ‎7．下列函数中既是奇函数，又是在（0，+∞）上为增函数的是（　　）‎ A． B． C．y=﹣x3 D．y=lg2x ‎【考点】奇偶性与单调性的综合．‎ ‎【分析】利用基本函数的奇偶性、单调性逐项判断可得答案．‎ ‎【解答】解：y=x+是奇函数，在（0，1）上单调递减，在（1，+∞）上单调递增，∴在（0，+∞）上不单调，故排除A；‎ y=的定义域为[0，+∞），不关于原点对称，故y=不具备奇偶性，故排除B；‎ y=﹣x3是奇函数，但在（0，+∞）上单调递减，故排除C；‎ y=lg2x的定义域为R，且lg2﹣x==﹣lg2x，∴函数为奇函数，‎ 又t=2x递增，y=lgt递增，∴y=lg2x在（0，+∞）上递增，‎ 故选D．‎ ‎　‎ ‎8．在如图所示的程序框图中，如果任意输入的t∈[﹣2，3]，那么输出的s取值范围是（　　）‎ A．[﹣8，﹣1] B．[﹣10，0] C．[﹣10，6] D．（﹣6，6]‎ ‎【考点】程序框图．‎ ‎【分析】模拟执行程序框图，可得程序框图的功能是计算并输出s=，分类讨论即可得解．‎ ‎【解答】解：模拟执行程序框图，可得程序框图的功能是计算并输出s=，‎ 故：当t∈[﹣2，0），s=5t∈[﹣10，0），‎ 当t∈[0，3]，s=2t2﹣4t∈[﹣2，6]，‎ 综上可得输出的s取值范围是：[﹣10，6]．‎ 故选：C．‎ ‎　‎ ‎9．春节期间，“厉行节约，反对浪费”之风悄然吹开，某市通过随机询问100名性别不同的居民是否能做到“光盘”行动，得到如下的列联表：‎ 做不到“光盘”‎ 能做到“光盘”‎ 男 ‎45‎ ‎10‎ 女 ‎30‎ ‎15‎ P（K2≥k）‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ k ‎2.706‎ ‎3.841‎ ‎5.024‎ 附：‎ 参照附表，得到的正确结论是（　　）‎ A．在犯错误的概率不超过l%的前提下，认为“该市居民能否做到‘光盘’与性别有关”‎ B．在犯错误的概率不超过l%的前提下，认为“该市居民能否做到‘光盘’与性别无关”‎ C．有90%以上的把握认为“该市居民能否做到‘光盘’与性别有关”‎ D．有90%以上的把握认为“该市居民能否做到‘光盘’与性别无关”‎ ‎【考点】独立性检验．‎ ‎【分析】通过图表读取数据，代入观测值公式计算，然后参照临界值表即可得到正确结论．‎ ‎【解答】解：由2×2列联表得到a=45，b=10，c=30，d=15．‎ 则a+b=55，c+d=45，a+c=75，b+d=25，ad=675，bc=300，n=100．‎ 代入，‎ 得k2的观测值k=．‎ 因为2.706＜3.030＜3.841．‎ 所以有90%以上的把握认为“该市居民能否做到‘光盘’与性别有关”．‎ 故选C．‎ ‎　‎ ‎10．某赛季甲、乙两名篮球运动员各13场比赛得分情况用茎叶图表示如下：根据上图，对这两名运动员的成绩进行比较，下列四个结论中，不正确的是（　　）‎ A．甲运动员得分的极差大于乙运动员得分的极差 B．甲运动员得分的中位数大于乙运动员得分的中位数 C．甲运动员的得分平均值大于乙运动员的得分平均值 D．甲运动员的成绩比乙运动员的成绩稳定 ‎【考点】茎叶图；众数、中位数、平均数．‎ ‎【分析】对各个选项分别加以判断：根据极差的定义结合图中的数据，可得出A正确；根据中位数的定义结合图中的数据，可得出B正确；通过计算平均数的公式结合图中的数据，可得出C正确；通过计算方差的公式，结合图中的数据，可得出D不正确．由此可以得出答案．‎ ‎【解答】解：首先将茎叶图的数据还原：‎ 甲运动员得分：19 18 18 26 21 20 35 33 32 30 47 41 40‎ 乙运动员得分：17 17 19 19 22 25 26 27 29 29 30 32 33‎ 对于A，极差是数据中最大值与最小值的差，‎ 由图中的数据可得甲运动员得分的极差为47﹣16=21，乙运动员得分的极差为33﹣17=16，‎ 得甲运动员得分的极差大于乙运动员得分的极差，因此A正确；‎ 对于B，甲数据从小到大排列：18 18 19 20 21 26 30 32 33 35 40 41 47‎ 处于中间的数是30，所以甲运动员得分的中位数是30，同理求得乙数据的中位数是26，‎ 因此甲运动员得分的中位数大于乙运动员得分的中位数，故B正确；‎ 对于C，不难得出甲运动员的得分平均值约为29.23，乙运动员的得分平均值为25.0，‎ 因此甲运动员的得分平均值大于乙运动员的得分平均值，故C正确；‎ 对于D，分别计算甲、乙两个运动员得分的方差，方差小的成绩更稳定．‎ 可以算出甲的方差为：‎ ‎=88.22，‎ 同理，得出乙的方差为：S乙2=29.54‎ 因为乙的方差小于甲的方差，所以乙运动员的成绩比甲运动员的成绩稳定，故D不正确．‎ 故选D ‎　‎ ‎11．过抛物线y2=4x（p＞0）的焦点作两条互相垂直的弦AB、CD，则=（　　）‎ A．2 B．4 C． D．‎ ‎【考点】直线与圆锥曲线的关系；抛物线的简单性质．‎ ‎【分析】设出两直线的倾斜角，利用焦点弦的弦长公式分别表示出|AB|，|CD|即可求得答案．‎ ‎【解答】解：抛物线y2=4x，可知2p=4，‎ 设直线l1的倾斜角为θ，则l2的倾斜角为﹣θ，‎ 过焦点的弦，|AB|=，|CD|==‎ ‎∴=+==，‎ 故选D．‎ ‎　‎ ‎12．已知函数f（x）=log2x﹣2log2（x+c），其中c＞0．若对于任意的x∈（0，+∞），都有f（x）≤1，则c的取值范围是（　　）‎ A． B． C． D．‎ ‎【考点】抽象函数及其应用；函数恒成立问题．‎ ‎【分析】把函数f（x）的解析式代入f（x）≤1后，利用对数式的运算性质变形，去掉对数符号后把参数c分离出来，然后利用二次函数求最值，则c的取值范围可求．‎ ‎【解答】解：由f（x）≤1，得：log2x﹣2log2（x+c）≤1，‎ 整理得：，所以x+c≥，‎ 即c≥（x＞0）．‎ 令（t＞0）．‎ 则．‎ 令g（t）=，其对称轴为．‎ 所以．‎ 则c．‎ 所以，对于任意的x∈（0，+∞），都有f（x）≤1的c的取值范围是．‎ 故选D．‎ ‎　‎ 二、填空题（每小题5分，共20分）‎ ‎13．已知点 F 是抛物线 y2=4x的焦点，M、N 是该抛物线上两点，|MF|+|NF|=6，则 MN中点的横坐标为　2　．‎ ‎【考点】抛物线的简单性质．‎ ‎【分析】根据抛物线的方程求出准线方程，利用抛物线的定义抛物线上的点到焦点的距离等于到准线的距离，列出方程求出x1+x2=4，即可求出MN中点的横坐标．‎ ‎【解答】解：∵F是抛物线y2=4x的焦点 ‎∴F（1，0），准线方程x=﹣1，‎ 设M（x1，y1），N（x2，y2）‎ ‎∴|MF|+|NF|=x1+1+x2+1=6，‎ 解得x1+x2=4，‎ ‎∴线段MN的中点横坐标为2，‎ 故答案为：2．‎ ‎　‎ ‎14．在棱长为3的正方体内任取一点P，则点P到正方体各个面的距离都不小于1的概率为　　．‎ ‎【考点】几何概型．‎ ‎【分析】根据点P与正方体各表面的距离都大于1，则所在的区域为以棱长为1的正方体内，则概率为两正方体的体积之比．‎ ‎【解答】解：符合条件的点P落在棱长为1的正方体内，‎ 根据几何概型的概率计算公式得P==，‎ 故答案为：．‎ ‎　‎ ‎15．某单位为了了解用电量y度与气温x℃之间的关系，随机统计了某四天的用电量与当天气温，列表如下：‎ 由表中数据得到回归直线方程=﹣2x+a．据此预测当气温为﹣4°C时，用电量为　68　（单位：度）．‎ 气温（x℃）‎ ‎18‎ ‎13‎ ‎10‎ ‎﹣1‎ 用电量（度）‎ ‎24‎ ‎34‎ ‎38‎ ‎64‎ ‎【考点】线性回归方程．‎ ‎【分析】求出样本中心（，），代入求出a，结合线性回归方程进行预测即可．‎ ‎【解答】解： =（18+13+10﹣1）=10，‎ ‎=（24+34+38+64）=40，‎ 则﹣20+a=40，‎ 即a=60，‎ 则回归直线方程=﹣2x+60．‎ 当气温为﹣4°C时，用电量为=﹣2×（﹣4）+60=68，‎ 故答案为：68‎ ‎　‎ ‎16．已知F1，F2是椭圆和双曲线的公共焦点，P是它们的一个公共点，且∠F1PF2=，椭圆的离心率为e1，双曲线的离心率e2，则=　4　．‎ ‎【考点】椭圆的简单性质；双曲线的简单性质．‎ ‎【分析】如图所示，设椭圆与双曲线的标准方程分别为：，（ai，bi＞0，a1＞b1，i=1，2），==c2，c＞0．设|PF1|=m，|PF2|=n．可得m+n=2a1，n﹣m=2a2，由于∠F1PF2=，在△PF1F2中，由余弦定理可得：（2c）2=，化简整理即可得出．‎ ‎【解答】解：如图所示，‎ 设椭圆与双曲线的标准方程分别为：，（ai，bi＞0，a1＞b1，i=1，2），‎ ‎==c2，c＞0．‎ 设|PF1|=m，|PF2|=n．‎ 则m+n=2a1，n﹣m=2a2，‎ 解得m=a1﹣a2，n=a1+a2，‎ 由∠F1PF2=，在△PF1F2中，‎ 由余弦定理可得：（2c）2=，‎ ‎∴4c2=+﹣（a1﹣a2）（a1+a2），‎ 化为+，‎ 化为=4．‎ 故答案为：4．‎ ‎　‎ 三、解答题（17题10分，其余每题12分，总计70分）‎ ‎17．对甲、乙的学习成绩进行抽样分析，各抽5门功课，得到的观测值如下：问：甲、乙谁的平均成绩最好？谁的各门功课发展较平衡？‎ 甲 ‎60‎ ‎80‎ ‎70‎ ‎90‎ ‎70‎ 乙 ‎80‎ ‎60‎ ‎70‎ ‎80‎ ‎75‎ ‎【考点】极差、方差与标准差．‎ ‎【分析】先求出甲和乙的平均数，再求出甲和乙的方差，结果甲的平均数大于乙的平均数，甲的方差大于乙的方差，得到结论．‎ ‎【解答】解：，‎ ‎，‎ ‎∵‎ ‎∴甲的平均成绩较好，乙的各门功课发展较平衡．‎ ‎　‎ ‎18．某校要从艺术节活动中所产生的4名书法比赛一等奖的同学和2名绘画比赛一等奖的同学中选出2名志愿者，参加广州亚运会的服务工作．求：‎ ‎（1）选出的2名志愿者都是获得书法比赛一等奖的同学的概率；‎ ‎（2）选出的2名志愿者中1名是获得书法比赛一等奖，另1名是获得绘画比赛一等奖的同学的概率．‎ ‎【考点】古典概型及其概率计算公式．‎ ‎【分析】（1）把4名获书法比赛一等奖的同学编号为1，2，3，4.2名获绘画比赛一等奖的同学编号为5，6．从6名同学中任选2名的所有可能结果共15个，从6名同学中任选2名，都是书法比赛一等奖的所有可能是（1，2），（1，3），（1，4），（2，3），（2，4），（3，4），共6个．根据古典概型概率公式得到结果．‎ ‎（2）本题是一个等可能事件的概率，列举出试验发生包含的事件，共有15个基本事件，选出的2名志愿者中1名是获得书法比赛一等奖，另1名是获得绘画比赛一等奖的列举出共有8种结果，根据概率公式得到结果．‎ ‎【解答】解：把4名获书法比赛一等奖的同学编号为1，2，3，4.2名获绘画比赛一等奖的同学编号为5，6．‎ 从6名同学中任选2名的所有可能结果如下：（1，2），（1，3），（1，4），（1，5），（1，6），（2，3），（2，4），（2，5），（2，6），（3，4），（3，5），（3，6），（4，5），（4，6），（5，6），共15个．‎ ‎（1）从6名同学中任选2名，都是书法比赛一等奖的所有可能是（1，2），（1，3），（1，4），（2，3），（2，4），（3，4），共6个．‎ 所以选出的2名志愿者都是书法比赛一等奖的概率 ‎（2）从6名同学中任选2名，1名是书法比赛一等奖，另1名是绘画比赛一等奖的所有可能是（1，5），（1，6），（2，5），（2，6），（3，5），（3，6），（4，5），（4，6）共8个．‎ 所以选出的2名志愿者1名是书法比赛一等奖，另1名是绘画比赛一等奖的概率是．‎ ‎　‎ ‎19．选修4﹣4：坐标系与参数方程 在直角坐标系xOy中，过点作倾斜角为α的直线l与曲线C：x2+y2=1相交于不同的两点M，N．‎ ‎（Ⅰ）写出直线l的参数方程；‎ ‎（Ⅱ）求的取值范围．‎ ‎【考点】直线的参数方程；直线与圆相交的性质．‎ ‎【分析】（Ⅰ）利用直线的参数方程的意义即可写出；‎ ‎（Ⅱ）把直线的参数方程代入圆的方程，利用根与系数的关系即可求出．‎ ‎【解答】解：（Ⅰ）∵直线l过点且倾斜角为α，‎ ‎∴直线l的参数方程为（t为参数）；‎ ‎（Ⅱ）把（t为参数）代入x2+y2=1，‎ 得，‎ ‎∵直线l与曲线C：x2+y2=1相交于不同的两点M，N，‎ ‎∴△=＞0，‎ 化为．‎ 又，t1t2=2．‎ ‎∴=﹣===，‎ ‎∵，∴．‎ ‎∴的取值范围是．‎ ‎　‎ ‎20．某校从参加高一年级期末考试的学生中抽出60名学生，将其成绩（均为整数）分成六段[40，50），[50，60）…[90，100]后画出如图部分频率分布直方图．观察图形的信息，回答下列问题：‎ ‎（1）求第四小组的频率，并补全这个频率分布直方图；‎ ‎（2）估计这次考试的及格率（60分及以上为及格）和平均分．‎ ‎【考点】频率分布直方图．‎ ‎【分析】（1）在频率分直方图中，小矩形的面积等于这一组的频率，根据频率的和等于1建立等式解之即可；‎ ‎（2）60及以上的分数所在的第三、四、五、六组，从而求出抽样学生成绩的合格率，再利用组中值估算抽样学生的平均分即可．‎ ‎【解答】解：（Ⅰ）因为各组的频率和等于1，故第四组的频率：f4‎ ‎=1﹣（0.025+0.015*2+0.01+0.005）*10=0.3‎ ‎（Ⅱ）依题意，60及以上的分数所在的第三、四、五、六组，‎ 频率和为（0.015+0.03+0.025+0.005）*10=0.75所以，抽样学生成绩的合格率是75%‎ 利用组中值估算抽样学生的平均分45•f1+55•f2+65•f3+75•f4+85•f5+95•f6‎ ‎=45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71‎ 估计这次考试的平均分是71．‎ ‎　‎ ‎21．已知曲线C的极坐标方程是ρ=2cosθ，以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，直线L的参数方程是（t为参数）．‎ ‎（1）求曲线C的直角坐标方程和直线L的普通方程；‎ ‎（2）设点P（m，0），若直线L与曲线C交于A，B两点，且|PA|•|PB|=1，求实数m的值．‎ ‎【考点】参数方程化成普通方程；简单曲线的极坐标方程．‎ ‎【分析】（1）曲线C的极坐标方程是ρ=2cosθ，化为ρ2=2ρcosθ，利用可得直角坐标方程．直线L的参数方程是 ‎（t为参数），把t=2y代入+m消去参数t即可得出．‎ ‎（2）把（t为参数），代入方程：x2+y2=2x化为： +m2﹣2m=0，由△＞0，得﹣1＜m＜3．利用|PA|•|PB|=t1t2，即可得出．‎ ‎【解答】解：（1）曲线C的极坐标方程是ρ=2cosθ，化为ρ2=2ρcosθ，可得直角坐标方程：x2+y2=2x．‎ 直线L的参数方程是（t为参数），消去参数t可得．‎ ‎（2）把（t为参数），代入方程：x2+y2=2x化为： +m2﹣2m=0，‎ 由△＞0，解得﹣1＜m＜3．‎ ‎∴t1t2=m2﹣2m．‎ ‎∵|PA|•|PB|=1=|t1t2|，‎ ‎∴m2﹣2m=±1，‎ 解得，1．又满足△＞0．‎ ‎∴实数m=1，1．‎ ‎　‎ ‎22．动点P（x，y）到定点F（1，0）与到定直线，x=2的距离之比为．‎ ‎（Ⅰ）求P的轨迹方程；‎ ‎（Ⅱ）过点F（1，0）的直线l（与x轴不重合）与（Ⅰ）中轨迹交于两点M、N．探究是否存在一定点E（t，0），使得x轴上的任意一点（异于点E、F）到直线EM、EN的距离相等？若存在，求出t的值；若不存在，说明理由．‎ ‎【考点】轨迹方程；直线与圆锥曲线的综合问题．‎ ‎【分析】（Ⅰ）直接由题意列等式，化简后求得点P的轨迹方程；‎ ‎（Ⅱ）假设存在点E（t，0）满足题设条件，并设出M，N的坐标，分MN和x轴垂直和不垂直讨论，当MN和x轴不垂直时设出直线l的方程，和（Ⅰ）中求得的轨迹方程联立后化为关于x的一元二次方程，由根与系数关系求得M、N的横坐标的和与积，结合x轴平分∠MEN得到KME+KNE=0，进一步转化为含有M、N的横坐标的关系，代入根与系数关系后求得t的值．‎ ‎【解答】解：（Ⅰ）由题意得，，‎ 化简得，x2+2y2=2，即，即点P的轨迹方程；‎ ‎（Ⅱ）若存在点E（t，0）满足题设条件．并设M（x1，y1）、N（x2，y2），‎ 当MN⊥x轴时，由椭圆的对称性可知，x轴上的任意一点（异于点E、F）到直线EM、EN的距离相等．‎ 当MN与x轴不垂直时，设直线l的方程为y=k（x﹣1）（k≠0）．‎ 联立，得（1+2k2）x2﹣4k2x+2k2﹣2=0．‎ ‎∴，‎ 根据题意，x轴平分∠MEN，则直线ME、NE的倾斜角互补，即KME+KNE=0．‎ 设E（t，0），则有（当x1=t或x2=t时不合题意），‎ 又k≠0，∴，‎ 将y1=k（x1﹣1），y2=k（x2﹣1）代入上式，得，‎ 又k≠0，∴，‎ 即，，‎ ‎∴2x1x2﹣（1+t）（x1+x2）+2t=0，‎ 将代入上式，解得t=2．‎ 综上，存在定点E（2，0），使得x轴上的任意一点（异于点E、F）到直线EM、EN的距离相等．‎ ‎　‎ ‎2017年4月19日