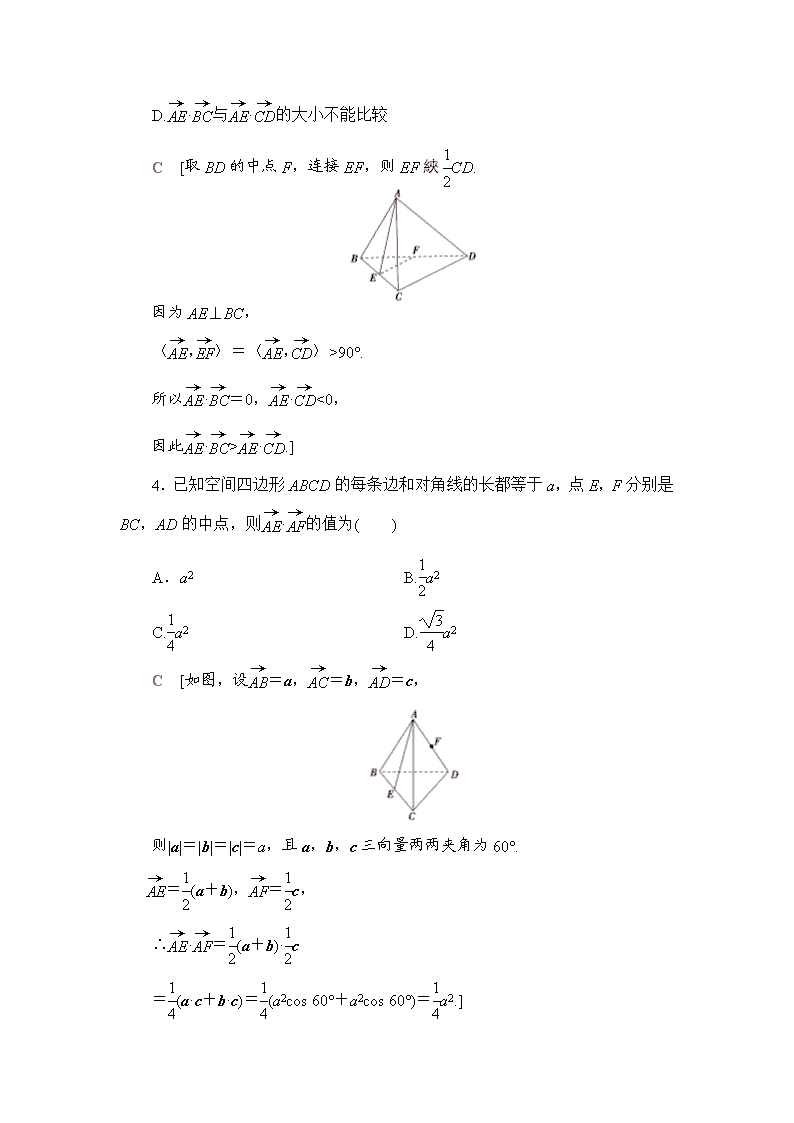2018版高考数学（人教A版理）一轮复习：第7章 第6节 课时分层训练43 7页

课时分层训练(四十三)　空间向量及其运算 A组　基础达标 ‎(建议用时：30分钟)‎ 一、选择题 ‎1．在空间直角坐标系中，A(1,2,3)，B(－2，－1,6)，C(3,2,1)，D(4,3,0)，则直线AB与CD的位置关系是(　　)‎ A．垂直　　　　　　　 B.平行 C．异面 D.相交但不垂直 B　[由题意得，＝(－3，－3,3)，＝(1,1，－1)，‎ ‎∴＝－3，‎ ‎∴与共线，‎ 又与没有公共点．‎ ‎∴AB∥CD.]‎ ‎2．已知a＝(－2,1,3)，b＝(－1,2,1)，若a⊥(a－λb)，则实数λ的值为(　　) ‎ ‎【导学号：01772269】‎ A．－2 B.－ C. D.2‎ D　[由题意知a·(a－λb)＝0，即a2－λa·b＝0，所以14－7λ＝0，解得λ＝2.]‎ ‎3．空间四边形ABCD的各边和对角线均相等，E是BC的中点，那么(　　) ‎ ‎【导学号：01772270】‎ A.·<· B.·＝· C.·>· D.·与·的大小不能比较 C　[取BD的中点F，连接EF，则EF綊CD.‎ 因为AE⊥BC，‎ ‎〈，〉＝〈，〉>90°.‎ 所以·＝0，·<0，‎ 因此·>·.]‎ ‎4．已知空间四边形ABCD的每条边和对角线的长都等于a，点E，F分别是BC，AD的中点，则·的值为(　　)‎ A．a2 B.a2‎ C.a2 D.a2‎ C　[如图，设＝a，＝b，＝c，‎ 则|a|＝|b|＝|c|＝a，且a，b，c三向量两两夹角为60°.‎ ＝(a＋b)，＝c，‎ ‎∴·＝(a＋b)·c ‎＝(a·c＋b·c)＝(a2cos 60°＋a2cos 60°)＝a2.]‎ ‎5．如图767，在大小为45°的二面角AEFD中，四边形ABFE，CDEF 都是边长为1的正方形，则B，D两点间的距离是(　　)‎ 图767‎ A. B. C．1 D. D　[∵＝＋＋，‎ ‎∴||2＝||2＋||2＋||2＋2·＋2·＋2·＝1＋1＋1－＝3－，故||＝.]‎ 二、填空题 ‎6．已知a＝(2,1，－3)，b＝(－1,2,3)，c＝(7,6，λ)，若a，b，c三向量共面，则λ＝________. ‎ ‎【导学号：01772271】‎ ‎－9　[由题意知c＝xa＋yb，‎ 即(7,6，λ)＝x(2,1，－3)＋y(－1,2,3)，‎ ‎∴解得λ＝－9.]‎ ‎7．正四面体ABCD的棱长为2，E，F分别为BC，AD中点，则EF的长为________. ‎ ‎【导学号：01772272】‎ 　[||2＝(＋＋)2‎ ‎＝＋＋＋2(·＋·＋·)‎ ‎＝12＋22＋12＋2(1×2×cos 120°＋0＋2×1×cos 120°)‎ ‎＝2，‎ ‎∴||＝，∴EF的长为.]‎ ‎8．已知O(0,0,0)，A(1,2,3)，B(2,1,2)，P(1,1,2)，点Q在直线OP上运动，当·取最小值时，点Q的坐标是________．‎ 　[由题意，设＝λ，即＝(λ，λ，2λ)，‎ 则＝(1－λ，2－λ，3－2λ)，＝(2－λ，1－λ，2－2λ)，‎ ‎∴·＝(1－λ)(2－λ)＋(2－λ)(1－λ)＋(3－2λ)(2－2λ)＝6λ2－16λ＋10＝62－，当λ＝时有最小值，此时Q点坐标为.]‎ 三、解答题 ‎9．已知空间中三点A(－2,0,2)，B(－1,1,2)，C(－3,0,4)，设a＝，b＝.‎ ‎(1)若|c|＝3，且c∥，求向量c；‎ ‎(2)求向量a与向量b的夹角的余弦值．‎ ‎[解]　(1)∵c∥，＝(－3,0,4)－(－1,1,2)＝(－2，－1,2)，‎ ‎∴c＝m＝m(－2，－1,2)＝(－2m，－m,2m)，2分 ‎∴|c|＝＝3|m|＝3，‎ ‎∴m＝±1.‎ ‎∴c＝(－2，－1,2)或(2,1，－2).5分 ‎(2)∵a＝(1,1,0)，b＝(－1,0,2)．‎ ‎∴a·b＝(1,1,0)·(－1,0,2)＝－1.7分 又∵|a|＝＝，‎ ‎|b|＝＝，‎ ‎∴cos〈a，b〉＝＝＝－，‎ 故向量a与向量b的夹角的余弦值为－.12分 ‎10．(2017·长春模拟)已知空间三点A(0,2,3)，B(－2,1,6)，C(1，－1,5)．‎ ‎(1)求以，为边的平行四边形的面积；‎ ‎(2)若|a|＝，且a分别与，垂直，求向量a的坐标．‎ ‎[解]　(1)由题意可得：＝(－2，－1,3)，＝(1，－3,2)，所以cos〈，〉＝ ‎＝＝＝.3分 所以sin〈，〉＝，‎ 所以以，为边的平行四边形的面积为 S＝2×||·||·sin〈，〉＝14×＝7.5分 ‎(2)设a＝(x，y，z)，由题意得 解得或 所以向量a的坐标为(1,1,1)或(－1，－1，－1).12分 B组　能力提升 ‎(建议用时：15分钟)‎ ‎1．A，B，C，D是空间不共面的四点，且满足·＝0，·＝0，·＝0，M为BC中点，则△AMD是(　　)‎ A．钝角三角形 B．锐角三角形 C．直角三角形 D．不确定 C　[∵M为BC中点，‎ ‎∴＝(＋)，‎ ‎∴·＝(＋)· ‎＝·＋·＝0.‎ ‎∴AM⊥AD，△AMD为直角三角形．]‎ ‎2．已知2a＋b＝(0，－5,10)，c＝(1，－2，－2)，a·c＝4，|b|＝12，则以b，c为方向向量的两直线的夹角为________．‎ ‎60°　[由题意得，(2a＋b)·c＝0＋10－20＝－10.‎ 即2a·c＋b·c＝－10.‎ 又∵a·c＝4，∴b·c＝－18，‎ ‎∴cos〈b，c〉＝＝＝－，‎ ‎∴〈b，c〉＝120°，∴两直线的夹角为60°.]‎ ‎3．在直三棱柱ABCA′B′C′中，AC＝BC＝AA′，∠ACB＝90°，D，E分别为AB，BB′的中点．‎ 图768‎ ‎(1)求证：CE⊥A′D；‎ ‎(2)求异面直线CE与AC′所成角的余弦值. ‎ ‎【导学号：01772273】‎ ‎[解]　(1)证明：设＝a，＝b，＝c，‎ 根据题意得，|a|＝|b|＝|c|，‎ 且a·b＝b·c＝c·a＝0，‎ ‎∴＝b＋c，＝－c＋b－a.3分 ‎∴·＝－c2＋b2＝0.‎ ‎∴⊥，即CE⊥A′D.5分 ‎(2)∵＝－a＋c，||＝|a|，||＝|a|.‎ ·＝(－a＋c)·＝c2＝|a|2，‎ ‎∴cos〈，〉＝＝.10分 即异面直线CE与AC′所成角的余弦值为.12分