辽宁省大连市旅顺口区2018-2019学年高二上学期9月月考数学试卷 8页

‎ 高二数学月考试题 一、选择题：‎ ‎1．若直线过点(,－3)且倾斜角为30°,则该直线的方程为 （ ）‎ A．y＝x－6 B. y＝x＋4 C. y＝x－4 D. y＝x＋2‎ ‎2. 如果A (3, 1)、B (－2, k )、C (8, 11), 在同一直线上，那么k的值是（ ）。‎ A. －6 B. －7 C. －8 D. －9‎ ‎3．下列四个结论：‎ ‎⑴两条直线都和同一个平面平行，则这两条直线平行。‎ ‎⑵两条直线没有公共点，则这两条直线平行。‎ ‎⑶两条直线都和第三条直线垂直，则这两条直线平行。‎ ‎⑷一条直线和一个平面内无数条直线没有公共点，则这条直线和这个平面平行。‎ 其中正确的个数为（ ）‎ A． B． C． D．‎ ‎4.已知直线及平面，下列说法错误的是 （ ） ‎ A．若，，则. B。若，，则.‎ C．若，，则. D。若，，则.‎ ‎5.设变量x、y满足约束条件，则目标函数z=2x+y的最小值为（ ）‎ A.2 B.3 C.４　 　　Ｄ.9‎ ‎6．如图正方体ABCD－A1B1C1D1中，E是AD的中点，则异面直线C1E与BC所成的角的余弦值是 A. B. (　 　)‎ C. D. ‎7．点到直线的距离为（ ） （ D ）‎ ‎ A． B． C． D． ‎ ‎8．已知两条平行直线l1 : 3x＋4y＋2＝0，l2 : 6x＋by＋c＝0间的距离为2，则b＋c＝( )‎ A．12或-48 B．32或-8 C．-32或8 D．－12或48 ‎ ‎9.变量x，y满足约束条件，且有无穷多个点(x，y)使目标函数z＝x＋my取得 最小值，则m＝(　 　)‎ A．－2 B．－1 C．1 D．4‎ ‎10．已知正方体的外接球的体积是，则这个正方体的棱长是(　 　)‎ A. B. C. D. ‎11．在长方体，底面是边长为的正方形，高为，则点到截面的 距离为( ) ‎ A． B． C． D． ‎ ‎12．一个正三棱锥的四个顶点都在半径为1的球面上，其中底面的三个顶点在该球的一个大圆上，则该正三棱锥的体积是 (　　)‎ A. B. C. D. 二、填空题：‎ ‎13．若圆锥的母线长为2 cm，底面圆的周长为2π cm，则圆锥的表面积为________．‎ ‎14.设实数ｘ，ｙ满足，则的最大值是________.‎ ‎15．直二面角－－的棱上有一点，在平面内各有一条射线，‎ 与成，，则 。‎ ‎16．若动点到点和直线的距离相等，则点的轨迹方程为 ‎ 三、解答题 ‎17.已知直线l1：，l2：.求当m为何值时l1与l2 ‎ ‎(1)相交；(2) 平行；(3) 重合（4）垂直.‎ ‎18. 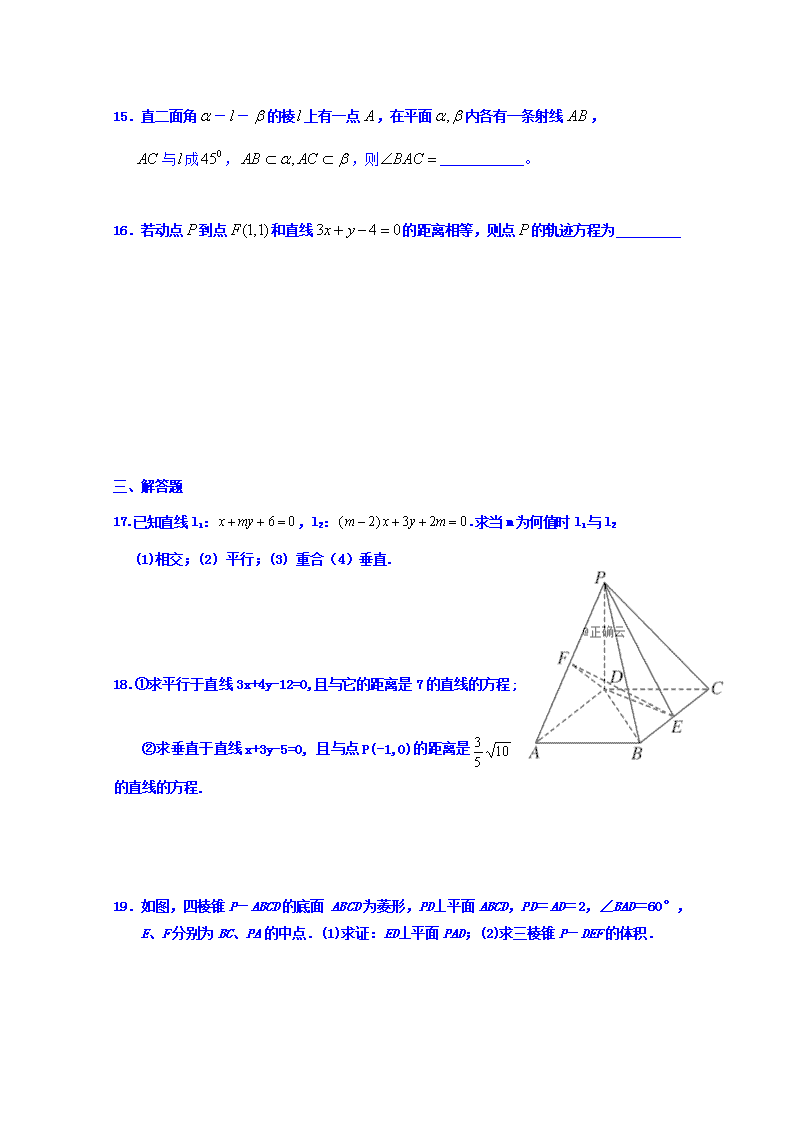①求平行于直线3x+4y-12=0,且与它的距离是7的直线的方程; ‎ ‎ ‎ ‎②求垂直于直线x+3y-5=0, 且与点P(-1,0)的距离是的直线的方程.‎ ‎ ‎ ‎19．如图，四棱锥P－ABCD的底面 ABCD为菱形，PD⊥平面ABCD，PD＝AD＝2，∠BAD＝60°， E、F分别为BC、PA的中点．(1)求证：ED⊥平面PAD；(2)求三棱锥P－DEF的体积．‎ ‎20.已知直线方程为.‎ ‎(1)证明：直线恒过定点； ‎ ‎(2)m为何值时，点Q（3，4）到直线的距离最大，最大值为多少？ ‎ ‎(3)若直线分别与x轴、y轴的负半轴交于A、B两点，求△AOB面积的最小值及此时直线的方程.‎ ‎21.如图, 三棱柱ABC－A1B1C1中, 侧棱A1A⊥底面ABC,且各棱长均相等. D, E, F分别为棱AB, BC, A1C1的中点. ‎ ‎(Ⅰ) 证明EF//平面A1CD; ‎ ‎(Ⅱ) 证明平面A1CD⊥平面A1ABB1; ‎ ‎(Ⅲ) 求直线BC与平面A1CD所成角的正弦值. ‎ ‎22．某家俱公司生产甲、乙两种型号的组合柜，每种柜的制造白坯时间、油漆时间及有关数据如下：‎ ‎　　问该公司如何安排这两种产品的生产，才能获得最大的利润．最大利润是多少？‎ ‎ 高二数学月考试题 一、选择题：CDADBC DBCDCC 二、填空题：‎ ‎13． ___3π___．14. _____.15． 或 。16． ‎ 三、解答题 ‎17.解：（1）相交：且 ‎ （2）平行：‎ ‎ （3）重合：‎ ‎ (4) 垂直：‎ ‎18. ① 或 ‎ ‎②或 ‎ ‎ ‎19．解：(1)证明：连接BD，由已知得BD＝2，‎ 在正三角形BCD中，BE＝EC，‎ ‎∴DE⊥BC，又AD∥BC，‎ ‎∴DE⊥AD.‎ 又PD⊥平面ABCD，‎ ‎∴PD⊥DE，‎ AD∩PD＝D，‎ ‎∴DE⊥平面PAD.‎ ‎(2)∵S△PDF＝·S△PDA＝××22＝1，‎ 且DE＝，‎ ‎∴VP－DEF＝VE－PDF＝·S△PDF·DE＝×1×＝.‎ ‎20.(1) (2) ， (3) ‎ ‎21. (Ⅰ) 略(Ⅱ) 略(Ⅲ) ‎ ‎22．．设x，y分别为甲、乙两种柜的日产量，‎ ‎　　目标函数z=200x＋240y，　线性约束条件：‎ ‎　　　　作出可行域．　　‎ ‎　　 z最大=200×4＋240×8=2720‎ ‎　　答：该公司安排甲、乙两种柜的日产量分别为4台和8台，可获最大利润2720元．‎ ‎　　‎