广西钦州市第三中学2020届高三3月考试数学（理）试题 9页

广西钦州市第三中学2020届高三理数3月份考试试卷 满分：150分 时间：120分钟 姓名： 班级： 考号： ‎ 注意事项：‎ ‎1．答题前填写好自己的姓名、班级、考号等信息 ‎2．请将答案正确填写在答题卡上 第I卷(选择题)‎ 一、单选题(本题共12题，每小题5分，共60分)‎ ‎1．已知集合，，则（ ）‎ A．∅ B． C． D．‎ ‎2．若复数，则（ ）‎ A． B． C． D．‎ ‎3．设，，，则( )‎ A． B． C． D．‎ ‎4．某中学有三栋教学楼，如图所示，若某学生要从处到达他所在的班级处（所有楼道间是连通的），则最短路程不同的走法为（ ）‎ A．5 B．10 C．15 D．20‎ ‎5．已知函数，则其导函数的图象大致是( )‎ A． B． C． D．‎ ‎6．已知倾斜角为的直线过抛物线焦点，且与抛物线相交于两点，若，则（ ）‎ A． B．1 C．2 D．4‎ ‎7．执行如图所示的程序框图，输出的（ ）‎ A．55 B．42 C．33 D．24‎ ‎8．等比数列的前项和为，公比为，若，，则（ ）‎ A． B．2 C． D．3‎ ‎9．如图为某几何体的三视图，则该几何体的外接球的表面积为（ ）‎ A． B． C． D．‎ ‎10.已知双曲线：焦距为，圆：与圆：外切，且的两条渐近线恰为两圆的公切线，则的离心率为（ ）‎ A． B． C． D．‎ ‎11．关于圆周率，数学发展史上出现过许多有创意的求法，如著名的普丰实验和查理斯实验．受其启发，我们也可以通过设计下面的实验来估计的值：先请120名同学每人随机写下一个x，y都小于1的正实数对，再统计其中x，y能与1构成钝角三角形三边的数对的个数m，最后根据统计个数m估计的值．如果统计结果是，那么可以估计的值为（ ）‎ A． B． C． D．‎ ‎12．已知函数在上有两个极值点，则实数的取值范围是（ ）‎ A． B． C． D．‎ 第II卷(非选择题)‎ 二、填空题(本题共4题，每小题5分，共20分)‎ ‎13．已知，则函数的最小值为_______.‎ ‎14．已知，则 ________．‎ ‎15．已知抛物线：（）的焦点为，准线为，过的直线交抛物线于，两点，交于点，若，则________.‎ ‎16．在中，，为边上的点，且，，则面积的最大值为________.‎ 三、解答题(第17题10分，第18-22题每题12分，共70分)‎ ‎17．已知△ABC的内角A，B，C满足．‎ ‎（1）求角A；‎ ‎（2）若△ABC的外接圆半径为1，求△ABC的面积S的最大值．‎ ‎18．已知各项均为正数的数列的前项和满足（）.‎ ‎（1）求数列的通项公式；‎ ‎（2）设，求数列的前项和.‎ ‎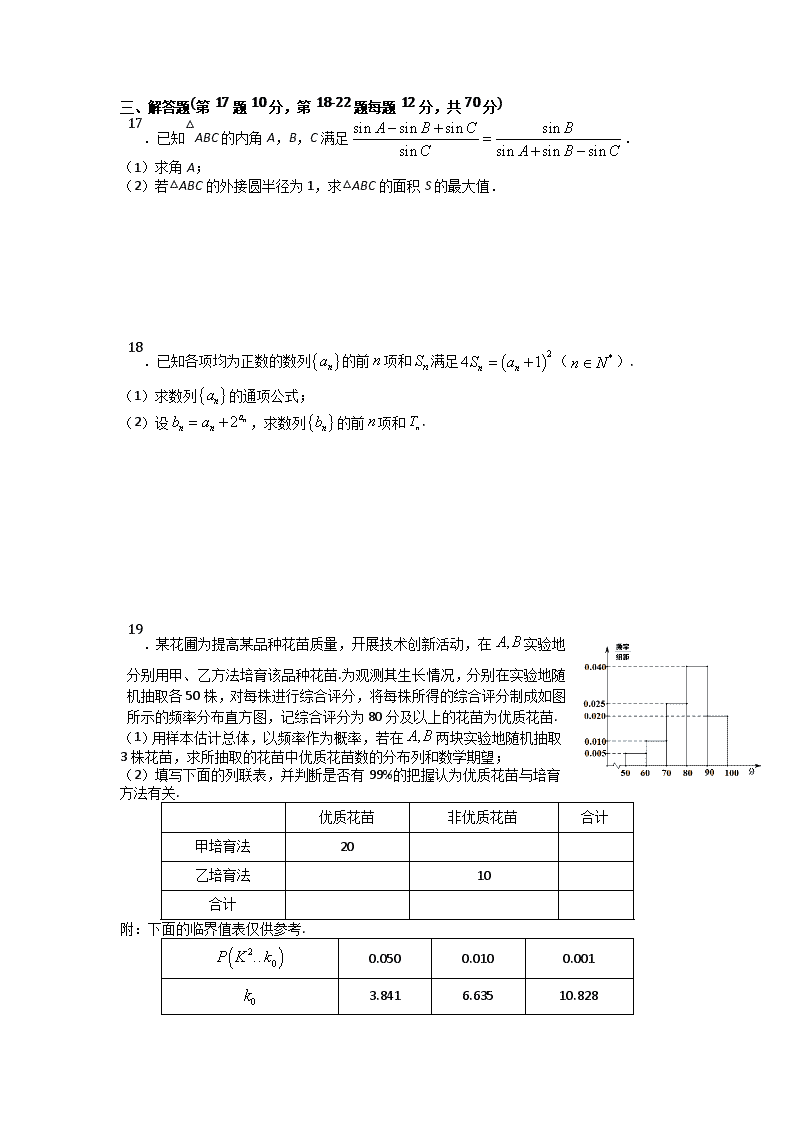19．某花圃为提高某品种花苗质量，开展技术创新活动，在实验地分别用甲、乙方法培育该品种花苗.为观测其生长情况，分别在实验地随机抽取各50株，对每株进行综合评分，将每株所得的综合评分制成如图所示的频率分布直方图，记综合评分为80分及以上的花苗为优质花苗.‎ ‎（1）用样本估计总体，以频率作为概率，若在两块实验地随机抽取3株花苗，求所抽取的花苗中优质花苗数的分布列和数学期望；‎ ‎（2）填写下面的列联表，并判断是否有99%的把握认为优质花苗与培育方法有关.‎ 优质花苗 非优质花苗 合计 甲培育法 ‎20‎ 乙培育法 ‎10‎ 合计 附：下面的临界值表仅供参考.‎ ‎0.050‎ ‎0.010‎ ‎0.001‎ ‎3.841‎ ‎6.635‎ ‎10.828‎ ‎（参考公式：，其中）‎ ‎20.如图，为矩形，且平面平面，，，，，点是线段上的一点，且．‎ ‎（1）证明：；‎ ‎（2）求二面角的余弦值．‎ ‎21．已知定点，，直线、相交于点，且它们的斜率之积为，记动点的轨迹为曲线。‎ ‎（1）求曲线的方程；‎ ‎（2）过点的直线与曲线交于、两点，是否存在定点，使得直线与斜率之积为定值，若存在，求出坐标；若不存在，请说明理由。‎ ‎22．已知函数．‎ ‎（1）讨论函数的单调性；‎ ‎（2）对任意的，恒成立，请求出的取值范围．‎ 参考答案 ‎1．B2．A3．B4．C5．A6．A7．B8．B9．C10．C11．B12．D 13．7 14．243 15．2 16．9‎ ‎ 17．‎ ‎（1）设内角，，所对的边分别为，，．‎ 根据，可得 ‎，‎ 所以，‎ 又因为，所以．‎ ‎（2），‎ 所以，所以（时取等号）．‎ ‎18．‎ ‎（1）由知：当时，有， ，解得 由， 两式相减，得：，化简得：‎ 变形得：，对，有，，即 故 数列是以1为首项，2为公差的等差数列，‎ ‎（2），，‎ ‎ 19．‎ ‎（1）由频率分布直方图可知,优质花苗的频率为,即概率为.‎ 设所抽取的花苗为优质花苗的株数为,则,于是 ‎； ；‎ ‎； .‎ 其分布列为：‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ 所以,所抽取的花苗为优质花苗的数学期望 ‎（2）频率分布直方图,优质花苗的频率为,则样本中优质花苗的株数为60株,列联表如下表所示：‎ 优质花苗 非优质花苗 合计 甲培育法 ‎20‎ ‎30‎ ‎50‎ 乙培育法 ‎40‎ ‎10‎ ‎50‎ 合计 ‎60‎ ‎40‎ ‎100‎ 可得.‎ 所以,有99%的把握认为优质花苗与培育方法有关系 20．（1）证明：由题意知四边形是矩形，是以为直角顶点的等腰直角三角形，且，，，．‎ ‎，．‎ 平面平面，平面平面，，‎ 平面，，‎ ‎，平面．‎ 平面，．‎ ‎（2）解：由（1）知，，两两垂直，‎ 以为原点，，，所在直线分别为，，轴建立如图所示的空间直角坐标系，‎ 则，‎ ‎，.‎ 设平面法向量为，则，‎ 取，则，，故为平面的一个法向量，‎ 易知平面的一个法向量为.‎ 设二面角的平面角为，由题中条件可知，‎ 则，‎ 二面角的余弦值为. 21．（1）设动点，则，‎ ‎，‎ ‎，即，‎ 化简得：。‎ 由已知，故曲线的方程为。‎ ‎（2）由已知直线过点，设的方程为，‎ 则联立方程组，消去得，‎ 设，，则 又直线与斜率分别为，‎ ‎，‎ 则。‎ 当时，，；‎ 当时，，。‎ 所以存在定点，使得直线与斜率之积为定值。 22．解：（1），‎ 若，则，所以函数在上递增；‎ 若，方程的判别式为，‎ 所以方程有两根分别为，，‎ 所以当时，；‎ 当时，，‎ 所以函数在上递减；在上递增.‎ ‎（2）不等式，对任意的恒成立，‎ 即对任意的恒成立．‎ 令，则，‎ 令，则，‎ 易知在上单调递增，‎ 因为，，且的图象在上不间断，‎ 所以存在唯一的，使得，即，则．‎ 当时，单调递减；当时，单调递增．‎ 则在处取得最小值，‎ 且最小值为，‎ 所以，即在上单调递增，所以.‎ 所以． ‎