数学卷·2018届河北省衡水市枣强中学高二上学期第三次月考数学试卷（理科）（解析版） 15页

‎2016-2017学年河北省衡水市枣强中学高二（上）第三次月考数学试卷（理科）‎ ‎　‎ 一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1．已知（x2﹣3x+1）5=a0+a1x+a2x2+…+a10x10，则a1+a2+a3+…+a10=（　　）‎ A．﹣1 B．1 C．﹣2 D．0‎ ‎2．从0，4，6中选两个数字，从3，5，7中选两个数字，组成无重复数字的四位数．其中偶数的个数为（　　）‎ A．56 B．96 C．36 D．360‎ ‎3．从4名男生和3名女生中选出4人参加某个座谈会，若这4人中必须既有男生又有女生，则不同的选法共有（　　）‎ A．140种 B．120种 C．35种 D．34种 ‎4．一条光线从点（﹣2，﹣3）射出，经y轴反射后与圆（x+3）2+（y﹣2）2=1相切，则反射光线所在直线的斜率为（　　）‎ A．﹣或﹣ B．﹣或﹣ C．﹣或﹣ D．﹣或﹣‎ ‎5．投篮测试中，每人投3次，至少投中2次才能通过测试．己知某同学每次投篮投中的概率为0.6，且各次投篮是否投中相互独立，则该同学通过测试的概率为（　　）‎ A．0.648 B．0.432 C．0.36 D．0.312‎ ‎6．若如图的框图所给的程序运行结果为S=20，那么判断框中应填入的关于k的条件是（　　）‎ A．k=9 B．k≤8 C．k＜8 D．k＞8‎ ‎7．如图，已知二面角α﹣PQ﹣β的大小为60°，点C为棱PQ一点，A∈β，AC=2，∠ACP=30°，则点A到平面α的距离为（　　）‎ A．1 B． C． D．‎ ‎8．设实数x，y满足约束条件，则x=x2+y2的最大值为（　　）‎ A． B．68 C． D．32‎ ‎9．的展开式中x的系数是（　　）‎ A．﹣4 B．﹣2 C．2 D．4‎ ‎10．盒子里有形状大小完全相同的3个红球和2个白球，如果不放回的依次取两个球，则在第一次取到白球的条件下，第二次取到红球的概率为（　　）‎ A． B． C． D．‎ ‎11．某车间共有6名工人，他们某日加工零件个数的茎叶图如图所示，其中茎为十位数，叶为个位数，日加工零件个数大于样本均值的工人为优秀工人．从该车间6名工人中，任取2人，则至少有1名优秀工人的概率为 ‎ ‎（　　）‎ A． B． C． D．‎ ‎12．过球面上三点A、B、C的截面和球心的距离是球半径的一半，且AB=6，BC=8，AC=10，则球的表面积是（　　）‎ A．100π B．300π C．π D．π ‎　‎ 二、填空题（每题5分，满分20分，将答案填在答题纸上）‎ ‎13．从区间（0，1）中随机取两个数，则两数之和小于1的概率为　　．‎ ‎14．某城市新修建的一条路上有12盏路灯，为了节省用电而又不能影响正常的照明，可以熄灭其中的三盏灯，但两端的灯不能熄灭，也不能相邻的两盏灯，则熄灭灯的方法有　　种．‎ ‎15．点P在圆C1：（x﹣4）2+（y﹣2）2=9，点Q在圆C2：（x+2）2+（y+1）2=4上，则||的最小值是　　．‎ ‎16．用4种颜色给一个正四面体的4个顶点染色，若同一条棱的两个端点不能用相同的颜色，那么不同的染色方法共有　　种．‎ ‎　‎ 三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）‎ ‎17．某公司进行公开招聘，应聘者从10个考题中通过抽签随机抽取3个题目作答，规定至少答对2道者才有机会进入“面试”环节，小王只会其中的6道．‎ ‎（1）求小王能进入“面试”环节的概率；‎ ‎（2）求抽到小王作答的题目数量的分布列．‎ ‎18．在的展开式中．‎ ‎（1）求二项式系数最大的项；‎ ‎（2）求系数的绝对值最大的项；‎ ‎（3）求系数最小的项．‎ ‎19．一个盒子里装有大小均匀的6个小球，其中有红色球4个，编号分别为1，2，3，4，白色球2个，编号分别为4，5，从盒子中任取3个小球（假设取到任何一个小球的可能性相同）．‎ ‎（1）求取出的3个小球中，含有编号为4的小球的概率；‎ ‎（2）在取出的3个小球中，小球编号的最大值设为X，求随机变量X的分布列．‎ ‎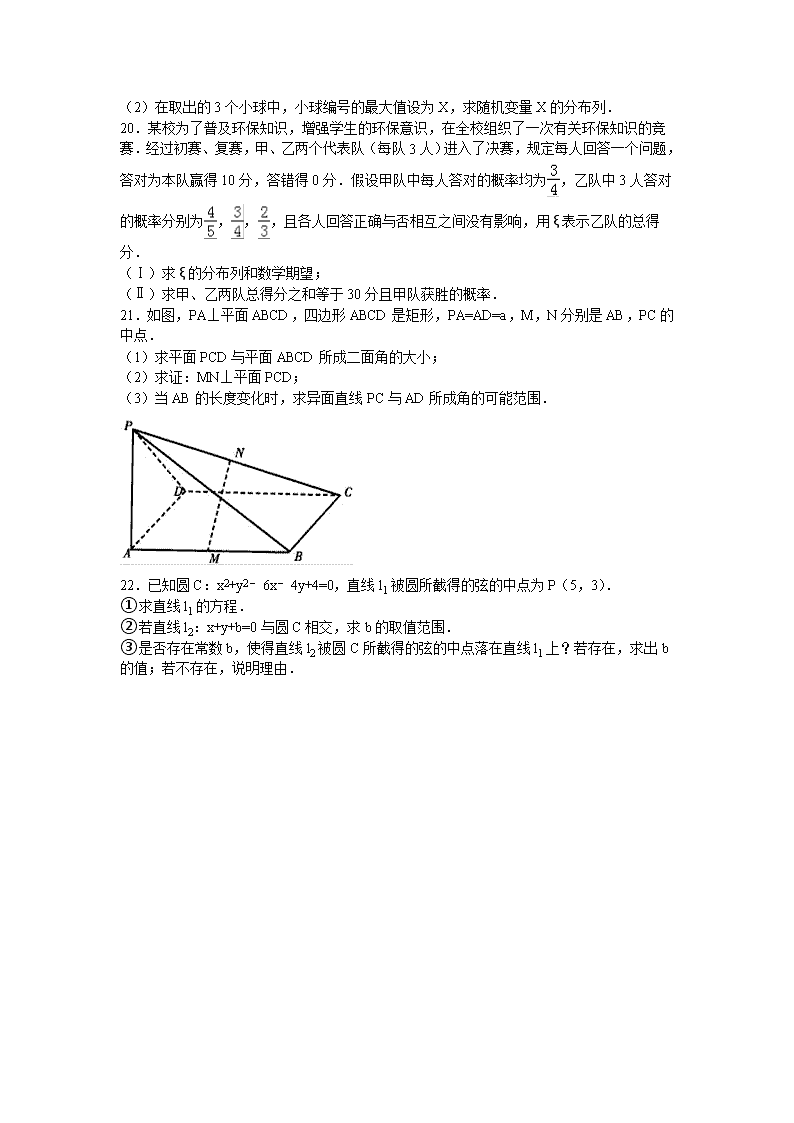20．某校为了普及环保知识，增强学生的环保意识，在全校组织了一次有关环保知识的竞赛．经过初赛、复赛，甲、乙两个代表队（每队3人）进入了决赛，规定每人回答一个问题，答对为本队赢得10分，答错得0分．假设甲队中每人答对的概率均为，乙队中3人答对的概率分别为，，，且各人回答正确与否相互之间没有影响，用ξ表示乙队的总得分．‎ ‎（Ⅰ）求ξ的分布列和数学期望；‎ ‎（Ⅱ）求甲、乙两队总得分之和等于30分且甲队获胜的概率．‎ ‎21．如图，PA⊥平面ABCD，四边形ABCD是矩形，PA=AD=a，M，N分别是AB，PC的中点．‎ ‎（1）求平面PCD与平面ABCD所成二面角的大小；‎ ‎（2）求证：MN⊥平面PCD；‎ ‎（3）当AB的长度变化时，求异面直线PC与AD所成角的可能范围．‎ ‎22．已知圆C：x2+y2﹣6x﹣4y+4=0，直线l1被圆所截得的弦的中点为P（5，3）．‎ ‎①求直线l1的方程．‎ ‎②若直线l2：x+y+b=0与圆C相交，求b的取值范围．‎ ‎③是否存在常数b，使得直线l2被圆C所截得的弦的中点落在直线l1上？若存在，求出b的值；若不存在，说明理由．‎ ‎　‎ ‎2016-2017学年河北省衡水市枣强中学高二（上）第三次月考数学试卷（理科）‎ 参考答案与试题解析 ‎　‎ 一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1．已知（x2﹣3x+1）5=a0+a1x+a2x2+…+a10x10，则a1+a2+a3+…+a10=（　　）‎ A．﹣1 B．1 C．﹣2 D．0‎ ‎【考点】二项式定理的应用．‎ ‎【分析】在所给的等式中，令x=0，可得a0=1，令x=1，可得a0+a1+a2+a3+…+a10=﹣1，由此求得 a1+a2+a3+…+a10的值．‎ ‎【解答】解：由于（x2﹣3x+1）5=a0+a1x+a2x2+…+a10x10，令x=0，可得a0=1，‎ 令x=1，可得a0+a1+a2+a3+…+a10=﹣1，∴a1+a2+a3+…+a10=﹣2，‎ 故选：C．‎ ‎　‎ ‎2．从0，4，6中选两个数字，从3，5，7中选两个数字，组成无重复数字的四位数．其中偶数的个数为（　　）‎ A．56 B．96 C．36 D．360‎ ‎【考点】排列、组合及简单计数问题．‎ ‎【分析】分类讨论，先取奇数，再考虑取偶数，同时分0是否取到，由此可得结论．‎ ‎【解答】解：从3，5，7中选两个数字，共有3种取法 从0，4，6中选两个数字，假设没有取到0，即取4、6，末位是4或6，两种放法，故偶数共有3×2×=36个 假设取到了0，另一个偶数的选取有两种取法，故偶数共有3×2×2×﹣3×2×=60个 故偶数共有36+60=96个 ‎ 故选B．‎ ‎　‎ ‎3．从4名男生和3名女生中选出4人参加某个座谈会，若这4人中必须既有男生又有女生，则不同的选法共有（　　）‎ A．140种 B．120种 C．35种 D．34种 ‎【考点】排列、组合及简单计数问题．‎ ‎【分析】从7个人中选4人共C74种选法，本题不可能只有女生这种情况，去掉不合题意的只有男生的选法C44就可得有既有男生，又有女生的选法．‎ ‎【解答】解：∵7人中任选4人共C74种选法，‎ 去掉只有男生的选法C44，‎ 就可得有既有男生，又有女生的选法C74﹣C44=34．‎ 故选D．‎ ‎　‎ ‎4．一条光线从点（﹣2，﹣3）射出，经y轴反射后与圆（x+3）2+（y﹣2）2=1相切，则反射光线所在直线的斜率为（　　）‎ A．﹣或﹣ B．﹣或﹣ C．﹣或﹣ D．﹣或﹣‎ ‎【考点】圆的切线方程；直线的斜率．‎ ‎【分析】点A（﹣2，﹣3）关于y轴的对称点为A′（2，﹣3），可设反射光线所在直线的方程为：y+3=k（x﹣2），利用直线与圆相切的性质即可得出．‎ ‎【解答】解：点A（﹣2，﹣3）关于y轴的对称点为A′（2，﹣3），‎ 故可设反射光线所在直线的方程为：y+3=k（x﹣2），化为kx﹣y﹣2k﹣3=0．‎ ‎∵反射光线与圆（x+3）2+（y﹣2）2=1相切，‎ ‎∴圆心（﹣3，2）到直线的距离d==1，‎ 化为24k2+50k+24=0，‎ ‎∴k=或﹣．‎ 故选：D．‎ ‎　‎ ‎5．投篮测试中，每人投3次，至少投中2次才能通过测试．己知某同学每次投篮投中的概率为0.6，且各次投篮是否投中相互独立，则该同学通过测试的概率为（　　）‎ A．0.648 B．0.432 C．0.36 D．0.312‎ ‎【考点】n次独立重复试验中恰好发生k次的概率．‎ ‎【分析】判断该同学投篮投中是独立重复试验，然后求解概率即可．‎ ‎【解答】解：由题意可知：同学3次测试满足X∽B（3，0.6），‎ 该同学通过测试的概率为=0.648．‎ 故选：A．‎ ‎　‎ ‎6．若如图的框图所给的程序运行结果为S=20，那么判断框中应填入的关于k的条件是（　　）‎ A．k=9 B．k≤8 C．k＜8 D．k＞8‎ ‎【考点】程序框图．‎ ‎【分析】运行程序框图，确定条件．‎ ‎【解答】解：如图：‎ K ‎10‎ ‎9‎ ‎8‎ s ‎1‎ ‎11‎ ‎20‎ 可知，10，9时条件成立，8时不成立．‎ 故选D．‎ ‎　‎ ‎7．如图，已知二面角α﹣PQ﹣β的大小为60°，点C为棱PQ一点，A∈β，AC=2，∠ACP=30°，则点A到平面α的距离为（　　）‎ A．1 B． C． D．‎ ‎【考点】点、线、面间的距离计算．‎ ‎【分析】过A作AO⊥α于O，点A到平面α的距离为AO；作AD⊥PQ于D，连接OD，说明∠ADO就是二面角α﹣PQ﹣β的大小为60°．‎ 通过三角形ADC与三角形AOD求出AO的值，即可．‎ ‎【解答】解：过A作AO⊥α于O，点A到平面α的距离为AO；‎ 作AD⊥PQ于D，连接OD，‎ 则AD⊥CD，AO⊥OD，∠ADO就是二面角α﹣PQ﹣β的大小为60°．‎ ‎∵AC=2，∠ACP=30°，‎ 所以AD=ACsin30°=2×=1．‎ 在Rt△AOD中，，‎ AO=ADsin60°=1×=．‎ 故答案为：．‎ ‎　‎ ‎8．设实数x，y满足约束条件，则x=x2+y2的最大值为（　　）‎ A． B．68 C． D．32‎ ‎【考点】简单线性规划．‎ ‎【分析】先根据约束条件画出可行域，再利用几何意义求最值，z=x2+y2表示（0，0）到可行域的距离的平方，只需求出（0，0）到可行域的距离的最大值即可．‎ ‎【解答】解：根据约束条件画出可行域 z=x2+y2表示（0，0）到可行域的距离的平方，‎ 当在区域内点A（2，8）时，距离最大，最大距离为 =，‎ 则z=x2+y2的最大值为68．‎ 故选B．‎ ‎　‎ ‎9．的展开式中x的系数是（　　）‎ A．﹣4 B．﹣2 C．2 D．4‎ ‎【考点】组合及组合数公式．‎ ‎【分析】将已知多项式展开，将求展开式中x的项的系数转化为求二项式展开式的项的系数即可．‎ ‎【解答】解：∵（1+2）3的展开式为：1+6+12x+8x，‎ ‎（1﹣）5展开式中x的项的系数是﹣C53=﹣10；常数项为：1‎ ‎∴的展开式中x的系数是：‎ ‎1×（﹣10）+1×12=2．‎ 故选C ‎　‎ ‎10．盒子里有形状大小完全相同的3个红球和2个白球，如果不放回的依次取两个球，则在第一次取到白球的条件下，第二次取到红球的概率为（　　）‎ A． B． C． D．‎ ‎【考点】相互独立事件的概率乘法公式．‎ ‎【分析】在第一次取到白球的条件下，盒子中还有3个红球和一个白球，再利用古典概型及其概率计算公式求得第二次取到红球的概率．‎ ‎【解答】解：在第一次取到白球的条件下，盒子中还有3个红球和一个白球，故第二次取到红球的概率为，‎ 故选：C．‎ ‎　‎ ‎11．某车间共有6名工人，他们某日加工零件个数的茎叶图如图所示，其中茎为十位数，叶为个位数，日加工零件个数大于样本均值的工人为优秀工人．从该车间6名工人中，任取2人，则至少有1名优秀工人的概率为 ‎ ‎（　　）‎ A． B． C． D．‎ ‎【考点】列举法计算基本事件数及事件发生的概率；茎叶图．‎ ‎【分析】由茎叶图可得工人加工的零件数，可得优秀工人数，列举法和概率公式可得．‎ ‎【解答】解：由茎叶图可知6名工人加工零件数为：17，19，20，21，25，30，‎ 平均值为：（17+19+20+21+25+30）=22，优秀的为25，30有2人，‎ 从该车间6名工人中，任取2人共有15种取法：（17，19）（17，20）（17，21）（17，25）（17，30）‎ ‎（19，20）（19，21）（19，25）（19，30）（20，21）（20，25）（20，30）（21，25）（21，30）（25，30）．‎ 其中至少有1名优秀工人的共有9种取法：（17，25）（17，30）（19，25）（19，30）（20，25）（20，30）（21，25）（21，30）（25，30）．‎ 由概率公式可得P==，‎ 故选：C．‎ ‎　‎ ‎12．过球面上三点A、B、C的截面和球心的距离是球半径的一半，且AB=6，BC=8，AC=10，则球的表面积是（　　）‎ A．100π B．300π C．π D．π ‎【考点】球的体积和表面积．‎ ‎【分析】根据边长知△ABC是RT△，则球心的身影为斜边的中点，再由勾股定理求得．‎ ‎【解答】解：根据题意△ABC是RT△，且斜边上的中线为5，‎ 又∵球心的射影为斜边的中点，‎ 设球的半径为r，则有 ‎∴‎ ‎∴‎ 故选D．‎ ‎　‎ 二、填空题（每题5分，满分20分，将答案填在答题纸上）‎ ‎13．从区间（0，1）中随机取两个数，则两数之和小于1的概率为　　．‎ ‎【考点】几何概型．‎ ‎【分析】根据题意，设取出的两个数为x、y，分析可得“0＜x＜1，0＜y＜1”表示的区域为纵横坐标都在（0，1）之间的正方形区域，易得其面积为1，而x+y＜‎ ‎1．表示的区域为直线x+y=1下方，且在0＜x＜1，0＜y＜1所表示区域内部的部分，分别计算其面积，由几何概型的计算公式可得答案．‎ ‎【解答】解：设取出的两个数为x、y；‎ 则有0＜x＜1，0＜y＜1，其表示的区域为纵横坐标都在（0，1）之间的正方形区域，易得其面积为1，‎ 而x+y＜1表示的区域为直线x+y=1下方，且在0＜x＜1，0＜y＜1表示区域内部的部分，如图，‎ 易得其面积为；‎ 则两数之和小于1的概率是 故答案为：‎ ‎　‎ ‎14．某城市新修建的一条路上有12盏路灯，为了节省用电而又不能影响正常的照明，可以熄灭其中的三盏灯，但两端的灯不能熄灭，也不能相邻的两盏灯，则熄灭灯的方法有　56　种．‎ ‎【考点】排列、组合及简单计数问题．‎ ‎【分析】根据题意，先将亮的9盏灯排成一排，分析可得有8个符合条件的空位，用插空法，再将插入熄灭的3盏灯插入8个空位，用组合公式分析可得答案．‎ ‎【解答】解：本题使用插空法，先将亮的9盏灯排成一排，‎ 由题意，两端的灯不能熄灭，则有8个符合条件的空位，‎ 进而在8个空位中，任取3个插入熄灭的3盏灯，‎ 有C83=56种方法，‎ 故答案为56．‎ ‎　‎ ‎15．点P在圆C1：（x﹣4）2+（y﹣2）2=9，点Q在圆C2：（x+2）2+（y+1）2=4上，则||的最小值是　3　．‎ ‎【考点】圆与圆的位置关系及其判定．‎ ‎【分析】分别找出两圆的圆心的坐标，以及半径r和R，利用两点间的距离公式求出两圆心间的距离d，根据d大于两半径之和，得到两圆的位置关系是外离，又P在圆C1上，Q在圆C2上，由d﹣（R+r）即可求出||的最小值．‎ ‎【解答】解：∵圆C1：（x﹣4）2+（y﹣2）2=9的圆心坐标C1（4，2），半径r=3，‎ 圆C2：（x+2）2+（y+1）2=4的圆心坐标C2（﹣2，﹣1），半径R=2，‎ ‎∵d=|C1C2|=＞2+3=R+r，‎ ‎∴两圆的位置关系是外离，‎ 又P在圆C1上，Q在圆C2上，‎ 则||的最小值为d﹣（R+r）=3．‎ 故答案为：3．‎ ‎　‎ ‎16．用4种颜色给一个正四面体的4个顶点染色，若同一条棱的两个端点不能用相同的颜色，那么不同的染色方法共有　24　种．‎ ‎【考点】排列、组合及简单计数问题．‎ ‎【分析】本题相当于将四种元素在四个位置全排列，运用排列数公式计算即可得到所求值．‎ ‎【解答】解：设三棱锥为P﹣ABC．‎ 同一条棱的两个端点不能用相同的颜色，‎ 相当于将四种元素在四个位置全排列，即有A44=24．‎ 故答案为：24．‎ ‎　‎ 三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）‎ ‎17．某公司进行公开招聘，应聘者从10个考题中通过抽签随机抽取3个题目作答，规定至少答对2道者才有机会进入“面试”环节，小王只会其中的6道．‎ ‎（1）求小王能进入“面试”环节的概率；‎ ‎（2）求抽到小王作答的题目数量的分布列．‎ ‎【考点】离散型随机变量及其分布列；古典概型及其概率计算公式．‎ ‎【分析】（1）设小王能进入面试环节为事件A，由互斥事件概率加法公式能求出小王能进入“面试”环节的概率．‎ ‎（2）设抽到小王会作答的题目的数量为x，则x=0，1，2，3，分别求出相应的概率，由此能求出抽到小王作答的题目数量X的分布列．‎ ‎【解答】解：（1）设小王能进入面试环节为事件A，‎ 则P（A）==．‎ ‎（2）设抽到小王会作答的题目的数量为x，则x=0，1，2，3，‎ P（X=0）==，‎ P（X=1）==，‎ P（X=2）==，‎ P（X=3）==，‎ ‎∴抽到小王作答的题目数量X的分布列为：‎ ‎ X ‎ 0‎ ‎ 1‎ ‎ 2‎ ‎3 ‎ ‎ P ‎　‎ ‎18．在的展开式中．‎ ‎（1）求二项式系数最大的项；‎ ‎（2）求系数的绝对值最大的项；‎ ‎（3）求系数最小的项．‎ ‎【考点】二项式定理的应用．‎ ‎【分析】（1）利用二项式系数的性质、二项展开式的通项公式，求得二项式系数最大的项．‎ ‎（2）由条件列出不等式组，求得r的范围，可得结论．‎ ‎（3）利用通项公公式求得系数最小的项．‎ ‎【解答】解：（1）在的展开式中，利用二项式系数的性质可得第五项的二项式系数最大，‎ 该项为．‎ ‎（2）设第r项的系数绝对值最大，即，∴，‎ 从而5≤r≤6，故系数的绝对值最大的项是第6项和第7项.，‎ ‎（3）系数最小的项为第6项：．‎ ‎　‎ ‎19．一个盒子里装有大小均匀的6个小球，其中有红色球4个，编号分别为1，2，3，4，白色球2个，编号分别为4，5，从盒子中任取3个小球（假设取到任何一个小球的可能性相同）．‎ ‎（1）求取出的3个小球中，含有编号为4的小球的概率；‎ ‎（2）在取出的3个小球中，小球编号的最大值设为X，求随机变量X的分布列．‎ ‎【考点】离散型随机变量及其分布列；列举法计算基本事件数及事件发生的概率．‎ ‎【分析】（1）从盒子中任取3个小球，先求出基本事件总数，再求出取出的3个小球中，含有编号为4的小球的基本事件个数，由此能求出取出的3个小球中，含有编号为4的小球的概率．‎ ‎（2）由题意得X的可能取值为3，4，5，分别求出相应的概率，由此能求出随机变量X的分布列．‎ ‎【解答】解：（1）∵一个盒子里装有大小均匀的6个小球，其中有红色球4个，编号分别为1，2，3，4，‎ 白色球2个，编号分别为4，5，从盒子中任取3个小球，‎ 基本事件总数n==20，‎ 取出的3个小球中，含有编号为4的小球的基本事件个数m==16，‎ ‎∴取出的3个小球中，含有编号为4的小球的概率p===．‎ ‎（2）由题意得X的可能取值为3，4，5，‎ P（X=3）==，‎ P（X=4）=+=，‎ P（X=5）==，‎ ‎∴随机变量X的分布列为：‎ ‎ X ‎ 3‎ ‎ 4‎ ‎ 5‎ ‎ P ‎　‎ ‎20．某校为了普及环保知识，增强学生的环保意识，在全校组织了一次有关环保知识的竞赛．经过初赛、复赛，甲、乙两个代表队（每队3人）进入了决赛，规定每人回答一个问题，答对为本队赢得10分，答错得0分．假设甲队中每人答对的概率均为，乙队中3人答对的概率分别为，，，且各人回答正确与否相互之间没有影响，用ξ表示乙队的总得分．‎ ‎（Ⅰ）求ξ的分布列和数学期望；‎ ‎（Ⅱ）求甲、乙两队总得分之和等于30分且甲队获胜的概率．‎ ‎【考点】离散型随机变量的期望与方差；古典概型及其概率计算公式；离散型随机变量及其分布列．‎ ‎【分析】（Ⅰ）由题意知，ξ的可能取值为0，10，20，30，分别求出相应的概率，由此能求出ξ的分布列和Eξ；‎ ‎（Ⅱ）由A表示“甲队得分等于30乙队得分等于0”，B表示“甲队得分等于20乙队得分等于10”，可知A、B互斥．利用互斥事件的概率计算公式即可得出甲、乙两队总得分之和等于30分且甲队获胜的概率．‎ ‎【解答】解：由题意知，ξ的可能取值为0，10，20，30，‎ 由于乙队中3人答对的概率分别为，，，‎ P（ξ=0）=（1﹣）×（1﹣）×（1﹣）=，‎ P（ξ=10）=×（1﹣）×（1﹣）+（1﹣）××（1﹣）+（1﹣）×（1﹣）×==，‎ P（ξ=20）=××（1﹣）+（1﹣）××+×（1﹣）×==，‎ P（ξ=30）=××=，‎ ‎∴ξ的分布列为：‎ ξ ‎0‎ ‎10‎ ‎20‎ ‎30‎ P ‎∴Eξ=0×+10×+20×+30×=．‎ ‎（Ⅱ）由A表示“甲队得分等于30乙队得分等于0”，B表示“甲队得分等于20乙队得分等于10”，可知A、B互斥．‎ 又P（A）==，P（B）=××=，‎ 则甲、乙两队总得分之和等于30分且甲队获胜的概率为 P（A+B）=P（A）+P（B）==．‎ ‎　‎ ‎21．如图，PA⊥平面ABCD，四边形ABCD是矩形，PA=AD=a，M，N分别是AB，PC的中点．‎ ‎（1）求平面PCD与平面ABCD所成二面角的大小；‎ ‎（2）求证：MN⊥平面PCD；‎ ‎（3）当AB的长度变化时，求异面直线PC与AD所成角的可能范围．‎ ‎【考点】与二面角有关的立体几何综合题；异面直线及其所成的角；直线与平面垂直的判定．‎ ‎【分析】（1）由题设条件及几何体的直观图可证得∠PDA是平面PCD与平面ABCD所成二面角的平面角，在Rt△PAD中，求出此角的值即可得到二面角的大小；‎ ‎（2）观察图形，取PD中点E，连接AE，EN，又M，N分别是AB，PC的中点可证得四边形AMNE是平行四边形，得出MN∥AE，再证明AE⊥平面PCD即可得到MN⊥平面PCD；‎ ‎（3）求异面直线所成的角得先作角，由图形及题设条件知∠PCB为异面直线PC，AD所成的角，在三角形PCB中解此角即可；‎ ‎【解答】解：（1）PA⊥平面ABCD，CD⊥AD，∴PD⊥CD．‎ 故∠PDA是平面PCD与平面ABCD所成二面角的平面角．‎ 在Rt△PAD中，PA⊥AD，PA=AD，∴∠PDA=45°．…‎ ‎（2）如图，取PD中点E，连接AE，EN，又M，N分别是AB，PC的中点，‎ ‎∴EN∥CD∥AB∴AMNE是平行四边形∴MN∥AE．‎ 在等腰Rt△PAD中，AE是斜边的中线．∴AE⊥PD．‎ 由PA⊥平面ABCD，四边形ABCD是矩形，可推出CD⊥PD 又CD⊥AD，AD∩PD=D ‎∴CD⊥平面PAD，∴CD⊥AE，‎ 又PD∩CD=D，∴AE⊥平面PCD．∴MN⊥平面PCD．…‎ ‎（3）∵AD∥BC，∴∠PCB为异面直线PC，AD所成的角．‎ 由三垂线定理知PB⊥BC，设AB=x（x＞0）．∴tan∠PCB==．‎ 又∵∈（0，+∞），∴tan∠PCB∈（1，+∞）．‎ 又∠PCB为锐角，∴∠PCB∈（，），‎ 即异面直线PC，AD所成的角的范围为（，）．…‎ ‎　‎ ‎22．已知圆C：x2+y2﹣6x﹣4y+4=0，直线l1被圆所截得的弦的中点为P（5，3）．‎ ‎①求直线l1的方程．‎ ‎②若直线l2：x+y+b=0与圆C相交，求b的取值范围．‎ ‎③是否存在常数b，使得直线l2被圆C所截得的弦的中点落在直线l1上？若存在，求出b的值；若不存在，说明理由．‎ ‎【考点】直线和圆的方程的应用；直线与圆的位置关系．‎ ‎【分析】（1）设直线l1的斜率为则k，由题意可得圆心C（3，2），又弦的中点为P（5，3），可求得kPC=，由k•kPC=﹣1可求k，从而可求直线l1的方程；‎ ‎（2）若直线l2：x+y+b=0与圆C相交，圆心到直线l2的距离小于半径，从而可求得b的取值范围；‎ ‎（3）设直线l2被圆C解得的弦的中点为M（x°，y°），由直线l2与CM垂直，可得x°﹣y°﹣1=0，与x°+y°+b=0联立可求得x0，y0，代入直线l1的方程，求得b，验证即可．‎ ‎【解答】解：①∵圆C的方程化标准方程为：（x﹣3）2+（y﹣2）2=9，‎ ‎∴圆心C（3，2），半径r=3．设直线l1的斜率为则k，则 k=﹣=﹣=﹣2．‎ ‎∴直线l1的方程为：y﹣3=﹣2（x﹣5）即2x+y﹣13=0．‎ ‎②∵圆的半径r=3，‎ ‎∴要使直线l2与圆C相交则须有：＜3，‎ ‎∴|5|＜3于是b的取值范围是：﹣3﹣5＜b＜3﹣5．‎ ‎③设直线l2被圆C解得的弦的中点为M（x°，y°），则直线l2与CM垂直，于是有： =1，‎ 整理可得：x°﹣y°﹣1=0．‎ 又∵点M（x°，y°）在直线l2上，‎ ‎∴x°+y°+b=0；‎ ‎∴由解得：代入直线l1的方程得：1﹣b+﹣13=0，‎ ‎∴b=﹣23∉（﹣3﹣5，3﹣5），‎ 故不存在满足条件的常数b．‎