【数学】2021届一轮复习人教版（文）第7章第1节　不等关系与不等式学案 7页

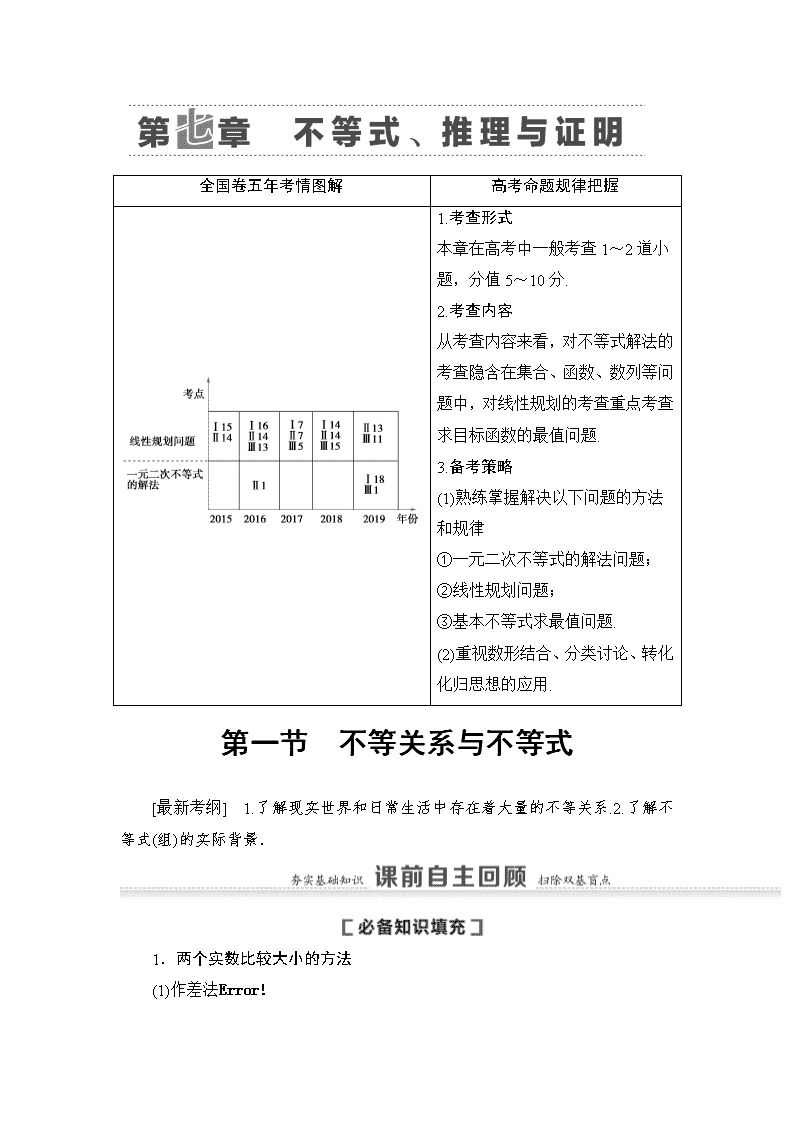
全国卷五年考情图解 高考命题规律把握 ‎1.考查形式 本章在高考中一般考查1～2道小题，分值5～10分.‎ ‎2.考查内容 从考查内容来看，对不等式解法的考查隐含在集合、函数、数列等问题中，对线性规划的考查重点考查求目标函数的最值问题.‎ ‎3.备考策略 ‎(1)熟练掌握解决以下问题的方法和规律 ‎①一元二次不等式的解法问题；‎ ‎②线性规划问题；‎ ‎③基本不等式求最值问题.‎ ‎(2)重视数形结合、分类讨论、转化化归思想的应用.‎ 第一节　不等关系与不等式 ‎[最新考纲]　1.了解现实世界和日常生活中存在着大量的不等关系.2.了解不等式(组)的实际背景．‎ ‎1．两个实数比较大小的方法 ‎(1)作差法 ‎(2)作商法 ‎2．不等式的性质 ‎(1)对称性：a>b⇔bb，b>c⇒a>c；(单向性)‎ ‎(3)可加性：a>b⇔a＋c>b＋c；(双向性)‎ ‎(4)加法法则：a>b，c>d⇒a＋c>b＋d；(单向性)‎ ‎(5)可乘性：a>b，c>0⇒ac>bc；(单向性)‎ a>b，c<0⇒acb>0，c>d>0⇒ac>bd；(单向性)‎ ‎(7)乘方法则：a>b>0⇒an>bn(n≥2，n∈N)；(单向性)‎ ‎(8)开方法则：a>b>0⇒>(n≥2，n∈N)．(单向性)‎ ‎1．倒数性质 ‎(1)a＞b，ab＞0⇒＜；‎ ‎(2)a＜0＜b⇒＜；‎ ‎(3)a＞b＞0，d＞c＞0⇒＞.‎ ‎2．分数性质 若a＞b＞0，m＞0，则 ‎(1)真分数性质：＜；＞(b－m＞0)；‎ ‎(2)假分数性质：＞；＜(b－m＞0)．‎ 一、思考辨析(正确的打“√”，错误的打“×”)‎ ‎(1)若a＞b，则ac2＞bc2. (　　)‎ ‎(2)若ac2＞bc2，则a＞b. (　　)‎ ‎(3)若＞1，则a＞b. (　　)‎ ‎(4)若a＋c＞b＋c，则a＞b. (　　)‎ ‎[答案]　(1)×　(2)√　(3)×　(4)√‎ 二、教材改编 ‎1．设a，b，c∈R，且a＞b，则(　　)‎ A．ac＞bc　　　　　　　 B.＜ C．a2＞b2 D．a3＞b3‎ D　[取a＝1，b＝－2，c＝－1，排除A，B，C，故选D.]‎ ‎2．若a＞b＞0，c＜d＜0，则(　　)‎ A．ad＞bc B．ad＜bc C．ac＞bd D．ac＜bd D　[c＜d＜0⇒－c＞－d＞0，则有－ac＞－bd，所以ac＜bd，故选D.]‎ ‎3．设b＜a，d＜c，则下列不等式中一定成立的是(　　)‎ A．a－c＜b－d B．ac＜bd C．a＋c＞b＋d D．a＋d＞b＋c C　[由a＞b，c＞d得a＋c＞b＋d，故选C.]‎ ‎4．设a＝＋，b＝＋，则a与b的大小关系为(　　)‎ A．a＝b B．a＞b C．a＜b D．无法判断 B　[a2＝17＋2，b2＝17＋2，‎ 由2＞2，知a2＞b2，‎ 又a＞0，b＞0，‎ 所以a＞b，故选B.]‎ 考点1　比较两个数(式)的大小 ‎　比较两个数或代数式的大小的三种方法 ‎(1)当两个数(或式子)正负未知且为多项式时，用作差法．‎ 步骤：①作差；②变形；③判断差的符号；④下结论．‎ 变形技巧：①分解因式；②平方后再作差；③配方；④分子、分母有理化．‎ ‎(2)作商法：适用于分式、指数式、对数式，要求两个数(或式子)为正数．‎ 步骤：①作商；②变形；③判断商与1的大小；④下结论．‎ ‎(3)特殊值法．对于比较复杂的代数式比较大小，利用不等式的性质不易比较大小时，可以采用特殊值法比较．‎ ‎　(1)已知a1，a2∈(0,1)，若M＝a1a2，N＝a1＋a2－1，则M与N的大小关系是(　　)‎ A．M＜N　　　　　　 B．M＞N C．M＝N D．不确定 ‎(2)[一题多解]若a＝，b＝，c＝，则(　　)‎ A．a＜b＜c B．c＜b＜a C．c＜a＜b D．b＜a＜c ‎(1)B　(2)B　[(1)M－N＝a1a2－(a1＋a2－1)＝a1a2－a1－a2＋1＝(a1－1)·(a2－1)．∵a1∈(0,1)，a2∈(0,1)，‎ ‎∴a1－1＜0，a2－1＜0.‎ ‎∴(a1－1)(a2－1)＞0，即M－N＞0.‎ ‎∴M＞N.‎ ‎(2)法一(作商法)：由题意可知a，b，c都是正数．‎ 由＝＝log8164＜1，可知a＞b；‎ 由＝＝log6251 024＞1，可知b＞c.故c＜b＜a.‎ 法二(构造函数法)：令f(x)＝，可得f′(x)＝.易知当x＞e时，f′(x)＜0，即f(x)单调递减，因为e＜3＜4＜5，‎ 所以f(3)＞f(4)＞f(5)，即c＜b＜a.]‎ ‎　本例T(2)也可以用作差法求解．‎ ‎[教师备选例题]‎ 已知等比数列{an}中，a1＞0，q＞0，前n项和为Sn，则与的大小关系为 ．‎ ＜　[当q＝1时，＝3，＝5，‎ 所以＜.‎ 当q＞0且q≠1时，‎ －＝－ ‎＝＝＜0，‎ 所以＜.‎ 综上可知＜.]‎ ‎　1.设M＝2a(a－2)，N＝(a＋1)(a－3)，则有(　　)‎ A．M＞N B．M≥N C．M＜N D．M≤N A　[M－N＝(2a2－4a)－(a2－2a－3)＝a2－2a＋3＝(a－1)2＋2＞0，∴M＞N，故选A.]‎ ‎2．设a，b∈[0，＋∞)，A＝＋，B＝，则A，B的大小关系是(　　)‎ A．A≤B B．A≥B C．A＜B D．A＞B B　[因为A≥0，B≥0，A2－B2＝a＋2＋b－(a＋b)＝2≥0，所以A≥B.故选B.]‎ 考点2　不等式性质的应用(多维探究)‎ ‎1．判断不等式是否成立的方法 ‎(1)直接利用不等式的性质逐个验证，利用不等式的性质判断不等式是否成立时要特别注意前提条件．‎ ‎(2)利用特殊值法排除错误答案．‎ ‎(3)利用函数的单调性，当直接利用不等式的性质不能比较大小时，可以利用指数函数、对数函数、幂函数等函数的单调性进行判断．‎ ‎2．利用不等式的性质求取值范围的方法 由a＜f(x，y)＜b，c＜g(x，y)＜d求F(x，y)的取值范围，可利用待定系数法解决，即设F(x，y)＝mf(x，y)＋ng(x，y)，用恒等变形求得m，n，再利用不等式的性质求得F(x，y)的取值范围．‎ ‎　判断不等式是否成立 ‎　(1)(2019·日照模拟)已知a＞b＞0，c＞1，则下列各式成立的是(　　)‎ A．sin a＞sin b B．ca＞cb C．ac＜bc D.＜ ‎(2)若a＞b＞0，c＜d＜0，则一定有(　　)‎ A.＞ B.＜ C.＞ D.＜ ‎(1)B　(2)B　[(1)对于选项A，若a＝，b＝，则sin a＝sin b，故A选项不成立；‎ 对于选项B，构造函数y＝cx，由于c＞1，故函数y＝cx是增函数，又a＞b＞0，所以ca＞cb，故B选项成立；‎ 对于选项C，构造函数y＝xc，由于c＞1，故函数y＝xc在(0，＋∞)上是增函数，又a＞b＞0，所以ac＞bc，故C选项不成立；‎ 对于选项D，由a＞b＞0得＜，又c－1＞0，所以＜，故D选项不成立．‎ ‎(2)由c＜d＜0得＜＜0，则－＞－＞0，‎ ‎∴－＞－，∴＜，故选B.]‎ ‎　本例两题都可以使用特殊值法求解．‎ ‎　求代数式的取值范围 ‎　(1)已知－1＜x＜4,2＜y＜3，则x－y的取值范围是 ，3x＋2y的取值范围是 ．‎ ‎(2)若－＜α＜β＜，则α－β的取值范围为 ．‎ ‎(1)(－4,2)　(1,18)　(2)(－π，0)　[(1)∵－1＜x＜4,2＜y＜3，‎ ‎∴－3＜－y＜－2，‎ ‎∴－4＜x－y＜2；‎ 由－1＜x＜4,2＜y＜3得 ‎－3＜3x＜12,4＜2y＜6，‎ ‎∴1＜3x＋2y＜18.‎ ‎(2)因为－＜α＜，－＜－β＜，所以－π＜α－β＜π.又α＜β，所以α－β＜0，所以－π＜α－β＜0.]‎ ‎　求解本例T(2)时，易忽视α＜β，从而得到错误答案(－π，π)．‎ ‎　1.如果a＜b＜0，那么下列不等式成立的是(　　)‎ A.＜ B．ab＜b2‎ C．－ab＜－a2 D．－＜－ D　[由a＜b＜0知＞，则－＜－，故选D.]‎ ‎2．已知－1＜x＜y＜3，则x－y的取值范围是 ．‎ ‎(－4,0)　[由－1＜x＜y＜3得，－1＜x＜3，－3＜－y＜1.‎ ‎∴－4＜x－y＜4，又x＜y.‎ 所以x－y＜0.‎ ‎∴－4＜x－y＜0.]‎