2018-2019学年湖北省随州市第二高级中学、郧阳中学高二上学期期中联考数学（文）试题 Word版 8页

随州二中、郧阳中学2017级高二上学期期中考试 数 学（文科）试 卷 Ⅰ卷（选择题，共60分）‎ 一、选择题（本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1．现要完成下列3项抽样调查：①我校共有320名教职工，其中教师270名，行政人员20名，后勤人员30名．为了了解教职工对学校在校务公开方面的意见，拟抽取一个容量为32的样本②学术报告厅有16排，每排有22个座位，有一次报告会恰好坐满了听众，报告会结束后，为了听取意见，需要请16名听众进行座谈③从高二年级24个班级中抽取3个班进行卫生检查．较为合理的抽样方法是( ) ‎ A．①简单随机抽样②系统抽样③分层抽样 B．①简单随机抽样②分层抽样③系统抽样 ‎ C．①系统抽样②简单随机抽样③分层抽样 D．①分层抽样②系统抽样③简单随机抽样 ‎2． 某公司为了增加其商品的销售利润，调查了该商品投入的广告费用x与销售利润y的统计数据如右表,由表中数据得线性回归方程＝x＋，则下列结论中错误的是(　　)‎ 广告费用x(万元)‎ ‎2‎ ‎3‎ ‎5‎ ‎6‎ 销售利润y(万元)‎ ‎5‎ ‎7‎ ‎9‎ ‎11‎ A．>0 B． y与x正相关 C．回归直线过点(4，8) D．＜0 ‎ ‎3．在右图的茎叶图中，甲、乙两组数据的中位数分别是（ ）‎ A．42,42 B．45,46 C．35,42 D．47,48‎ ‎4．在一个袋子中装有分别标注着数字1,2,3,4的四个小球，这些小球除标注的数字外完全相同，现从中随机地一次取出两个小球，则取出的小球标注的数字之和等于6的概率是(　　) ‎ A． B． C． D． ‎ ‎5．直线在轴上截距为，而且它的倾斜角是直线倾斜角的倍，则(　　)‎ A． B．‎ C． D．‎ ‎6．已知两组样本数据的平均数为h，的平均数为k, 则把两组数据合并成一组以后，这组样本的平均数为 (　　)‎ A． B． C． D．‎ ‎7．若圆C经过A(5，2)，B(－1，4)两点，圆心在x轴上，则圆C的方程是(　　)‎ A．(x－2)2＋y2＝13 B．(x＋2)2＋y2＝17 C．(x＋1)2＋y2＝40 D．(x－1)2＋y2＝20‎ ‎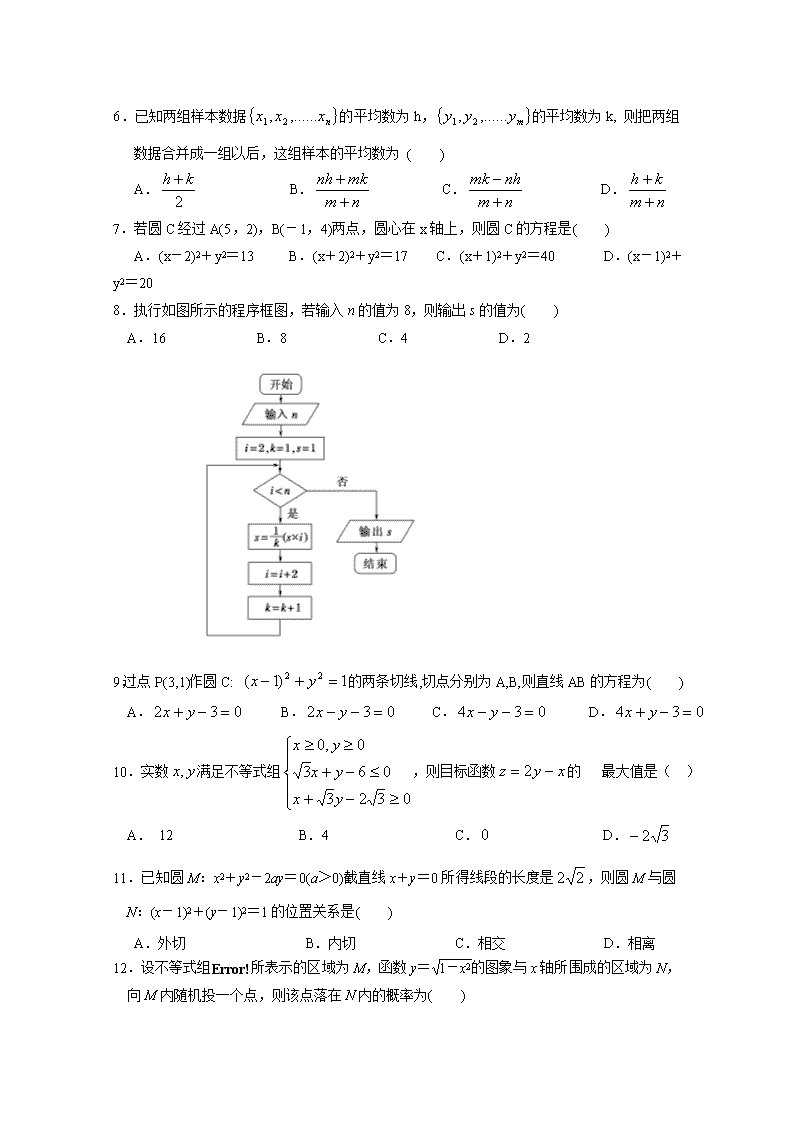8．执行如图所示的程序框图，若输入n的值为8，则输出s的值为(　　)‎ A．16 B．8 C．4 D．2‎ ‎9．过点P(3,1)作圆C: 的两条切线,切点分别为A,B,则直线AB的方程为(　　)‎ A． B． C． D．‎ ‎10．实数满足不等式组，则目标函数的 最大值是（ ）‎ A． 12 B．4 C． D．‎ ‎11．已知圆M：x2＋y2－2ay＝0(a＞0)截直线x＋y＝0所得线段的长度是，则圆M与圆N：(x－1)2＋(y－1)2＝1的位置关系是(　　)‎ A．外切 B．内切 C．相交 D．相离 ‎12．设不等式组所表示的区域为M，函数y＝的图象与x轴所围成的区域为N，向M内随机投一个点，则该点落在N内的概率为(　　)‎ A. B. C. D. Ⅱ卷（非选择题，共90分）‎ 二、填空题（本题共4小题，每小题5分，共20分）‎ ‎13．空间直角坐标系中，在z轴上与点A(－4，1，7)和点B(3，5，－2)等距离的点C的坐标为________．‎ ‎14．将389化成四进位制数的末位是 ．‎ ‎15．福利彩票“双色球”中红色球的号码由编号为01,02，…，33的33个个体组成，某彩民利用下面的随机数表选取6组数作为6个红色球的编号（编号互不相同），选取方法是从随机数表第1行的第6列数字开始由左到右依次选取两个数字，则选出来的第6个红色球的编号为 . ‎ ‎49 54 43 54 82 17 37 93 23 78 87 35 20 96 43 84 26 34 91 64‎ ‎57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76‎ ‎16．将n表示为 （）,当时， ；当时，为0或1．记为上述表示中为1的个数，例如：， ， 故， ， 则 . ‎ 三．解答题（本大题共6小题，共70分．解答应写出文字说明．证明过程或演算步骤）‎ ‎17．(本题满分10分)已知向量 ‎（Ⅰ）若分别表示将一枚质地均匀的骰子先后抛掷两次时第一次、第二次出现的点数，求满足的概率；‎ ‎（Ⅱ）若，求满足的概率．‎ ‎18．（本题满分12分）为了了解高二学生的体能情况，学校抽取部分学生进行一分钟跳绳次数测试，将所得数据整理后，画出频率分布直方图(如图)，图中从左到右各小长方形面积之比为，且第二小组频数为12．‎ ‎（Ⅰ）第二小组的频率是多少？样本容量是多少？‎ ‎（Ⅱ）在这次测试中，学生跳绳次数的中位数落在哪个小组内？请说明理由．‎ ‎（Ⅲ）试估算学生跳绳次数的平均数．‎ ‎19．（本题满分12分）已知圆C： ,‎ 直线 ．‎ ‎（Ⅰ）求证：对任意实数m，直线过定点P,求P的坐标；‎ ‎（Ⅱ）若直线与圆C交于A，B两点，求以线段AB为直径的圆中面积最小的圆的方程．‎ ‎20．(本题满分12分)东风汽车公司生产的“风神”系列轿车有A,B,C三类,每类轿车均有舒适型和标准型两种型号．某周产量如下表:‎ 车型 A B C 舒适 ‎100‎ ‎150‎ 标准 ‎300‎ ‎600‎ 若按分层抽样的方法在这一周生产的轿车中抽取50辆进行检测,则必须抽取A轿车10辆, B轿车15辆． ‎ ‎(Ⅰ)求,的值；‎ ‎(Ⅱ)在年终促销活动中,奖给某优秀销售公司2辆舒适型和3辆标准型C类轿车，该销售公司又从中随机抽取2辆作为奖品回馈消费者，求抽取的这2辆轿车中至少有一辆是舒适型轿车的概率；‎ ‎(Ⅲ)现从A类轿车中抽取8辆,进行能耗等各项指标综合评价,并打分如下：9.4，8.6，9.2，9.6，8.7，9.3，9.0，8.2，求这8个数据的方差． ‎ ‎21．（本题满分12分）兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系，他们记录了本年级1至6月份每月10号的昼夜温差x（℃）与患感冒的人数y（个）的情况，得到如下资料：‎ 日期 ‎1月10日 ‎2月10日 ‎3月10日 ‎4月10日 ‎5月10日 ‎6月10日 昼夜温差x ‎10‎ ‎11‎ ‎13‎ ‎12‎ ‎8‎ ‎6‎ 感冒人数y ‎22‎ ‎25‎ ‎29‎ ‎26‎ ‎16‎ ‎12‎ 该兴趣小组确定的研究方案是：先从这六组数据中选取2组，用剩下的4组数据求线性回归方程，再用被选取的2组数据进行检验．‎ ‎（Ⅰ）求选取的2组数据是不相邻两个月的概率；‎ ‎（Ⅱ）若选取的是1月与6月的两组数据，请用剩下的数据，求出y关于x的线性回归方程；‎ ‎（Ⅲ）若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人，则认为得到的线性回归方程是理想的，试问该小组所得线性回归方程是否理想？‎ 附：回归直线的斜率和截距的估计公式分别为： ‎ ‎22．(本题满分12分) 已知三条直线，直线和直线，且与的距离是.‎ ‎(Ⅰ)求的值；‎ ‎(Ⅱ)能否找到一点，使得点同时满足下列三个条件：①是第一象限的点；②点到的距离是点到的距离的；③点到的距离与点到的距离之比是；若存在，求点坐标；若不存在，说明理由．‎ 高二年级联考文科数学答案 参考答案 一、选择题 DDBCD BDBAA CB 二、填空题 ‎13． 14．1 15．02 16．2]‎ 三．解答题 ‎17．解:（Ⅰ）设表示一个基本事件，则抛掷两次骰子的所有基本事件有（1，1），（1，2），（1，3），（1，4），（1，5），（1，6），（2，1），（2，2），……，（6，5），（6，6）共36个.‎ 用A表示事件“”，即．‎ 则A包含的基本事件有（2，1），（4，2），（6，3），共3个．‎ ‎∴．……………………………………5分 ‎（Ⅱ）用B表示事件“”，即． ‎ 试验的全部结果所构成的区域为 ‎，‎ 构成事件B的区域为 ‎，‎ 如图所示．‎ 所以所求的概率为．……………………………………10分 ‎18．解：(Ⅰ) 由题意知：第二小组的频率为 ‎ 样本容量为； ………………………………4分 ‎（Ⅱ）在频率分布直方图中，中位数左边和右边的直方图面积相等，根据频率分布直方图知，次数在120以下（含120次）的频率为；次数在130以上（含130次）的频率为；‎ ‎∴学生跳绳次数的中位数落在（120，130）内．…………………………8分 ‎（Ⅲ）学生跳绳次数的平均数=+++++‎ ‎=121.8…………………………………10分 ‎19．解：（Ⅰ）直线过定点P（2，2），…………………………………5分 ‎（Ⅱ）圆C：的圆心为C（0，1），半径为，‎ 以线段AB为直径的圆中面积最小时AB⊥CP，P为圆心.‎ 此时由（Ⅰ）知，|CP|=，|PA|=,‎ 所以该圆的方程为…………………………………12分 ‎20．解：(Ⅰ)x=450， y=400………………………………………………………………4分 ‎(Ⅱ)记2辆舒适型轿车为S1,S2,3辆标准型轿车为B1,B2,B3, 设表示一个基本事件,则所有的基本事件数为10个（（S1,S2）,（S1,B1）,（S1,B2）,（S1,B3）,（S2,B1）,（S2,B2）,（S2,B3）,（B1,B2）,（B1,B3）,（B2,B3）），设至少有一辆舒适型轿车记为事件A，事件A发生的基本事件个数为7个（（S1,S2）,（S1,B1）,（S1,B2）,（S1,B3）,（S2,B1）,（S2,B2）,（S2,B3）），‎ 故所求概率为．…………………………………………8分 ‎（Ⅲ）样本的平均数为=9，‎ 则这8个数的方差为 ‎=0.1925……………………………………12分 ‎21．解：（1）……………………………………3分 ‎（Ⅱ）由数据求得,由公式求得,‎ 所以y关于x的线性回归方程为……………………………………8分 ‎（Ⅲ）当时，,‎ 同样，当时，‎ 所以，该小组所得线性回归方程是理想的．……………………………………12分 ‎22解：(Ⅰ)由题意，直线的方程可化为,‎ ‎ ∴与的距离为，‎ 化简得，解得 ‎∴的值为3. ……………………3分 ‎ ‎(Ⅱ)假设存在点满足题设条件，设由①得. （1）‎ 由②得点在两平行直线的平行线上，设的方程为,‎ 则有，‎ 化简得，解得 .……………………5分 ‎ ∴直线的方程为或.‎ ‎∴或. （2） ……………………7分 由③得，化简得.‎ ‎∴. （3） ‎ ‎∵，∴舍去. ……………………10分 由，解得； 舍去 由，解得 ‎∴点即为同时满足三个条件的点． ……………………12分