高一数学教案第8讲：同角三角比的关系 7页

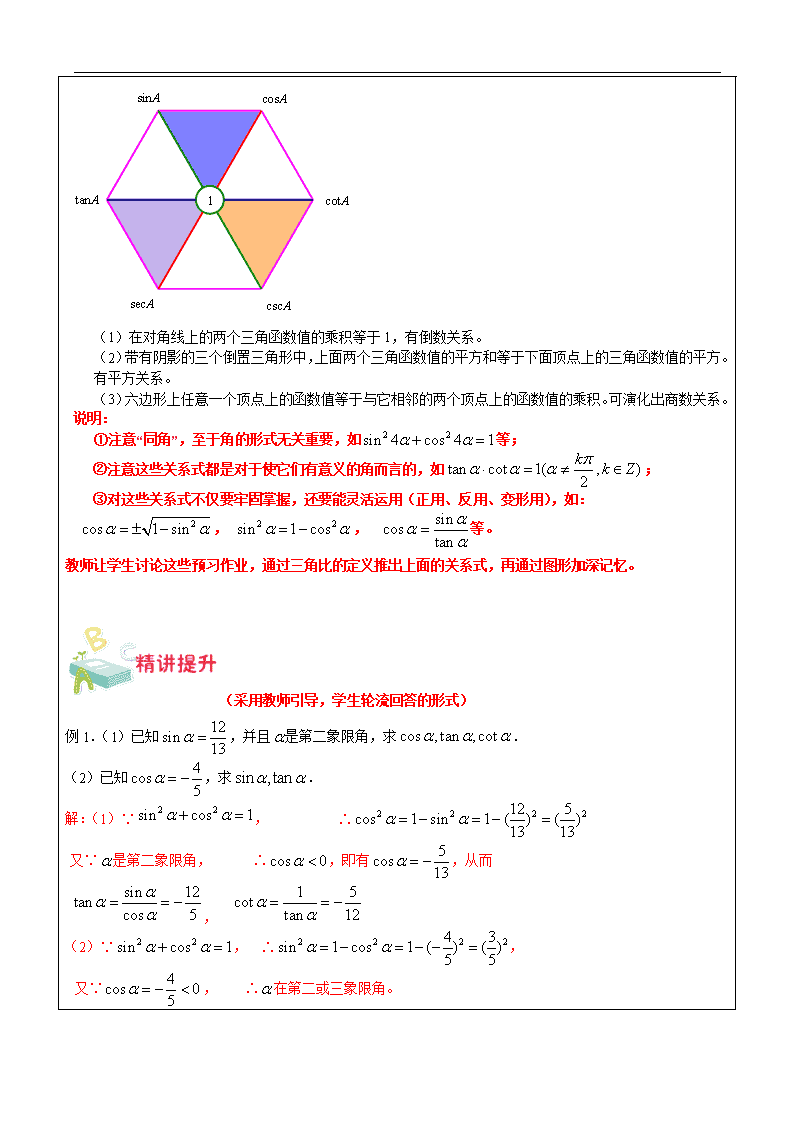
辅导教案 学员姓名： 学科教师：‎ 年 级： 辅导科目： ‎ 授课日期 ‎××年××月××日 ‎ 时 间 A / B / C / D / E / F段 主 题 同角三角比的关系 教学内容 ‎1. 掌握已知一个角的三角比值求其它三角比值的方法。‎ ‎2. 熟练掌握同角三角函数的基本关系式 通过对三角比的定义的学习，试证明下面的关系 ‎（1）倒数关系： （2）商数关系： （3）平方关系：‎ ‎2. 你能说明怎样利用它帮助我们记忆三角函数的基本关系吗？‎ ‎（1）在对角线上的两个三角函数值的乘积等于1，有倒数关系。 （2）带有阴影的三个倒置三角形中，上面两个三角函数值的平方和等于下面顶点上的三角函数值的平方。有平方关系。 （3）六边形上任意一个顶点上的函数值等于与它相邻的两个顶点上的函数值的乘积。可演化出商数关系。‎ 说明：‎ ‎①注意“同角”，至于角的形式无关重要，如等；‎ ‎②注意这些关系式都是对于使它们有意义的角而言的，如；‎ ‎③对这些关系式不仅要牢固掌握，还要能灵活运用（正用、反用、变形用），如：‎ ‎， ， 等。‎ 教师让学生讨论这些预习作业，通过三角比的定义推出上面的关系式，再通过图形加深记忆。‎ ‎（采用教师引导，学生轮流回答的形式）‎ 例1．（1）已知，并且是第二象限角，求．‎ ‎（2）已知，求．‎ 解：（1）∵， ∴‎ 又∵是第二象限角， ∴，即有，从而 ‎， ‎ ‎（2）∵， ∴，‎ 又∵， ∴在第二或三象限角。‎ 当在第二象限时，即有，从而，；‎ 当在第四象限时，即有，从而，．‎ 教师总结：‎ ‎1. 已知一个角的某一个三角函数值，便可运用基本关系式求出其它三角函数值。在求值中，确定角的终边位置是关键和必要的。有时，由于角的终边位置的不确定，因此解的情况不止一种。‎ ‎2. 解题时产生遗漏的主要原因是：①没有确定好或不去确定角的终边位置；②利用平方关系开平方时，漏掉了负的平方根。‎ 试一试：已知 ，求和；‎ 分析:‎ ‎∵,∴‎ ‎∵,∴是第一或第三象限角 当是第一象限角时,‎ 当是第三象限角时,‎ 例2.若，则= .‎ 分析: 原式=‎ ‎【已知正切值时求一些齐次式的结构特点的分式形式的值时可以尝试上下同除某个式子，而、、可以同除】‎ 试一试：已知，求（1）；（2）的值．‎ 分析：（1）；‎ ‎ （2）‎ ‎．‎ 例3. 已知__________‎ 分析：‎ ‎ 两边同时平方，有 ‎ 求出∴.‎ ‎【本题判断三角比的正负值至关重要，没有判断正负会容易出错】‎ 试一试：已知，且．‎ ‎（1）求、的值；‎ ‎（2）求、、的值．‎ 分析：（1）由可得：‎ ‎ ；‎ 于是：，；‎ ‎∵且，∴，．‎ 于是：．‎ ‎（2）；；．‎ ‎（学生统一完成，互相批改，教师针对重难点详细讲解）‎ ‎1. 若sin θ＝－，tan θ>0，则cos θ＝________.‎ 答案：‎ ‎2. 若tan α＝2，则的值为________.‎ 答案：‎ ‎3. 已知，，则＝____‎ 答案：‎ ‎4. 已知，求 ‎ 解：‎ 附加题：求证：．‎ 分析：左边 ‎ 右边．‎ 本节课主要知识点：同角三角比的三种关系的应用 ‎1. 求证：．‎ 证法一：由题义知，所以．‎ ‎∴左边=右边．‎ ‎∴原式成立．‎ 证法二：由题义知，所以．‎ 又∵，‎ ‎∴．‎ 证法三：由题义知，所以．‎ ‎，‎ ‎∴．‎ ‎2. 已知tan α＝2，求sin2α＋sin αcos α－2cos2α；‎ 答案：‎ ‎3. 已知 求 解：∵sin2a + cos2a = 1 ∴‎ 化简，整理得：‎ 当m = 0时，‎ 当m = 8时，‎ 根据三角比的定义，大家不难发现，终边相同的角的同一三角函比值相等，即有： ‎ sin(a+2kπ) = sinα，cos(a+2kπ) = cosα，ta n(a+2kπ) = tanα (k∈Z)‎ 反过来呢？‎ 问题1：你能找出和30°角正弦值相等，但终边不同的角吗？ ‎ 问题2：如果两个角的终边关于x轴对称,你能得出什么结论?两个角的终边关于原点对称呢？‎