数学文·湖南省娄底市双峰一中2017届高三上学期第一次月考数学试卷（文科） Word版含解析 16页

全*品*高*考*网， 用后离不了！2016-2017学年湖南省娄底市双峰一中高三（上）第一次月考数学试卷（文科）‎ ‎　‎ 一、选择题（每小题5分，共60分）‎ ‎1．设A={x|2x＞1}，B={x|y=log2（x+1）}，则A∪B=（　　）‎ A．{x|﹣1＜x＜0} B．{x|x≥1} C．{x|x＞0} D．{x|x＞﹣1}‎ ‎2．设复数z满足=i，则|z|=（　　）‎ A．1 B． C． D．2‎ ‎3．实数a=0.2，b=log0.2，c=的大小关系正确的是（　　）‎ A．a＜c＜b B．a＜b＜c C．b＜a＜c D．b＜c＜a ‎4．已知命题P：“若b2=ac（a，b，c∈R），则a，b，c成等比数列”，q：“函数f（x）=cos（+x）是奇函数”，则下列命题为真命题的是（　　）‎ A．p∨q B．p∧q C．p∨￢q D．￢p∧￢q ‎5．若||=1，||=，且⊥（﹣），则向量，的夹角为（　　）‎ A．45° B．60° C．120° D．135°‎ ‎6．已知m、n是两条不同的直线，α、β是两个不同的平面，给出下列命题：‎ ‎①若α⊥β，m∥α，则m⊥β；‎ ‎②若m⊥α，n⊥β，且m⊥n，则α⊥β；‎ ‎③若m⊥β，m∥α，则α⊥β；‎ ‎④若m∥α，n∥β，且m∥n，则α∥β．‎ 其中正确命题的序号是（　　）‎ A．①④ B．②③ C．②④ D．①③‎ ‎7．在区间[0，4]上随机取两个实数x，y，使得x+2y≤8的概率为（　　）‎ A． B． C． D．‎ ‎8．已知a，b是正实数，则“ab＜3”是“+＞2”的（　　）‎ A．充分不必要条件 B．必要不充分条件 C．既非充分也非必要条件 D．充要条件 ‎9．若某空间几何体的三视图如图所示，则该几何体的体积是（　　）‎ A． B． C．1 D．2‎ ‎10．在△ABC中，a，b，c是角A，B，C的对边，已知bcosC+bsinC﹣a﹣c=0，则角B=（　　）‎ A． B． C． D．‎ ‎11．过双曲线﹣=1（a＞0，b＞0）的一个焦点F作一条渐近线的垂线，垂足为A，与另一条渐近线交于点B，若=2，则此双曲线的离心率为（　　）‎ A． B． C．2 D．‎ ‎12．已知函数f（x）是定义在R上的偶函数，当x≥0时，f（x）=|ex﹣3|，若函数y=f（x）﹣k恰有4 个零点，则实数k的取值范围是（　　）‎ A．（0，ln3） B．（0，2） C．（0，e） D．（0，3）‎ ‎　‎ 二、填空题（每小题5分，共20分）‎ ‎13．函数f（x）=sin（2x﹣），x∈[0，π]的递增区间是　　．‎ ‎14．设等比数列{an}的前n项和为Sn，若27a3﹣a6=0，则=　　．‎ ‎15．已知曲线f（x）=x•lnx在点（1，f（1））处的切线与曲线y=x2+a相切，则a=　　．‎ ‎16．已知函数f（x）=cos2x+2sinx，x∈[0，α]的值域为[1，]，其中α＞0，则角α的取值范围是　　．‎ ‎　‎ 三、解答题（17-21题每小题12分，22题10分．要有必要的文字说明和推理过程）‎ ‎17．已知数列{an}为等差数列，Sn为其前n项和，若a3=20，2S3=S4+8．‎ ‎（1）求数列{an}的通项公式 ‎（2）设bn=（n∈N*），Tn=b1+b2+…+bn，求Tn．‎ ‎18．已知函数f（x）=sinx+cosx（x∈R）．‎ ‎（Ⅰ）若a∈[0，π]且f（a）=2，求a；‎ ‎（Ⅱ）先将y=f（x）的图象上所有点的横坐标缩短到原来的倍（纵坐标不变），再将得到的图象上所有点向右平行移动θ（θ＞0）个单位长度，得到的图象关于直线x=对称，求θ的最小值．‎ ‎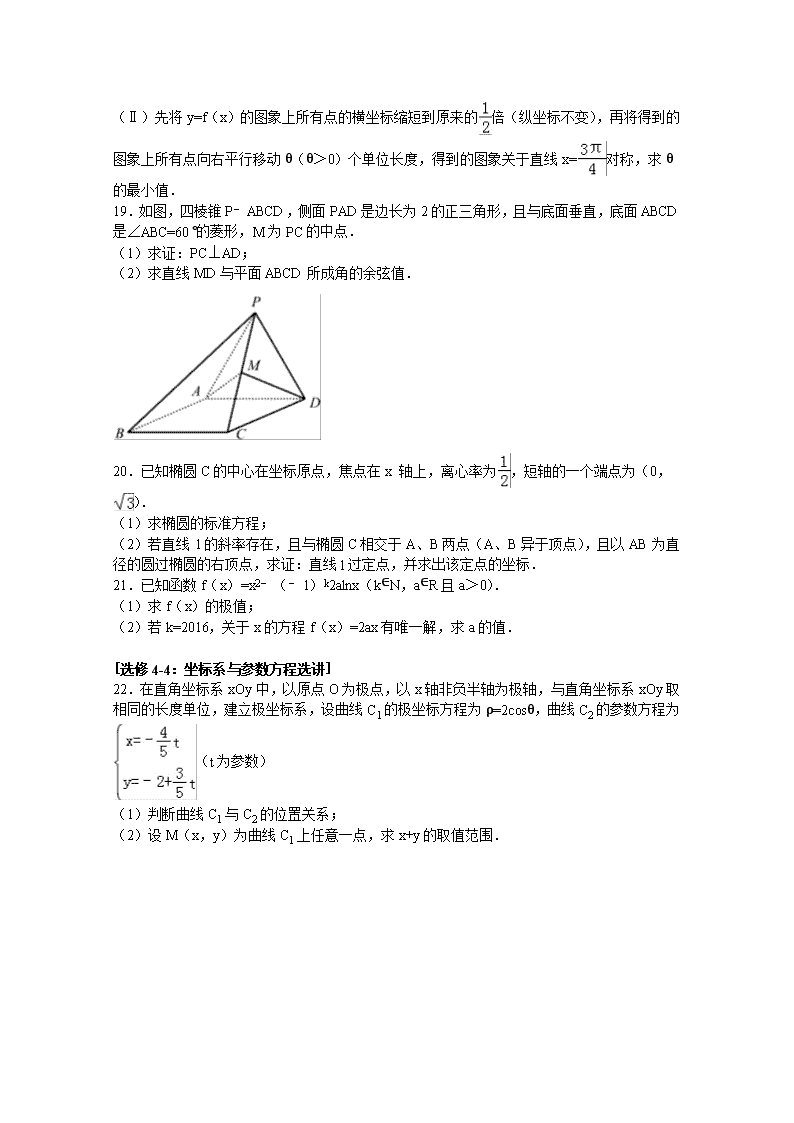19．如图，四棱锥P﹣ABCD，侧面PAD是边长为2的正三角形，且与底面垂直，底面ABCD是∠ABC=60°的菱形，M为PC的中点．‎ ‎（1）求证：PC⊥AD；‎ ‎（2）求直线MD与平面ABCD所成角的余弦值．‎ ‎20．已知椭圆C的中心在坐标原点，焦点在x 轴上，离心率为，短轴的一个端点为（0，）．‎ ‎（1）求椭圆的标准方程；‎ ‎（2）若直线 l的斜率存在，且与椭圆C相交于A、B两点（A、B异于顶点），且以AB为直径的圆过椭圆的右顶点，求证：直线l过定点，并求出该定点的坐标．‎ ‎21．已知函数f（x）=x2﹣（﹣1）k2alnx（k∈N，a∈R且a＞0）．‎ ‎（1）求f（x）的极值；‎ ‎（2）若k=2016，关于x的方程f（x）=2ax有唯一解，求a的值．‎ ‎　‎ ‎[选修4-4：坐标系与参数方程选讲]‎ ‎22．在直角坐标系xOy中，以原点O为极点，以x轴非负半轴为极轴，与直角坐标系xOy取相同的长度单位，建立极坐标系，设曲线C1的极坐标方程为ρ=2cosθ，曲线C2的参数方程为（t为参数）‎ ‎（1）判断曲线C1与C2的位置关系；‎ ‎（2）设M（x，y）为曲线C1上任意一点，求x+y的取值范围．‎ ‎　‎ ‎2016-2017学年湖南省娄底市双峰一中高三（上）第一次月考数学试卷（文科）‎ 参考答案与试题解析 ‎　‎ 一、选择题（每小题5分，共60分）‎ ‎1．设A={x|2x＞1}，B={x|y=log2（x+1）}，则A∪B=（　　）‎ A．{x|﹣1＜x＜0} B．{x|x≥1} C．{x|x＞0} D．{x|x＞﹣1}‎ ‎【考点】并集及其运算．‎ ‎【分析】求出集合A，集合B，然后求解它们的并集即可．‎ ‎【解答】解：因为集合A={x|2x＞1}={x|x＞0}，‎ B={x|y=log2（x+1）}={x|x＞﹣1}，‎ 所以A∪B={x|x＞﹣1}．‎ 故选：D．‎ ‎　‎ ‎2．设复数z满足=i，则|z|=（　　）‎ A．1 B． C． D．2‎ ‎【考点】复数求模．‎ ‎【分析】先化简复数，再求模即可．‎ ‎【解答】解：∵复数z满足=i，‎ ‎∴1+z=i﹣zi，‎ ‎∴z（1+i）=i﹣1，‎ ‎∴z==i，‎ ‎∴|z|=1，‎ 故选：A．‎ ‎　‎ ‎3．实数a=0.2，b=log0.2，c=的大小关系正确的是（　　）‎ A．a＜c＜b B．a＜b＜c C．b＜a＜c D．b＜c＜a ‎【考点】对数函数的图象与性质；指数函数的图象与性质；不等关系与不等式．‎ ‎【分析】根据指数函数，对数函数和幂函数的性质分别判断a，b，c的大小，即可判断．‎ ‎【解答】解：根据指数函数和对数函数的性质，知log0.2＜0，0＜0.2＜1，，‎ 即0＜a＜1，b＜0，c＞1，‎ ‎∴b＜a＜c．‎ 故选：C．‎ ‎　‎ ‎4．已知命题P：“若b2=ac（a，b，c∈R），则a，b，c成等比数列”，q：“函数f（x）=cos（+x）是奇函数”，则下列命题为真命题的是（　　）‎ A．p∨q B．p∧q C．p∨￢q D．￢p∧￢q ‎【考点】复合命题的真假．‎ ‎【分析】分别求出p，q的真假，从而判断出复合命题的真假．‎ ‎【解答】解：对于命题p：若b2=ac，‎ 不妨取a=b=c=0，‎ 显然满足题意，但是不是等比数列，‎ 故该命题为假命题，‎ 对于命题q：“函数f（x）=cos（+x）=﹣sinx是奇函数”，‎ 故命题q是真命题，‎ 故p∨q是真命题，‎ 故选：A．‎ ‎　‎ ‎5．若||=1，||=，且⊥（﹣），则向量，的夹角为（　　）‎ A．45° B．60° C．120° D．135°‎ ‎【考点】数量积表示两个向量的夹角．‎ ‎【分析】设向量的夹角为θ，由=0，可得=1，再利用两个向量的夹角公式求出cosθ，进而求得θ 的值．‎ ‎【解答】解：设向量的夹角为θ，由题意可得==0，可得 ‎=1，即 = cosθ=1×cosθ，‎ 解得 cosθ=．‎ 再由 0≤θ≤π可得θ=，‎ 故选A．‎ ‎　‎ ‎6．已知m、n是两条不同的直线，α、β是两个不同的平面，给出下列命题：‎ ‎①若α⊥β，m∥α，则m⊥β；‎ ‎②若m⊥α，n⊥β，且m⊥n，则α⊥β；‎ ‎③若m⊥β，m∥α，则α⊥β；‎ ‎④若m∥α，n∥β，且m∥n，则α∥β．‎ 其中正确命题的序号是（　　）‎ A．①④ B．②③ C．②④ D．①③‎ ‎【考点】命题的真假判断与应用；空间中直线与平面之间的位置关系．‎ ‎【分析】对于①当α⊥β，m∥α时，m⊥β不一定成立；‎ 对于②可以看成m是平面α的法向量，n是平面β的法向量即可；‎ 对于③可由面面垂直的判断定理作出判断；‎ 对于④m∥α，n∥β，且m∥n，α，β也可能相交．‎ ‎【解答】解：①当α⊥β，m∥α时，m⊥β不一定成立，所以错误；‎ ‎②利用当两个平面的法向量互相垂直时，这两个平面垂直，故成立；‎ ‎③因为m∥α，则一定存在直线n在β，使得m∥n，又m⊥β可得出n⊥β，由面面垂直的判定定理知，α⊥β，故成立；‎ ‎④m∥α，n∥β，且m∥n，α，β也可能相交，如图所示，，所以错误，‎ 故选B．‎ ‎　‎ ‎7．在区间[0，4]上随机取两个实数x，y，使得x+2y≤8的概率为（　　）‎ A． B． C． D．‎ ‎【考点】几何概型．‎ ‎【分析】分别求出在[0，4]上随机取两个实数x，y，x+2y≤8对应的区域，利用面积之比求解即可．‎ ‎【解答】解：由题意，在区间[0，4]上随机取两个实数x，y，对应的区域的面积为16．‎ 在区间[0，4]内随机取两个实数x，y，‎ 则x+2y≤8对应的面积为=12，‎ 所以事件x+2y≤8的概率为=．‎ 故选：D．‎ ‎　‎ ‎8．已知a，b是正实数，则“ab＜3”是“+＞2”的（　　）‎ A．充分不必要条件 B．必要不充分条件 C．既非充分也非必要条件 D．充要条件 ‎【考点】必要条件、充分条件与充要条件的判断．‎ ‎【分析】由a，b是正实数，ab＜3，可得，利用基本不等式的性质可得+≥＞2，反之不成立，例如取a=b=2，即可判断出结论．‎ ‎【解答】解：由a，b是正实数，ab＜3，∴，∴+≥2≥＞2，‎ 反之不成立，例如取a=b=2，‎ ‎∴“ab＜3”是“+＞2”的充分不必要条件，‎ 故选：A．‎ ‎　‎ ‎9．若某空间几何体的三视图如图所示，则该几何体的体积是（　　）‎ A． B． C．1 D．2‎ ‎【考点】由三视图求面积、体积．‎ ‎【分析】几何体的三视图可知几何体是放倒的三棱柱，底面是直角三角形，利用三视图的数据，直接求出棱柱的体积即可．‎ ‎【解答】解：由题意可知几何体的三视图可知几何体是放倒的三棱柱，底面是直角三角形，直角边分别为：1，，棱柱的高为，所以几何体的体积为： =1．‎ 故选C．‎ ‎　‎ ‎10．在△ABC中，a，b，c是角A，B，C的对边，已知bcosC+bsinC﹣a﹣c=0，则角B=（　　）‎ A． B． C． D．‎ ‎【考点】正弦定理．‎ ‎【分析】bcosC+bsinC﹣a﹣c=0，利用正弦定理化简得：sinBcosC+sinBsinC﹣sinA﹣sinC=0，再利用和差公式、诱导公式、三角形内角和定理化简可得： sinB=cosB+1，进而得出．‎ ‎【解答】解：在△ABC中，∵bcosC+bsinC﹣a﹣c=0，‎ 利用正弦定理化简得：sinBcosC+sinBsinC﹣sinA﹣sinC=0，‎ 即sinBcosC+sinBsinC=sinA+sinC=sin（B+C）+sinC=sinBcosC+cosBsinC+sinC=sinBcosC+sinC（cosB+1），‎ ‎∴sinB=cosB+1，即sin（B﹣）=，‎ ‎∵0＜B＜π，∴∈，‎ ‎∴B﹣=，即B=．‎ 故选：B．‎ ‎　‎ ‎11．过双曲线﹣=1（a＞0，b＞0）的一个焦点F作一条渐近线的垂线，垂足为A，与另一条渐近线交于点B，若=2，则此双曲线的离心率为（　　）‎ A． B． C．2 D．‎ ‎【考点】双曲线的简单性质．‎ ‎【分析】先由，得出A为线段FB的中点，再借助于图象分析出其中一条渐近线对应的倾斜角的度数，找到a，b之间的等量关系，进而求出双曲线的离心率．‎ ‎【解答】解：如图因为，所以A为线段FB的中点，‎ ‎∴∠2=∠4，又∠1=∠3，∠2+∠3=90°，所以∠1=∠2+∠4=2∠2=∠3．‎ 故∠2+∠3=90°=3∠2⇒∠2=30°⇒∠1=60°⇒．‎ ‎∴=4⇒e=2．‎ 故选：C．‎ ‎　‎ ‎12．已知函数f（x）是定义在R上的偶函数，当x≥0时，f（x）=|ex﹣3|，若函数y=f（x）﹣k恰有4 个零点，则实数k的取值范围是（　　）‎ A．（0，ln3） B．（0，2） C．（0，e） D．（0，3）‎ ‎【考点】函数奇偶性的性质．‎ ‎【分析】求出f（0）=2，利用函数f（x）是定义在R上的偶函数，函数y=f（x）﹣k恰有4 个零点，即可得出结论．‎ ‎【解答】解：由题意，f（0）=2，‎ ‎∵函数f（x）是定义在R上的偶函数，函数y=f（x）﹣k恰有4 个零点，‎ ‎∴0＜k＜2．‎ 故选：B．‎ ‎　‎ 二、填空题（每小题5分，共20分）‎ ‎13．函数f（x）=sin（2x﹣），x∈[0，π]的递增区间是　，　．‎ ‎【考点】正弦函数的图象．‎ ‎【分析】由﹣+2kπ≤2x﹣≤+2kπ，解得﹣+kπ≤x≤kπ+，（k∈Z），对k取值即可得出．‎ ‎【解答】解：由﹣+2kπ≤2x﹣≤+2kπ，解得﹣+kπ≤x≤kπ+，（k∈Z），‎ 令k=0，可得≤x≤；令k=1，可得≤x≤π+．‎ 又x∈[0，π]，可得函数f（x）的单调递增区间为：，．‎ 故答案为：，．‎ ‎　‎ ‎14．设等比数列{an}的前n项和为Sn，若27a3﹣a6=0，则=　28　．‎ ‎【考点】等比数列的通项公式．‎ ‎【分析】设出等比数列的首项和公比，由已知求出公比，代入等比数列的前n项和得答案．‎ ‎【解答】解：设等比数列{an}的首项为a1，公比为q，‎ 由27a3﹣a6=0，得27a3﹣a3q3=0，即q=3，‎ ‎∴=．‎ 故答案为：28．‎ ‎　‎ ‎15．已知曲线f（x）=x•lnx在点（1，f（1））处的切线与曲线y=x2+a相切，则a=　﹣　．‎ ‎【考点】利用导数研究曲线上某点切线方程．‎ ‎【分析】求出f（x）=x•lnx的导数，求得切线的斜率，可得切线方程，再由于切线与曲线y=x2+a相切，可联立切线与曲线方程，根据△=0得到a的值．‎ ‎【解答】解：f（x）=x•lnx的导数为y′=lnx+1，‎ 曲线f（x）=x•lnx在x=1处的切线斜率为k=1，‎ 则曲线f（x）=x•lnx在点（1，f（1））处的切线方程为y=x﹣1．‎ 由于切线与曲线y=x2+a相切，‎ 故y=x2+a可联立y=x﹣1，‎ 得x2﹣x+a+1=0，‎ 所以有△=1﹣4a﹣4=0，‎ 解得a=﹣．‎ 故答案为：﹣．‎ ‎　‎ ‎16．已知函数f（x）=cos2x+2sinx，x∈[0，α]的值域为[1，]，其中α＞0，则角α的取值范围是　[，π]　．‎ ‎【考点】三角函数中的恒等变换应用；正弦函数的图象．‎ ‎【分析】将函数化简，转化成二次函数问题，求解a的范围即可．‎ ‎【解答】解：由函数f（x）=cos2x+2sinx 可得：f（x）=1﹣2sin2x+2sinx ‎=﹣2（sinx﹣）2+，‎ 对称轴为sinx=，‎ 当sinx=，即x=，f（x）取得最大值为，‎ 故α．‎ 设sinx=t，则0≤t≤1，则x∈[0，π]，‎ 故≤α≤π．‎ 故答案为：[，π]．‎ ‎　‎ 三、解答题（17-21题每小题12分，22题10分．要有必要的文字说明和推理过程）‎ ‎17．已知数列{an}为等差数列，Sn为其前n项和，若a3=20，2S3=S4+8．‎ ‎（1）求数列{an}的通项公式 ‎（2）设bn=（n∈N*），Tn=b1+b2+…+bn，求Tn．‎ ‎【考点】数列的求和；等差数列的通项公式．‎ ‎【分析】（1）运用等差数列的通项公式和求和公式，解方程组，可得首项和公差，即可得到所求通项；‎ ‎（2）求得bn=（﹣），再由数列的求和方法：裂项相消求和，化简整理，即可得到所求和．‎ ‎【解答】解：（1）设数列{an}的公差为d，‎ 由2S3=S4+8得：2（3a1+d）=4a1+d+8，‎ 解得a1=4；‎ 由a3=a1+2d=20，所以d=8，‎ 故数列{an}的通项公式为：an=a1+（n﹣1）d=8n﹣4；‎ ‎（2）由（1）可得，‎ ‎，‎ 则．‎ ‎　‎ ‎18．已知函数f（x）=sinx+cosx（x∈R）．‎ ‎（Ⅰ）若a∈[0，π]且f（a）=2，求a；‎ ‎（Ⅱ）先将y=f（x）的图象上所有点的横坐标缩短到原来的倍（纵坐标不变），再将得到的图象上所有点向右平行移动θ（θ＞0）个单位长度，得到的图象关于直线x=对称，求θ的最小值．‎ ‎【考点】函数y=Asin（ωx+φ）的图象变换．‎ ‎【分析】（Ⅰ）有条阿金利用辅助角公式化简函数f（x）的解析式，再利用f（a）=2，求得a的值．‎ ‎（Ⅱ）根据y=Asin（ωx+φ）的图象变换规律，正弦函数的图象的对称性，求得θ的最小值．‎ ‎【解答】解：（Ⅰ）∵函数f（x）=sinx+cosx=2sin（x+），‎ ‎∵a∈[0，π]，∴a+∈[，]，∵f（a）=2sin（a+）=2，‎ ‎∴sin（a+）=，∴a+=，∴a=．‎ ‎（Ⅱ）先将y=f（x）的图象上所有点的横坐标缩短到原来的倍（纵坐标不变），‎ 得到 y=2sin（2x+）的图象；‎ 再将得到的图象上所有点向右平行移动θ（θ＞0）个单位长度，得到y=2sin（2x﹣2θ+）的图象，‎ 再结合得到的图象关于直线x=对称，可得﹣2θ+=kπ+，‎ 求得θ=﹣，k∈Z，故θ的最小值为．‎ ‎　‎ ‎19．如图，四棱锥P﹣ABCD，侧面PAD是边长为2的正三角形，且与底面垂直，底面ABCD是∠ABC=60°的菱形，M为PC的中点．‎ ‎（1）求证：PC⊥AD；‎ ‎（2）求直线MD与平面ABCD所成角的余弦值．‎ ‎【考点】直线与平面所成的角；空间中直线与直线之间的位置关系．‎ ‎【分析】（1）取AD的中点O，连结OP，OC，证明AD⊥平面OPC即可得出PC⊥AD；‎ ‎（2）取OC的中点N，连结MN，DN，可证MN⊥平面ABCD，故而∠MDN为DM与平面ABCD所成的角，利用勾股定理计算DN，DM得出cos∠MDN．‎ ‎【解答】解：（1）取AD的中点O，连结OP，OC，‎ ‎∵底面ABCD是∠ABC=60°的菱形，‎ ‎∴△ACD是等边三角形，‎ 又侧面PAD是边长为2的正三角形，O为AD的中点，‎ ‎∴OP⊥AD，OC⊥AD，‎ 又OP⊂平面OPC，OC⊂平面OPC，OP∩OC=O，‎ ‎∴AD⊥平面OPC，又PC⊂平面OPC，‎ ‎∴AD⊥PC．‎ ‎（2）取OC的中点N，连结MN，DN，‎ ‎∵平面PAD⊥平面ABCD，平面PAD∩平面ABCD=AD，OP⊥AD，‎ ‎∴OP⊥平面ABCD，‎ ‎∵M，N分别是PC，OC的中点，‎ ‎∴MN∥PO，‎ ‎∴MN⊥平面ABCD，‎ ‎∴∠MDN为DM与平面ABCD所成的角，‎ ‎∵△APD，△ACD是边长为2的等边三角形，‎ ‎∴OC=OP=，OD=1，∴MN=ON=，‎ ‎∴DN==，∴DM==．‎ ‎∴cos∠MDN==．‎ ‎　‎ ‎20．已知椭圆C的中心在坐标原点，焦点在x 轴上，离心率为，短轴的一个端点为（0，）．‎ ‎（1）求椭圆的标准方程；‎ ‎（2）若直线 l的斜率存在，且与椭圆C相交于A、B两点（A、B异于顶点），且以AB为直径的圆过椭圆的右顶点，求证：直线l过定点，并求出该定点的坐标．‎ ‎【考点】椭圆的简单性质．‎ ‎【分析】（1）由e==，即a=2c，b=，根据椭圆的性质，即可求得a和c的值，求得椭圆的标准方程；‎ ‎（2）将直线l的方程与椭圆的方程联立可得根与系数的关系，再利用以AB为直径的圆过椭圆的右顶点D，可得kAD•kBD=﹣1，即可得出m与k的关系，从而得出答案．‎ ‎【解答】解：（1）由题意可知：设椭圆方程为：（a＞b＞0），‎ e==，即a=2c，b=，‎ 由a2=b2+c2，解得：a=2，c=1，‎ 椭圆的标准方程为；‎ ‎（2）设直线l的方程为y=kx+m，A（x1，y1），B（x2，y2），右顶点为D，‎ 由得（3+4k2）x2+8mkx+4（m2﹣3）=0，‎ ‎△=64m2k2﹣16（3+4k2）（m2﹣3）＞0，化为3+4k2＞m2．‎ ‎∴x1+x2=，x1•x2=，‎ y1y2=（kx1+m）（kx2+m）=k2x1•x2+mk（x1+x2）+m2=，‎ ‎∵以AB为直径的圆过椭圆的右顶点D（2，0），kAD•kBD=﹣1，‎ ‎∴•=﹣1，‎ ‎∴y1y2+x1x2﹣2（x1+x2）+4=0，‎ ‎∴+++4=0．‎ 化为7m2+16mk+4k2=0，解得m1=﹣2k，m2=﹣，‎ 当m1=﹣2k，时，直线l的方程为y=k（x﹣2），直线过定点（2，0）矛盾；‎ 当m2=﹣时，直线l的方程为y=k（x﹣），直线过定点（，0）．‎ ‎∴直线过定点（，0）．‎ ‎　‎ ‎21．已知函数f（x）=x2﹣（﹣1）k2alnx（k∈N，a∈R且a＞0）．‎ ‎（1）求f（x）的极值；‎ ‎（2）若k=2016，关于x的方程f（x）=2ax有唯一解，求a的值．‎ ‎【考点】利用导数研究函数的极值．‎ ‎【分析】（1）求出函数的导数，通过k为偶数与奇数，求解函数的极值即可．‎ ‎（2）k=2016，化简关于x的方程f（x）=2ax，构造函数g（x）=x2﹣2alnx﹣2ax，求出函数的导数，求出极值点，判断函数的单调性，利用函数的零点个数，求解即可．‎ ‎【解答】解：（1）函数f（x）=x2﹣（﹣1）k2alnx（k∈N，a∈R且a＞0）．‎ 可得，‎ 当k为奇数时，，∴f（x）在（0，+∞）上单调递增，f（x）无极值．‎ 当k为偶数时，，‎ ‎∴f（x）在上单调递减，上单调递增，‎ ‎∴f（x）有极小值，…‎ ‎（2）∵k=2016，则f（x）=x2﹣2alnx，‎ 令g（x）=x2﹣2alnx﹣2ax，‎ 令g′（x）=0，∴x2﹣ax﹣a=0，∵a＞0，x＞0，∴．‎ 当x∈（0，x0）时，g′（x）＜0，∴g（x）在（0，x0）上单调递减．‎ 当x∈（x0，+∞）时，g′（x）＞0，∴g（x）在（x0，+∞）上单调递增…‎ 又g（x）=0有唯一解，∴，即…‎ ‎②﹣①得：2alnx0+ax0﹣a=0⇒2lnx0+x0﹣1=0⇒x0=1．‎ ‎∴12﹣a﹣a=0．‎ ‎∴…‎ ‎　‎ ‎[选修4-4：坐标系与参数方程选讲]‎ ‎22．在直角坐标系xOy中，以原点O为极点，以x轴非负半轴为极轴，与直角坐标系xOy取相同的长度单位，建立极坐标系，设曲线C1的极坐标方程为ρ=2cosθ，曲线C2的参数方程为（t为参数）‎ ‎（1）判断曲线C1与C2的位置关系；‎ ‎（2）设M（x，y）为曲线C1上任意一点，求x+y的取值范围．‎ ‎【考点】参数方程化成普通方程；简单曲线的极坐标方程．‎ ‎【分析】（1）曲线C1与C2，化为普通方程，即可判断曲线C1与C2的位置关系；‎ ‎（2）令t=x+y，即x+y﹣t=0，利用圆心到直线的距离d=≤1，求出t的范围，即可求x+y的取值范围．‎ ‎【解答】解：（1）曲线C1的极坐标方程为ρ=2cosθ，所以C1的普通方程为（x﹣1）2+y2=1，‎ 曲线C2的参数方程为（t为参数），所以C2的普通方程为3x+4y+8=0，‎ 圆心C1（1，0）到3x+4y+8=0的距离d=＞1，‎ 所以C1与C2相离．‎ ‎（2）令t=x+y，即x+y﹣t=0，‎ 圆心到直线的距离d=≤1，‎ ‎∴1﹣≤t≤1+，‎ ‎∴x+y的取值范围是[1﹣，1+]．‎ ‎　‎ ‎2016年11月8日