2019届二轮复习(文)2-6-2-2统计与概率课件（33张） 33页

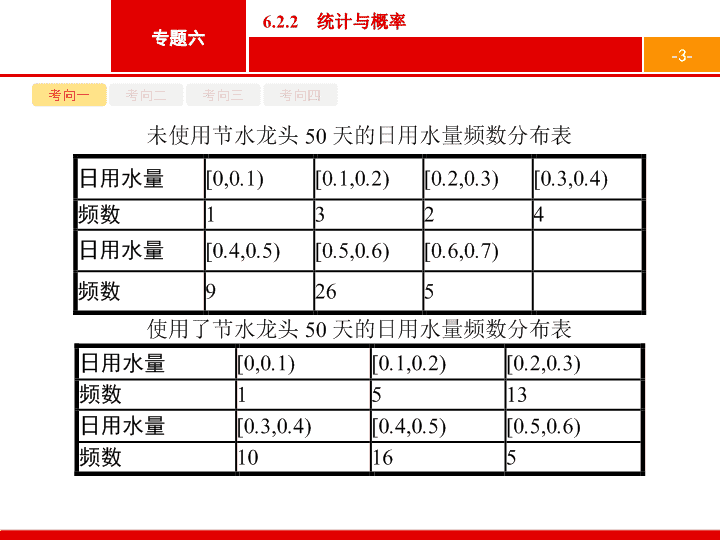
6.2.2 　统计与概率 - 2 - 考向一 考向二 考向三 考 向 四 频率分布表 ( 图 ) 与概率的综合 例 1 (2018 全国卷 1, 文 19) 某家庭记录了未使用节水龙头 50 天的日用水量数据 ( 单位 :m 3 ) 和使用了节水龙头 50 天的日用水量数据 , 得到频数分布表如下 : - 3 - 考向一 考向二 考向三 考 向 四 - 4 - 考向一 考向二 考向三 考 向 四 (1) 作出使用了节水龙头 50 天的日用水量数据的频率分布直方图 : ( 2) 估计该家庭使用节水龙头后 , 日用水量小于 0 . 35 m 3 的概率 ; (3) 估计该家庭使用节水龙头后 , 一年能节省多少水 ?( 一年按 365 天计算 , 同一组中的数据以这组数据所在区间中点的值作代表 . ) - 5 - 考向一 考向二 考向三 考 向 四 解 (1 ) - 6 - 考向一 考向二 考向三 考 向 四 (2) 根据以上数据 , 该家庭使用节水龙头后 50 天日用水量小于 0 . 35 m 3 的频率为 0 . 2 × 0 . 1 + 1 × 0 . 1 + 2 . 6 × 0 . 1 + 2 × 0 . 05 = 0 . 48, 因此该家庭使用节水龙头后日用水量小于 0 . 35 m 3 的概率的估计值为 0 . 48 . (3) 该家庭未使用节水龙头 50 天日用水量的平均数 为 - 7 - 考向一 考向二 考向三 考 向 四 解题心得 在统计中 , 若事件发生的概率无法求出 , 则可以通过计算现实生活中该事件发生的频率来代替概率 . - 8 - 考向一 考向二 考向三 考 向 四 对点训练 1 某超市计划按月订购一种酸奶 , 每天进货量相同 , 进货成本每瓶 4 元 , 售价每瓶 6 元 , 未售出的酸奶降价处理 , 以每瓶 2 元的价格当天全部处理完 . 根据往年销售经验 , 每天需求量与当天最高气温 ( 单位 : ℃ ) 有关 . 如果最高气温不低于 25, 需求量为 500 瓶 ; 如果最高气温位于区间 [20,25), 需求量为 300 瓶 ; 如果最高气温低于 20, 需求量为 200 瓶 . 为了确定六月份的订购计划 , 统计了前三年六月份各天的最高气温数据 , 得下面的频数分布表 : - 9 - 考向一 考向二 考向三 考 向 四 以最高气温位于各区间的频率估计最高气温位于该区间的概率 . (1) 估计六月份这种酸奶一天的需求量不超过 300 瓶的概率 ; (2) 设六月份一天销售这种酸奶的利润为 Y ( 单位 : 元 ), 当六月份这种酸奶一天的进货量为 450 瓶时 , 写出 Y 的所有可能值 , 并估计 Y 大于零的概率 . 解 (1) 这种酸奶一天的需求量不超过 300 瓶 , 当且仅当最高气温低于 25, 由表格数据知 , 最高气温低于 25 的频率 为 所以 这种酸奶一天的需求量不超过 300 瓶的概率的估计值为 0 . 6 . - 10 - 考向一 考向二 考向三 考 向 四 ( 2) 当这种酸奶一天的进货量为 450 瓶时 , 若最高气温不低于 25, 则 Y= 6 × 450 - 4 × 450 = 900; 若最高气温位于区间 [20,25), 则 Y= 6 × 300 + 2(450 - 300) - 4 × 450 = 300; 若最高气温低于 20, 则 Y= 6 × 200 + 2(450 - 200) - 4 × 450 =- 100 . 所以 , Y 的所有可能值为 900,300, - 100 . Y 大于零当且仅当最高气温不低于 20, 由表格数据知 , 最高气温 不 因此 Y 大于零的概率的估计值为 0 . 8 . - 11 - 考向一 考向二 考向三 考 向 四 抽样与古典概型的综合 例 2 (2018 天津卷 , 文 15) 已知某校甲、乙、丙三个年级的学生志愿者人数分别为 240,160,160 . 现采用分层抽样的方法从中抽取 7 名同学去某敬老院参加献爱心活动 . (1) 应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人 ? (2) 设抽出的 7 名同学分别用 A,B,C,D,E,F,G 表示 , 现从中随机抽取 2 名同学承担敬老院的卫生工作 . ① 试用所给字母列举出所有可能的抽取结果 ; ② 设 M 为事件 “ 抽取的 2 名同学来自同一年级 ”, 求事件 M 发生的概率 . - 12 - 考向一 考向二 考向三 考 向 四 解 (1) 由已知 , 甲、乙、丙三个年级的学生志愿者人数之比为 3 ∶ 2 ∶ 2, 由于采用分层抽样的方法从中抽取 7 名同学 , 因此应从甲、乙、丙三个年级的学生志愿者中分别抽取 3 人 ,2 人 ,2 人 . (2) ① 从抽出的 7 名同学中随机抽取 2 名同学的所有可能结果为 {A,B},{A,C},{A,D},{A,E},{A,F},{A,G},{B,C},{B,D},{B,E},{B,F},{B,G},{C,D},{C,E},{C,F},{C,G},{D,E},{D,F},{D,G},{E,F},{E,G},{F,G}, 共 21 种 . ② 由 (1), 不妨设抽出的 7 名同学中 , 来自甲年级的是 A,B,C, 来自乙年级的是 D,E, 来自丙年级的是 F,G, 则从抽出的 7 名同学中随机抽取的 2 名同学来自同一年级的所有可能结果为 {A,B},{A,C},{B,C},{D,E},{F,G}, 共 5 种 . 所以 , 事件 M 发生的概率 P ( M ) = - 13 - 考向一 考向二 考向三 考 向 四 解题心得 解决抽样与古典概型的综合问题的方法 :(1) 定数 , 利用统计知识确定频数 ;(2) 定型 , 根据事件 “ 有限性和等可能性 ” 判断是否为古典概型 ;(3) 定性 , 由题意用列举的方法确定试验的基本事件总数和某事件所含的基本事件数 ;(4) 代入公式求解 . - 14 - 考向一 考向二 考向三 考 向 四 对点训练 2 (2018 江西南昌三模 , 文 19) 十九大提出 : 坚决打赢脱贫攻坚战 , 做到精准扶贫 , 某帮扶单位为帮助定点扶贫村真正脱贫 , 坚持扶贫同扶智相结合 , 帮助贫困村种植蜜柚 , 并利用互联网电商渠道进行销售 . 为了更好地销售 , 现从该村的蜜柚树上随机摘下了 100 个蜜柚进行测重 , 其质量分布在区间 [1 500,3 000] 内 ( 单位 : 克 ), 统计质量的数据 , 作出其频率分布直方图如图所示 : - 15 - 考向一 考向二 考向三 考 向 四 (1) 按分层抽样的方法从质量落在 [1 750,2 000),[2 000,2 250) 的蜜柚中随机抽取 5 个 , 再从这 5 个蜜柚中随机抽 2 个 , 求这 2 个蜜柚质量均小于 2 000 克的概率 ; (2) 以各组数据的中间数值代表这组数据的平均水平 , 以频率代表概率 , 已知该贫困村的蜜柚树上大约还有 5 000 个蜜柚待出售 , 某电商提出两种收购方案 : A. 所有蜜柚均以 40 元 / 千克收购 ; B. 低于 2 250 克的蜜柚以 60 元 / 个收购 , 高于或等于 2 250 的以 80 元 / 个收购 . 请你通过计算为该村选择收益最好的方案 . - 16 - 考向一 考向二 考向三 考 向 四 解 (1) 由题得蜜柚质量在 [1 750,2 000) 和 [2 000,2 250) 的比例为 2 ∶ 3, 故应分别在质量为 [1 750,2 000) 和 [2 000,2 250) 的蜜柚中各抽取 2 个和 3 个 . 记抽取质量在 [1 750,2 000) 的蜜柚为 A 1 , A 2 , 质量在 [2 000,2 250) 的蜜柚为 B 1 , B 2 , B 3 , 则从这 5 个蜜柚中随机抽取 2 个的情况共有以下 10 种 : A 1 A 2 , A 1 B 1 , A 1 B 2 , A 1 B 3 , A 2 B 1 , A 2 B 2 , A 2 B 3 , B 1 B 2 , B 1 B 3 , B 2 B 3 , 其中质量小于 2 000 克的仅有 A 1 A 2 这 1 种情况 , 故所求概率 为 . - 17 - 考向一 考向二 考向三 考 向 四 (2) 方案 A 好 , 理由如下 : 由频率分布直方图可知 , 蜜柚质量在 [1 750,2 000) 的频率为 250 × 0 . 000 4 = 0 . 1, 同理 , 蜜柚质量在 [1 750,2 000),[2 000,2 250),[2 250,2 500),[2 500,2 750),[2 750,3 000] 的频率依次为 0 . 1,0 . 15,0 . 4,0 . 2,0 . 05 . 若按方案 A 收购 : 根据题意各段蜜柚个数依次为 500,500,750,2 000,1 000,250 . - 18 - 考向一 考向二 考向三 考 向 四 若按方案 B 收购 : ∵ 蜜柚质量低于 2 250 克的个数为 (0 . 1 + 0 . 1 + 0 . 3) × 5 000 = 1 750 蜜柚质量低于 2 250 克的个数为 5 000 - 1 750 = 3 250 . ∴ 收益为 1 750 × 60 + 3 250 × 80 = 250 × 20 × (7 × 3 + 13 × 4) = 365 000 元 . ∴ 方案 A 的收益比方案 B 的收益高 , 应该选择方案 A. - 19 - 考向一 考向二 考向三 考 向 四 频率分布直方图与古典概型的综合 例 3 为了解初三某班级的第一次中考模拟考试的数学成绩情况 , 从该班级随机调查了 n 名学生 , 数学成绩的频率分布直方图以及成绩在 100 分以上的茎叶图如图所示 . - 20 - 考向一 考向二 考向三 考 向 四 (1) 通过以上样本数据来估计这个班级模拟考试数学的平均成绩 ( 同一组中的数据用该组区间的中点值作代表 ); (2) 从数学成绩在 100 分以上的学生中任选 2 人进行学习经验交流 , 求有且只有一人成绩是 105 分的概率 . - 21 - 考向一 考向二 考向三 考 向 四 解题心得 用列举法求古典概型的基本事件 : 列举法就是把要数的对象一一列举出来分析求解的方法 . 在求古典概型的概率时 , 常常应用列举法找出基本事件数及所求事件包含的基本事件数 . 列举的方法通常有直接分类列举、列表、画树形图等 . - 22 - 考向一 考向二 考向三 考 向 四 对点训练 3 某学校为了了解本校高一学生每周课外阅读时间 ( 单位 : 小时 ) 的情况 , 按 10% 的比例对该校高一 600 名学生进行抽样统计 , 将样本数据分为 5 组 : 第一组 [0,2), 第二组 [2,4), 第三组 [4,6), 第四组 [6,8), 第五组 [8,10], 并将所得数据绘制成如图所示的频率分布直方图 . - 23 - 考向一 考向二 考向三 考 向 四 (1) 求图中的 x 的值 ; (2) 估计该校高一学生每周课外阅读的平均时间 ; (3) 为了进一步提高本校高一学生对课外阅读的兴趣 , 学校准备选拔 2 名学生参加全市阅读知识竞赛 , 现决定先在第三组、第四组、第五组中用分层抽样的方法 , 共随机抽取 6 名学生 , 再从这 6 名学生中随机抽取 2 名学生代表学校参加全市竞赛 , 在此条件下 , 求第三组中恰有一名学生被抽取的概率 . - 24 - 考向一 考向二 考向三 考 向 四 解 (1) 由题设可知 ,2 × (0 . 150 + 0 . 200 +x+ 0 . 050 + 0 . 025) = 1, 解得 x= 0 . 075 . (2) 估计该校高一学生每周课外阅读的平均时间 为 = 1 × 0 . 3 + 3 × 0 . 4 + 5 × 0 . 15 + 7 × 0 . 1 + 9 × 0 . 05 = 3 . 40( 小时 ) . (3) 由题意知 , 从第三组、第四组、第五组中依次分别抽取 3 名学生、 2 名学生和 1 名学生 . 设第三组抽到的 3 名学生是 A 1 ,A 2 ,A 3 , 第四组抽到的学生是 B 1 ,B 2 , 第五组抽到的学生是 C 1 , 则所有结果组成的基本事件空间为 Ω = {(A 1 ,A 2 ),(A 1 ,A 3 ),(A 2 ,A 3 ),(A 1 ,B 1 ),(A 1 ,B 2 ),(A 1 ,C 1 ),(A 2 ,B 1 ),(A 2 ,B 2 ),(A 2 ,C 1 ),(A 3 ,B 1 ),(A 3 ,B 2 ),(A 3 ,C 1 ),(B 1 ,B 2 ),(B 1 ,C 1 ),(B 2 ,C 1 )}, 共由 15 个基本事件组成 , 设 “ 第三组中恰有一名学生被抽取 ” 为事件 A , 则 A 中有 9 个基本事件 , 故第三组中恰有一名学生被抽取的 概率 - 25 - 考向一 考向二 考向三 考向四 独立性检验与古典概型的综合 例 4 (2018 河南郑州三模 , 文 18) 在 2018 年 3 月郑州第二次模拟考试中 , 某校共有 100 名文科学生参加考试 , 其中语文考试成绩低于 130 的占 95%, 数学成绩的频率分布直方图如图 : - 26 - 考向一 考向二 考向三 考向四 (1) 如果成绩不低于 130 的为特别优秀 , 这 100 名学生中本次考试语文、数学成绩特别优秀的大约各多少人 ? (2) 如果语文和数学两科都特别优秀的共有 3 人 . ① 从 (1) 中的这些同学中随机抽取 2 人 , 求这两人两科成绩都优秀的概率 . ② 根据以上数据 , 完成 2 × 2 列联表 , 并分析是否有 99% 的把握认为语文特别优秀的同学数学也特别优秀 . - 27 - 考向一 考向二 考向三 考向四 - 28 - 考向一 考向二 考向三 考向四 解 (1) 我校共有 100 名文科学生参加考试 , 其中语文考试成绩低于 130 的占 95%, 语文成绩特别优秀的概率为 P 1 = 1 - 0 . 95 = 0 . 05, 语文成绩特别优秀的同学有 100 × 0 . 05 = 5 人 , 数学成绩特别优秀的概率为 P 2 = 0 . 002 × 20 = 0 . 04, 数学成绩特别优秀的同学有 100 × 0 . 04 = 4 人 . (2) 语文和数学两科都优秀的有 3 人 , 单科优秀的有 3 人 , ① 记两科都优秀的 3 人分别为 A 1 , A 2 , A 3 , 单科优秀的 3 人分别为 B 1 , B 2 , B 3 , 从中随机抽取 2 人 , 共有 :( A 1 , A 2 ),( A 1 , A 3 ),( A 2 , A 3 ),( B 1 , B 2 ),( B 1 , B 3 ),( B 2 , B 3 ),( A 1 , B 1 ),( A 1 , B 2 ),( A 1 , B 3 ),( A 2 , B 1 ),( A 2 , B 2 ),( A 2 , B 3 ),( A 3 , B 1 ),( A 3 , B 2 ),( A 3 , B 3 ) 共 15 种 , 其中这两人成绩都优秀的有 ( A 1 , A 2 ),( A 1 , A 3 ),( A 2 , A 3 )3 种 , 则这两人两科成绩都优秀的概率 为 - 29 - 考向一 考向二 考向三 考向四 - 30 - 考向一 考向二 考向三 考向四 解题心得 1 . 古典概型是基本事件个数有限 , 每个基本事件发生的概率相等的一种概率模型 , 计算概率时 , 要先判断再计算 . 2 . 独立性检验的步骤 : 列表、计算、检验 . - 31 - 考向一 考向二 考向三 考向四 对点训练 4 某研究性学习小组调查研究 “ 中学生使用智能手机对学习的影响 ”, 部分统计数据如下表 : - 32 - 考向一 考向二 考向三 考向四 (1) 试根据以上数据 , 运用独立性检验思想 , 指出有多大把握认为中学生使用智能手机对学习有影响 ? (2) 研究小组将该样本中使用智能手机且成绩优秀的 4 名同学记为 A 组 , 不使用智能手机且成绩优秀的 8 名同学记为 B 组 , 计划从 A 组推选的 2 人和 B 组推选的 3 人中 , 随机挑选 2 人在学校升旗仪式上作 “ 国旗下讲话 ” 分享学习经验 . 求挑选的 2 人恰好分别来自 A,B 两组的概率 . - 33 - 考向一 考向二 考向三 考向四 解 (1 ) . 因为 7 . 879