高中数学选修2-1公开课课件3_1_4空间向量的正交分解及其坐标表示 18页

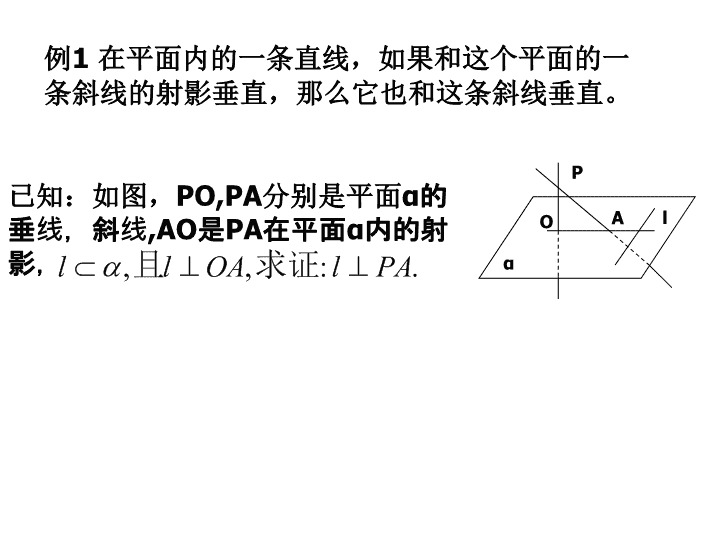
3.1.4 空间向量的正交分 解及其坐标表示 l α O P 例 1 在平面内的一条直线，如果和这个平面的一条斜线的射影垂直，那么它也和这条斜线垂直。 已知：如图， PO,PA 分别是平面 α 的垂线，斜线 ,AO 是 PA 在平面 α 内的射影， A l α O P A 已知：如图， PO,PA 分别是平面 α 的垂线，斜线 ,AO 是 PA 在平面 α 内的射影， a 分析 : 同样可用向量 , 证明思路几乎一样 , 只不过其中的加法运算用减法运算来分析 . α n l m g n z m g l 例 2 如图， m,n 是平面 α 内的两条相交直线。如果 l ⊥ m,l ⊥ n, 求证： l ⊥ α 3.1.4 空间向量的正交分 解及其坐标表示 共线向量定理 : 复习： 共面向量定理 : 平面向量基本定理： 平面向量的正交分解及坐标表示 x y o 问题： 我们知道，平面内的任意一个向量 都可以用两个不共线的向量 来表示（平面向量基本定理）。对于空间任意一个向量，有没有类似的结论呢？ x y z O Q P 由此可知，如果 是空间两两垂直的向量，那么，对空间任一向量 ，存在一个有序实数组 {x,y,z} 使得 我们称 为向量 在 上的分向量。 探究： 在空间中，如果用任意三个不共面向量 代替两两垂直的向量 ，你能得出类似的 结论吗？ 任意不共面的三个向量都可做为空间的一个基底。 空间向量基本定理： 如果三个向量 不共面，那么对空间任一向量 ，存在一个唯一的有序实数组 x ， y ， z ，使 都叫做 基向量 （ 1 ）任意不共面的三个向量都可做为空间的一个基底。 特别提示： 对于基底 { a,b,c }, 除了应知道 a,b,c 不共面， 还应明确： （ 2 ） 由于可视 为与任意一个非零向量共线，与任意两个非零向量共面，所以三个向量不共面，就隐含着它们都不是 。 （ 3 ）一个基底是指一个向量组，一个基向量是指基底中的某一个向量，二者是相关连的不同概念。 推论： 设 O 、 A 、 B 、 C 是不共线的四点，则对空间任一点 P ，都存在唯一的有序实数组 {x,y,z} ，使 当且仅当 x+y+z=1 时， P 、 A 、 B 、 C 四点共面。 一、空间直角坐标系 单位正交基底： 如果空间的一个基底的三个基向量互相垂直，且长都为 1 ，则这个基底叫做 单位正交基底 , 常用 e 1 , e 2 , e 3 表示 空间直角坐标系： 在空间选定一点 O 和一个单位正交基底 e 1 ,e 2 ,e 3 , 以点 O 为原点，分别以 e 1 ,e 2 ,e 3 的正方向建立三条数轴： x 轴、 y 轴、 z 轴，它们都叫做坐标轴 . 这样就建立了一个空间直角坐标系 O--xyz 点 O 叫做原点，向量 e 1 ,e 2 ,e 3 都叫做 坐标向量 . 通过每两个坐标轴的平面叫做 坐标平面 。 给定一个空间坐标系和向量 , 且设 e 1 ,e 2 ,e 3 为坐标向量，由空间向量基本定理，存在唯一的有序实数组 (x,y, z) 使 p = xe 1 +ye 2 +ze 3 有序数组 ( x, y, z) 叫做 p 在空间直角坐标系 O--xyz 中的坐标，记作 .P=(x,y,z) 二、空间向量的直角坐标系 x y z O e 1 e 2 e 3 在空间直角坐标系 O--xyz 中，对空间任一点， A, 对应一个向量 OA ，于是存在唯一的有序实数组 x,y,z ，使 OA=xe 1 +ye 2 +ze 3 在单位正交基底 e 1 , e 2 , e 3 中与向量 OA 对应的有序实数组 (x,y,z) ，叫做点 A 在此空间直角坐标系中的坐标，记作 A(x,y,z) ，其中 x 叫做点 A 的横坐标， y 叫做点 A 的纵坐标， z 叫做点 A 的竖坐标 . x y z O A(x,y,z) e 1 e 2 e 3 练习： 1 、在空间坐标系 o-xyz 中， ( 分别是与 x 轴、 y 轴、 z 轴的正方向相同的单位向量 ) 则 的坐标为 . 2 、点 M （ 2 ， -3 ， -4 ）在坐标平面 xoy 、 xoz 、 yoz 内的正投影的坐标分别为 ，关于原点的对称点为 ，关于轴的对称点为 ， 例题 已知空间四边形 OABC ，其对角线为 OB ， AC ， M ， N ，分别是对边 OA ， BC 的中点，点 P ， Q 是线段 MN 三等分点，用基向量 OA ， OB ， OC 表示向量 OP,OQ. B O A C P N M Q 1 、已知向量 {a ， b ， c} 是空间的一个基底． 求证：向量 a+b ， a-b ， c 能构成空间的一个基底． 练习 练习 2