高中数学选修2-1公开课课件3_1_5空间向量运算的坐标表示 21页

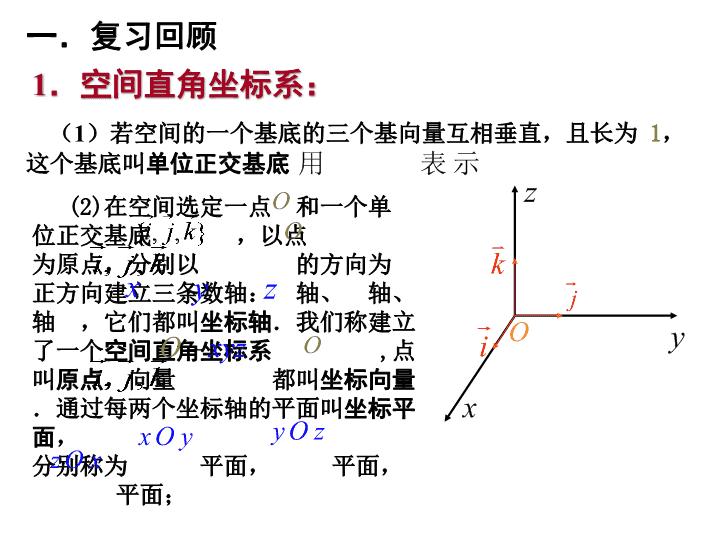
3.1.5 空间向量运算的 坐标表示 1 ．空间向量的基本定理： 2 ．平面向量的坐标表示及运算律： 一．复习回顾 若是 空间的一个基底， 是空间任意一向量，存在唯一的实数组使． 1 ．空间直角坐标系： （ 1 ）若空间的一个基底的三个基向量互相垂直，且长为 1 ， 这个基底叫 单位正交基底 (2) 在空间选定一点 和一个单位正交基底 ，以点 为原点，分别以 的方向为正方向建立三条数轴： 轴、 轴、 轴 ，它们都叫 坐标轴 ．我们称建立了一个 空间直角坐标系 , 点 叫 原点 ，向量 都叫 坐标向量 ．通过每两个坐标轴的平面叫 坐标平面 ， 分别称为 平面， 平面， 平面； 一．复习回顾 （ 4 ）在空间直角坐标系中，让右手拇指指向 轴的正方向，食指指向 轴的正方向，如果中指指向 轴的正方向，称这个坐标系为 右手直角坐标系 。本书建立的坐标系都是右手直角坐标系 . （ 3 ）作空间直角坐标系 时，一般使 2 ．空间直角坐标系中的坐标： 如图给定空间直角坐标系和向量 ，设 为坐标向量 , 则存在唯一的有序实数组 ，使 ， 有序实数组 叫作向量 在空间直角坐标系 中的坐标，记作 ． 在空间直角坐标系 中，对空间任一点 ，存在唯一的有序实数组 ，使 ，有序实数组 叫作向量 在 空间直角坐标系 中的 坐标 ， 记作 ， 叫 横坐标 ， 叫 纵坐标 ， 叫 竖坐标 ． 一、向量的直角坐标运算 新课 1. 距离公式 （ 1 ）向量的长度（模）公式 注意：此公式的几何意义是表示长方体的对角线的长度。 二、距离与夹角 在空间直角坐标系中，已知　　　　　　、 　　　　，则 （ 2 ）空间两点间的距离公式 2. 两个向量夹角公式 注意： 　（ 1 ）当　　　　　　 时，　　　同向； 　（ 2 ）当　　　　　　 时，　　　反向； 　（ 3 ）当　　　　　　 时，　　　。 思考：当　　　　　　 及 　　 时，夹角在什么范围内？ 例 1 ．已知 解 : 三、应用举例 三、应用举例 例 2 　已知　　　　、　　　　，求： 　（ 1 ）线段　　的中点坐标和长度；　 解：设　　　　　是　　的中点，则 ∴ 点　的坐标是　　　　　 . 　 （ 2 ）到　　　两点距离相等的点　　　　　的 坐标　　　　满足的条件。 解：点　　　　到　　　的距离相等，则 化简整理，得 即到　　　两点距离相等的点的坐标　　　　满 足的条件是 解：设正方体的棱长为 1 ，如图建 立空间直角坐标系　　　　，则　 　　　 例 3 　如图 , 在正方体　　　　　　　中，　　　 　　　　　，求　　与　　所成的角的余弦值 . 　 　 证明：不妨设已知正方体的棱长为 1 个单 位长度 , 设 分别以 为坐标向量建立空间直 角坐标系 则 例 4 ． 在正方体 练习 3 已知 垂直于正方形 所在的平面 , 分别是 的中点 , 并且 , 求证 : 证明 : 分别以 为坐标向量建立空间直角坐标系 则 练习 4 ：如图，已知线段 AB⊂ α ， AC ⊥α ， BD ⊥ AB ， DE ⊥α ，∠ DBE=30 º ，如果 AB=6 ， AC=BD=8 ，求 CD 的长及异面直线 CD 与 AB 所成角的大小。 练习：平行六面体 ABCD—A 1 B 1 C 1 D 1 中， AB=4 ， AD=3 ， AA 1 =5 ，∠ BAD=∠BAA 1 =∠DAA 1 =60 º ， E 、 H 、 F 分别是 D 1 C 1 、 AB 、 CC 1 的中点。（ 1 ）求 AC 1 的长；（ 2 ）求 BE 的长；（ 3 ）求 HF 的长；（ 4 ）求 BE 与 HF 所成角的大小。 10 证明 : 设正方体的棱长为 1, 建立如图的空间直角坐标系 x y z A 1 D 1 C 1 B 1 A C B D F E