2020届高考文科数学二轮专题复习课件：高考大题 满分规范（六） 31页

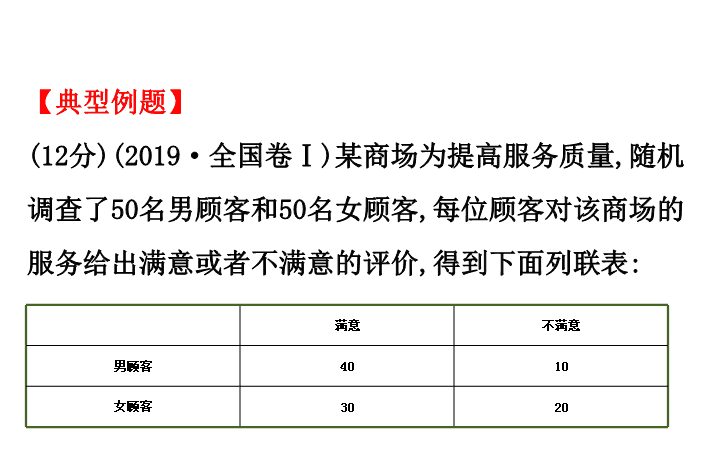
高考大题 · 满分规范（六） 统计与概率类解答题 【典型例题 】 (12 分 )(2019 · 全国卷 Ⅰ) 某商场为提高服务质量 , 随机 调查了 50 名男顾客和 50 名女顾客 , 每位顾客对该商场的 服务给出满意或者不满意的评价 , 得到下面列联表 : 满意 不满意 男顾客 40 10 女顾客 30 20 (1) 分别估算男、女顾客对该商场服务满意的概率 . (2) 能否有 95% 的把握认为男、女顾客对该商场服务的 评价有差异 ? 附 :K 2 = P(K 2 ≥k 0 ) 0.050 0.010 0.001 k 0 3.841 6.635 10.828 【题目拆解 】 本题可拆解成以下几个小问题 : (1)① 估计男顾客对该商场服务满意的概率 ; ② 估计女顾客对该商场服务满意的概率 . (2) 运用 K 2 = 公式求值 , 与临界值比较大小进行评判 . 【标准答案 】 【解析 】 (1) 由题中表格可知 ,50 名男顾客对该商场服务 满意的有 40 人 , 所以男顾客对该商场服务满意的概率估 计为 P 1 = , ………………① 50 名女顾客对该商场服务满意的有 30 人 , 所以女顾客对 该商场服务满意的概率估计为 P 2 = .…… ② (2) 由列联表可知 K 2 的观测值 k= ≈4.762>3.841, ………… ③ 所以能有 95% 的把握认为男、女顾客对该商场服务的评 价有差异 . ………… ④ 【阅卷现场 】 第 (1) 问 第 (2) 问 得 分 点 ① ② ③ ④ 3 3 4 2 6 分 6 分 第 (1) 问踩点得分说明 ① 男顾客对该商场服务满意的概率估计正确得 3 分 ; ② 女顾客对该商场服务满意的概率估计正确得 3 分 ; 第 (2) 问踩点得分说明 ③ K 2 计算正确得 4 分 ; ④ 作出判断得 2 分 . 【高考状元 · 满分心得 】 1. 概率统计问题的处理思路 概率时常与统计、统计案例相结合 , 通过各种统计图表提取有用的信息 , 并会利用最小二乘法求出回归直线方程及利用 K 2 公式求出变量的观测值是解决问题的关键 . 2. 两个分类变量 A 和 B 是否有关系的判断方法 (1) 当 K 2 ≤2.706 时 , 没有充分的证据判断变量 A,B 有关系 , 可以认为变量 A,B 没有关系 . (2) 当 K 2 >2.706 时 , 有 90% 的把握判断变量 A,B 有关系 . (3) 当 K 2 >3.841 时 , 有 95% 的把握判断变量 A,B 有关系 . (4) 当 K 2 >6.635 时 , 有 99% 的把握判断变量 A,B 有关系 . 【跟踪演练 · 感悟体验 】 1.(2019 · 北京高考 ) 改革开放以来 , 人们的支付方式发 生了巨大转变 . 近年来 , 移动支付已成为主要支付方式 之一 . 为了解某校学生上个月 A,B 两种移动支付方式的 使用情况 , 从全校所有的 1 000 名学生中随机抽取了 100 人 , 发现样本中 A,B 两种支付方式都不使用的有 5 人 , 样本中仅使用 A 和仅使用 B 的学生的支付金额分布情况如下 : 　　　　支付金额 支付方式　　　　 不大于 2 000 元 大于 2 000 元 仅使用 A 27 人 3 人 仅使用 B 24 人 1 人 (1) 估计该校学生中上个月 A,B 两种支付方式都使用的人数 . (2) 从样本仅使用 B 的学生中随机抽取 1 人 , 求该学生上个月支付金额大于 2 000 元的概率 . (3) 已知上个月样本学生的支付方式在本月没有变化 . 现从样本仅使用 B 的学生中随机抽查 1 人 , 发现他本月的支付金额大于 2 000 元 . 结合 (2) 的结果 , 能否认为样本仅使用 B 的学生中本月支付金额大于 2 000 元的人数有变化 ? 说明理由 . 【解析 】 (1) 由已知 , 样本中 , 仅使用 A 的有 27+3=30( 人 ), 仅使用 B 的有 24+1=25( 人 ), 都不使用的有 5 人 , 所以都使用的有 100-30-25-5=40( 人 ), 所以估计该校学生中上个月 A,B 两种支付方式都使用的 人数为 1 000× =400( 人 ). (2) 样本中仅使用 B 的有 25 人 , 其中支付金额大于 2 000 元的有 1 人 , 所以该学生上个月支付金额大于 2 000 元的概率为 . (3) 参考答案 1: 不能认为样本仅使用 B 的学生中本月支付金额大于 2 000 元的人数有变化 . 若人数没有变化 , 则样本中仅使用 B 的学生有 25 人 , 支付金额大于 2 000 元的有 1 人 , 由 (2) 知 , 随机抽取 1 人 , 支付金额大于 2 000 元的概率 为 , 虽然此事件是小概率事件 , 但也有发生的可能性 . 这体 现了概率的随机性 . 参考答案 2: 可以认为样本仅使用 B 的学生中本月支付金额大于 2 000 元的人数有变化 . 若人数没有变化 , 则样本中仅使用 B 的学生有 25 人 , 支付金额大于 2 000 元的有 1 人 , 由 (2) 知 , 随机抽取 1 人 , 支付金额大于 2 000 元的概率 为 , 此事件发生的可能性很小 , 所以认为有变化 . 2.(2019 · 长春模拟 ) 到 2020 年 , 我国将全面建立起新的 高考制度 , 新高考采用 3+3 模式 , 其中语文、数学、英语 三科为必考科目 , 满分各 150 分 , 另外考生还要依据想考 取的高校及专业的要求 , 结合自己的兴趣、爱好等因素 , 在思想政治、历史、地理、物理、化学、生物 6 门科目 中自选 3 门 (6 选 3) 参加考试 , 满分各 100 分 . 为了顺利迎接新高考改革 , 某学校采用分层抽样的方法从高一年级 1 000 名 ( 其中男生 550 名 , 女生 450 名 ) 学生中抽取了 n 名学生进行调查 . (1) 已知抽取的 n 名学生中有女生 45 名 , 求 n 的值及抽取的男生的人数 . (2) 该校计划在高一上学期开设选修中的“物理”和“地理”两个科目 , 为了解学生对这两个科目的选课情况 , 对在 (1) 的条件下抽取到的 n 名学生进行问卷调查 ( 假定每名学生在这两个科目中必须选择一个科目 , 且只能选择一个科目 ), 得到如下 2×2 列联表 . 选择“物理” 选择“地理” 总计 男生 10 女生 25 总计 ① 请将列联表补充完整 , 并判断是否有 99% 以上的把握 认为选择科目与性别有关系 . ② 在抽取的选择“地理”的学生中按性别分层抽样抽 取 6 名 , 再从这 6 名学生中抽取 2 名 , 求这 2 名中至少有 1 名 男生的概率 . P(K 2 ≥k 0 ) 0.05 0.01 k 0 3.841 6.635 附 :K 2 = , 其中 n=a+b+c+d . 【解析 】 (1) 由题意得 , 解得 n=100, 则抽取的男生的人数为 550× =55. (2)① 选择“物理” 选择“地理” 总计 男生 45 10 55 女生 25 20 45 总计 70 30 100 则 K 2 的观测值 k= ≈8.128 9>6.635, 所以有 99% 以上的把握认为选择科目与性别有关系 . ② 由题易知抽取的选择“地理”的 6 名学生中 , 有 2 名男 生 , 分别记为 A,B,4 名女生 , 分别记为 a,b,c,d . 从 6 名学生中随机抽取 2 名 , 有 AB,Aa,Ab,Ac,Ad,Ba,Bb , Bc,Bd,ab,ac,ad,bc,bd,cd 共 15 种情况 , 其中至少有 1 名 男生的有 AB,Aa,Ab,Ac,Ad,Ba,Bb,Bc,Bd 共 9 种情况 , 故所求概率为 .